python 实现参数估计--置信区间
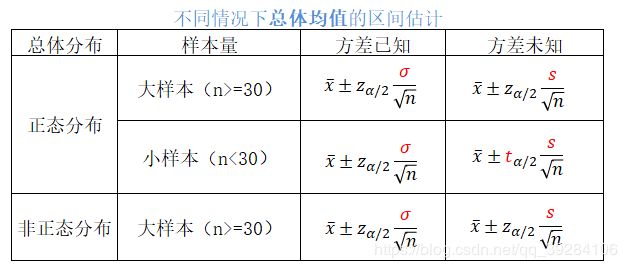
(1)py实现一个总体均值的置信区间
def mean_interval(mean=None, std=None, sig=None, n=None, confidence=0.95):
"""
mean:样本均值
std:样本标准差
sig: 总体方差
n: 样本量
confidence:置信水平
功能:构建总体均值的置信区间
"""
alpha = 1 - confidence
z_score = scipy.stats.norm.isf(alpha / 2) # z分布临界值
t_score = scipy.stats.t.isf(alpha / 2, df = (n-1) ) # t分布临界值
if n >= 30 and sig != None:
me = z_score*sig / np.sqrt(n) # 误差
lower_limit = mean - me
upper_limit = mean + me
if n >= 30 and sig == None:
me = z_score*std / np.sqrt(n)
lower_limit = mean - me
upper_limit = mean + me
if n < 30 and sig == None:
me = t_score*std / np.sqrt(n)
lower_limit = mean - me
upper_limit = mean + me
return (round(lower_limit, 3), round(upper_limit, 3))
mean_interval(mean=8900, std=None, sig=500, n=35, confidence=0.95)
mean_interval(mean=8900, std=500, sig=None, n=35, confidence=0.90)
mean_interval(mean=8900, std=500, sig=None, n=35, confidence=0.99)
(2)py实现一个总体方差的置信区间
(1) 样本均值为21, 样本标准差为2, 样本量为50;
(2) 样本均值为1.3, 样本标准差为0.02, 样本量为15;
(3) 样本均值为167, 样本标准差为31, 样本量为22;
Question1: 根据以上样本结果,计算总体方差的90%的置信区间?
Question2: 根据以上样本结果,计算总体标准差的90%的置信区间?
def std_interval(mean=None, std=None, n=None, confidence=0.95, para="总体标准差"):
"""
mean:样本均值
std:样本标准差
n: 样本量
confidence:置信水平
para:总体估计参数
功能:构建总体方差&总体标准差的置信区间
"""
variance = np.power(std,2)
alpha = 1 - confidence
chi_score0 = scipy.stats.chi2.isf(alpha / 2, df = (n-1))
chi_score1 = scipy.stats.chi2.isf(1 - alpha / 2, df = (n-1))
if para == "总体标准差":
lower_limit = np.sqrt((n-1)*variance / chi_score0)
upper_limit = np.sqrt((n-1)*variance / chi_score1)
if para == "总体方差":
lower_limit = (n-1)*variance / chi_score0
upper_limit = (n-1)*variance / chi_score1
return (round(lower_limit, 2), round(upper_limit, 2))
std_interval(mean=21, std=2, n=50, confidence=0.90)
std_interval(mean=1.3, std=0.02, n=15, confidence=0.90)
std_interval(mean=167, std=31, n=22, confidence=0.90) (3)py实现两个总体方差比的置信区间
data1 = [3.45, 3.22, 3.90, 3.20, 2.98, 3.70, 3.22, 3.75, 3.28, 3.50, 3.38, 3.35, 2.95, 3.45, 3.20, 3.16, 3.48, 3.12, 3.20, 3.18, 3.25]
data2 = [3.22, 3.28, 3.35, 3.38, 3.19, 3.30, 3.30, 3.20, 3.05, 3.30, 3.29, 3.33, 3.34, 3.35, 3.27, 3.28, 3.16, 3.28, 3.30, 3.34, 3.25]
def two_std_interval(d1, d2, confidence=0.95, para="两个总体方差比"):
"""
d1: 数据1
d2: 数据2
confidence:置信水平
para:总体估计参数
功能:构建两个总体方差比&总体标准差比的置信区间
"""
n1 = len(d1)
n2 = len(d2)
var1 = np.var(d1, ddof=1) # ddof=1 样本方差
var2 = np.var(d2, ddof=1) # ddof=1 样本方差
alpha = 1 - confidence
f_score0 = scipy.stats.f.isf(alpha / 2, dfn=n1-1, dfd=n2-1) # F分布临界值
f_score1 = scipy.stats.f.isf(1-alpha / 2, dfn=n1-1, dfd=n2-1) # F分布临界值
if para == "两个总体标准差比":
lower_limit = np.sqrt((var1 / var2) / f_score0)
upper_limit = np.sqrt((var1 / var2) / f_score01)
if para == "两个总体方差比":
lower_limit = (var1 / var2) / f_score0
upper_limit = (var1 / var2) / f_score1
return (round(lower_limit, 2), round(upper_limit, 2))
two_std_interval(data1, data2, confidence=0.95, para="两个总体方差比")