机器学习(无监督学习)关联规则Apriori算法原理与python实现
一、关联规则原理:
1、概述:
关联规则算法是在一堆数据集中寻找数据之间的某种关联,通过该算法我们可以对数据集做关联分析——在大规模的数据中寻找有趣关系的任务。这些关系可以有两种形式:频繁项集、关联规则。
- 频繁项集:经常出现在一块的物品的集合。
- 关联规则:暗示两种物品之间可能存在很强的关系。
关联分析典型的例子,沃尔玛超市啤酒于尿不湿的关联分析。例如:购物篮数据
| 订单编号 | 购买商品集合 |
| 001 | 羽毛球拍,羽毛球 |
| 002 | 羽毛球,球网,纸巾,矿泉水 |
| 003 | 羽毛球拍,球网,纸巾,红牛 |
| 004 | 羽毛球,羽毛球拍,球网,纸巾 |
| 005 | 羽毛球,羽毛球拍,球网,红牛 |
名词定义:
- 事物:每一个订单被称为一个事物,上表包含5个事物;
- 项:订单中的每一个物品被称为一个项;
- 项集:包含0个或多个项的集合被称为项集,如:{羽毛球拍,羽毛球};
- k-项集:包含k个项的项集被称为K项集,如{羽毛球拍,羽毛球}称为2-项集;
- 前件与后件:对于规则{羽毛球拍}-->{羽毛球},{羽毛球拍}叫做前件,{羽毛球}叫做后件。
2、频繁项集的评估标准:
频繁项集:经常出现在一块的物品的集合,当数据量非常大的时候,我们不可能通过人工去算,所以催生了关联规则的算法,如:Apriori、prefixSpan、CBA等。有了计算方法,那么常常出现在一块多少次的物品集合才算频繁项集,则还需要一个评估频繁项集的标准。评估标准有支持度,置信度、和提升度等,需要自定义一个阈值来衡量判别。
- 支持度(support):几个关联的数据集中出现的次数占总数据集的比重,或者说几个数据关联出现的概率。上例中:Support(羽毛球,球网,纸巾)= 2/5.。一般来说支持度高不一定是频繁项集,但支持度低一定不能构成频繁项集,所以可设定一个最低的支持度来进行过滤。
- 置信度(confidence):一个数据出现后,另一个数据出现的概率,或者说是数据的条件概率。定量评估一个频繁项集的置信度(即准确度)的统计量。Confidence(y-->x)=P(X|Y)=P(XY)/P(Y)。针对如{羽毛球拍}->{羽毛球}这样的关联规则来定义的。计算为 支持度{羽毛球拍,羽毛球}/支持度{羽毛球拍},其中{羽毛球拍,羽毛球}的支持度为3/5,{羽毛球拍}的支持度为4/5,所以“羽毛球拍->羽毛球”的置信度为3/4=0.75,这意味着羽毛球拍的记录中,我们的规则有75%都适用。从关联规则的可信程度角度来看,“购买羽毛球拍的顾客会购买羽毛球”这个商业推测,有75%的可能性是成立的,也可以理解为做这种商业决策,可以获得75%的回报率期望。同理:Confidence(yz-->x)=p(x|yz)=p(xyz)/p(yz)。
- 提升度(lift):表示含有Y的条件下同时含有X的概率,与x总体发生的概率之比,也就是说x对y的提升度与x总体发生的概率之比,即Lift(y-->x)=p(x|y)/p(x)=Confidence(y-->x)/p(x)。提升度大于1 有效的强关联规则,小于1 无效的强关联规则,等于1 x与y独立。
3.关联规则发现
给定事务的集合T,关联规则发现是指找出支持度大于等于阈值,并且置信度大于等于阈值的所有规则。挖掘关联规则的一种原始方法是:计算每个可能规则的支持度和置信度,但可以从数据集提取的规则的数目达指数级,更具体地说,从包含d个项的数据集提取的可能规则的总数为:![]() 。上面的案例中就有3^6-2^7+1种可能的关联规则。
。上面的案例中就有3^6-2^7+1种可能的关联规则。
当数据量增加的时候,计算非常庞大,所以往往我们会采取剪枝策略,即设定支持度、置信度的阈值,没有达到阈值的项集将不必再进行后续的计算。
于是将关联规则分为2个主要的子任务:
- 1.频繁项集的产生:发现满足最小支持度阈值的所有项集,把这些项集称作频繁项集。
- 2.规则 的产生:从频繁项集中提取高置信度的规则,把这些规则称作强规则。
优化计算开销:通常频繁项集的产生计算开销远远大于规则产生所需要的计算开销。
- 1.减少候选项集数目M。
- 2.减少比较次数。替代将每个候选项集与每个事物相匹配,可以使用更高级的数据结构,或者存储候选项集或者压缩数据集,来减少比较次数。具体体现看Apriori算法。
二、Apriori算法
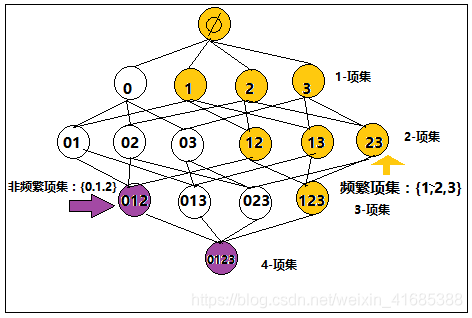
先验原理:如果一个项集是频繁的,则它的所有子集一定也是频繁的。如果一个项集是非频繁的,则它的所有超集都是非平凡的。这样找到一个非频繁项集后,就可以把它的超集进行剪枝处理了。
如下图,假如0,1,2,3分别表示4类商品,其中我们假定123为频繁项集,则12,13,23,1,2,3都是频繁的。
反而言之,如果012是非频繁项集,那么他的超集0123也是非频繁的。
Apriori算法过程:
- 1、数据集-->设定最低支持度阈值-->获取1-项集-->过滤出频繁项集(剪枝非频繁)-->获取2-项集-->过滤出频繁项集(剪枝非频繁)--->......
- 2、设定置信度阈值-->从频繁项集中提取高置信度的规则
三、代码案例
# pip install apriori
# pip install MLxtend
import pandas as pd
import xlrd
from mlxtend.frequent_patterns import apriori
from mlxtend.frequent_patterns import association_rules
import warnings
warnings.filterwarnings("ignore") #用于排除警告#读取sheet_name='table1'的数据
df=pd.read_excel('e:\glgz.xlsx') #根据表的名称
display(df)#默认读取前5行的数据| 订单编号 | 面膜 | 洗面奶 | 美白霜 | 补水霜 | 洁面乳 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 2 | 0 | 1 | 1 | 1 | 1 |
| 2 | 3 | 0 | 0 | 0 | 1 | 1 |
| 3 | 4 | 1 | 1 | 0 | 1 | 0 |
| 4 | 5 | 1 | 0 | 1 | 0 | 1 |
| 5 | 6 | 1 | 1 | 1 | 1 | 1 |
| 6 | 7 | 1 | 0 | 0 | 0 | 0 |
| 7 | 8 | 0 | 0 | 1 | 1 | 1 |
| 8 | 9 | 1 | 1 | 0 | 1 | 1 |
# 调用apriori算法,并且设定最小支持度
frequent_itemsets = apriori(df[['面膜', '洗面奶', '美白霜', '补水霜', '洁面乳' ]],min_support=0.4, use_colnames=True)
# frequent_itemsets = apriori(df.drop("订单编号",1),min_support=0.4,use_colnames=True)
display(frequent_itemsets)# 生成关联规则二维表,min_threshold=1表示最少是两种产品的关联规则
rules = association_rules(frequent_itemsets,metric="lift",min_threshold=1)
display(rules)注意:antecedent support:前置支持度(由前面一个产品到后面一个产品的支持度);consequent support:后置支持度(由后面一个产品到前面一个产品的支持度);support:综合支持度;confidence:置信度;lift:提示度。
其中support太小的话,则表示该关联规则在整体样本中出现的概率较低,对整体来说分析价值会降低(整体贡献度不够);confidence太低,则说明该组产品组合的价值不高,没有组合价值;lift提升度大于1 有效的强关联规则,小于1 无效的强关联规则,等于1 x与y独立。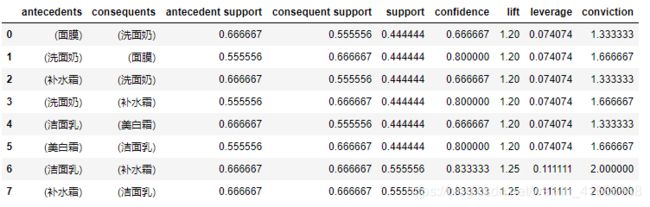
#筛选出提升度和置信度满足条件的关联规则
rules[ ( rules["lift"] > 1) & (rules["confidence"] > 0.8) ]结论:在支持度大于等于0.4,置信度大于0.8且提升度大于1的条件下,关联产品组合有洁面乳和补水霜,且是双侧关联。即可以将这两个产品进行组合售卖,会提高收益。