Java 求最大公约数（欧几里德算法证明）

基本概念

如果数a能被数b整除，a就叫做b的倍数，b就叫做a的约数。

几个整数中公有的约数，叫做这几个数的公约数；其中最大的一个，叫做这几个数的最大公约数（greatest common divisor）。

 

代码示例

1.使用循环

public static int getGCD(int a, int b) {
    if (a < 0 || b < 0) {
        return -1; // 数学上不考虑负数的约数
    }
    if (b == 0) {
        return a;
    }
    while (a % b != 0) {
        int temp = a % b;
        a = b;
        b = temp;
    }
    return b;
}

 

2.使用递归

public static int getGCD(int a, int b) {
    if (a < 0 || b < 0) {
        return -1; // 数学上不考虑负数的约数
    }
    if (b == 0) {
        return a;
    }
    return a % b == 0 ? b : getGCD(b, a % b);
}

 

欧几里德算法证明：（下述内容仅做了解）

上面代码使用的是欧几里德算法，又称辗转相除法。

假设有非零正整数 A、B，其中 A > B，将 A 减 B 记为 C，即 A - B = C。

最大公约数记为 GCD（greatest common divisor），例如 A、B 的最大公约数记为 GCD(A, B)。

 

求证：GCD(A, B) = GCD(B, R)

（其中 R 为 A 除以 B 的余数，或记为 R = A - n * B，n 为 A 除以 B 的商。即 R = A % B）

 

第一步：证明 GCD(A, B) 能够整除 C

1.因为 GCD(A, B) 是 A 的公约数，存在整数 X，使得 X * GCD(A, B) = A；

2.因为 GCD(A, B) 是 B 的公约数，存在整数 Y，使得 Y * GCD(A, B) = B；

3.因为 A - B = C，即

X * GCD(A, B) - Y * GCD(A, B) = C

(X - Y) * GCD(A, B) = C

使用图片表示即：

所以有结论：

GCD(A, B) 不仅是 A 和 B 的最大公约数，同时也是 C 的约数。

 

第二步：证明 GCD(B, C) 能够整除 A

1.因为 GCD(B, C) 是 B 的公约数，存在整数 M，使得 M * GCD(B, C) = B；

2.因为 GCD(B, C) 是 C 的公约数，存在整数 N，使得 N * GCD(B, C) = C；

3.因为 B + C = A，即

M * GCD(B, C) + N * GCD(B, C) = A

(M + N) * GCD(B, C) = A

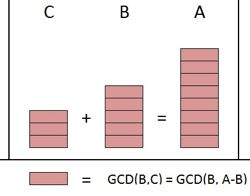
使用图片表示即：

所以有结论：

GCD(B, C) 不仅是 B 和 C 的最大公约数，同时也是 A 的约数。

 

第三步：证明 GCD(A, B) = GCD(B, C)

1.因为 GCD(A, B) 是 A 和 B 的最大公约数，同时也是 C 的约数，所以 GCD(A, B) 一定也是 B 和 C 的约数。由于 GCD(B, C) 是 B 和 C 的最大公约数，所以存在

GCD(A, B) <= GCD(B, C)

2.因为 GCD(B, C) 是 B 和 C 的最大公约数，同时也是 A 的约数，所以 GCD(B, C) 一定也是 A 和 B 的约数。由于 GCD(A, B) 是 A 和 B 的最大公约数，所以存在

GCD(B, C) <= GCD(A, B)

3.由上可得 GCD(A, B) = GCD(B, C)

使用图片表示即：

 

第四步：证明 GCD(A, B) = GCD(B, R)

1.因为 GCD(A, B) = GCD(B, C)，即 GCD(A, B) = GCD(B, A - B)

2.上式也可记为 GCD(A, B) = GCD(A - B, B)

3.重复上一步，即有

GCD(A, B) = GCD(A - B, B) = GCD(A - 2B, B) = ... = GCD(A - n * B, B)

4.所以 GCD(A, B) = GCD(B, R)