使用NuSMV解决过河问题

使用NuSMV做形式化验证

NuSMV的安装

在 http://nusmv.fbk.eu/bin/bin_download2-v2.cgi 页面下载合适的二进制可运行版本即可。

在本报告中，本人下载了 http://nusmv.fbk.eu/distrib/NuSMV-2.6.0-win64.tar.gz 文件。

解压后，即可得到具有如下目录的文件夹：

在bin目录下有可执行文件nusmv.exe，直接在命令行运行即可。

当然，为了方便起见，也可以将NuSMV.exe所在的目录添加到系统的环境变量中，这样就可以在系统的任意工作目录使用NuSMV。

使用NuSMV解决过河问题

过河问题的描述

一个人带着狼、山羊和白菜在一条河的左岸，有一条船，大小正好能装下这个人和其它三者之一，人和他的随行物都要带过岸，但他每次只能带一样东西摆渡过河。如人将狼和羊留在同一岸，无人照顾，那么狼会把羊吃掉。同样，如羊和白菜在同一岸，无人照顾，那么羊会吃了白菜。找出一种运输方案，使得这些东西能够安全运输到对岸。

画出过河问题的有限状态机

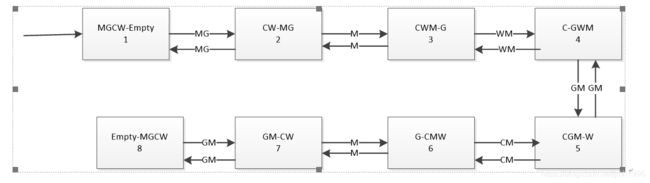
其中MGCW-Empty表示初始状态。“—”左边的符号表示对应的符号在左岸。“—”右边的服务表述对应的符号在右岸。

M表示人，G表示羊goat,C表示白菜Cabbage,W表示狼wolf.
箭头表示表示每次在船上运输什么东西。

使用NuSMV表示出过河问题的状态机

MODULE main
VAR
	ferrymen:boolean;
	goat:boolean;
	wolf:boolean;
	cabbage:boolean;
	ship:{goat_man,wolf_man,cabbage_man,empty,man};
	--ship 表示船上装着是什么
ASSIGN
	init(ferrymen):=FALSE;	--人在左边
	init(goat):=FALSE;		--羊在左边
	init(wolf):=FALSE;		--狼在左边
	init(cabbage):=FALSE;	--白菜在左边
	init(ship):=empty;		--船上为空
							--初始化的时候,全部在河岸的左边FALSE
ASSIGN
	next(ship):=	
		case
			ferrymen=TRUE&ferrymen=goat & goat=wolf & goat=cabbage :empty;			--全部已经过河,不再运输
			ferrymen=FALSE & goat=FALSE & wolf=FALSE & cabbage=FALSE : {goat_man};	--表示状态1的转移关系
			ferrymen=TRUE&goat=TRUE & cabbage=FALSE & wolf=FALSE :{goat_man,man};	--表示状态2的转移关系
			ferrymen=FALSE & cabbage=FALSE&wolf=FALSE&goat=TRUE : {man,wolf_man};	--表示状态3的转移关系
			ferrymen=TRUE & cabbage=FALSE & wolf=TRUE&goat=TRUE : {goat_man,wolf_man};	--表示状态4的转移关系
			ferrymen=FALSE & cabbage=FALSE & wolf=TRUE&goat=FALSE : {goat_man,cabbage_man};	--表示状态5的转移关系
			ferrymen=TRUE & cabbage=TRUE & wolf=TRUE&goat=FALSE : {man,cabbage_man};	--状态6的转移关系
			ferrymen=FALSE & cabbage=TRUE & wolf=TRUE&goat=FALSE : {goat_man,man};	--状态7的转移关系
			TRUE: empty;
		esac;

	next(goat):=
		case
			(next(ship)=goat_man)& ferrymen=goat:	next(ferrymen);		--如果运输的是人和羊,那么人和羊都换到另外一边
			 TRUE	: goat;
		esac;
	next(wolf):=
		case
			(next(ship)=wolf_man) & ferrymen=wolf:	next(ferrymen);		--如果运输的是人和狼,那么人和狼都换到另外一边
			TRUE	:wolf;
		esac;
	next(cabbage):=
		case
			(next(ship)=cabbage_man)& ferrymen=cabbage:	next(ferrymen);	--如果运输的人和白菜,那么人和白菜都转移
			TRUE:	cabbage;
		esac;
	next(ferrymen):=	
		case
			(ship=empty): ferrymen;
			TRUE:!ferrymen	;											--每次都需要人的陪同
		esac;

代码的逻辑就是为了反映状态机。
代码设计思路：
ferrymen,goat,wolf,cabbage都是boolean类型的变量，分别表示人、羊、狼、白菜是否在河的右边。当他们的值为FALSE的时候，说明他们在左边，否则在右边。
ship表示每次船上运输的东西，它的取值为goat_man（同时运人和羊）、wolf_man(同时运人和狼)、cabbage_man(同时运人和白菜)、man(只运人)、empty(什么都不运)。
初始化时设置所有的变量的初始值，对应于状态机的初始状态。

写出转移过程：

写出安全过河的条件：

CTLSPEC
	E [(	((goat=wolf)-> (goat=ferrymen)) & ((goat=cabbage)->(goat=ferrymen)))
		U ((cabbage=TRUE)& (goat=TRUE) & (wolf=TRUE) &(ferrymen=TRUE))]

这个条件表示，在羊、白菜、狼、人全部到河右边之前，始终存在当羊和狼在一起时必有人和他们在一起，且当羊和白菜在一起时必然有羊和人在一起。

模型检验

运行上面的代码，得到结果如下：

说明是的确是存在这么一条运输方法的。

输出一条可行的运输路径

因为NuSMV只会举出不符合所需要性质的反例，因此为了得到一条运输路径，可以写出上述的非，表示不存在这么一条路径···，然后NuSMV就会找出一个反例，而这个反例就是我们所需要的运输方法。

检验的性质为：

CTLSPEC
	!E [(	((goat=wolf)-> (goat=ferrymen)) & ((goat=cabbage)->(goat=ferrymen)))
		U ((cabbage=TRUE)& (goat=TRUE) & (wolf=TRUE) &(ferrymen=TRUE))]

模型验证结果：

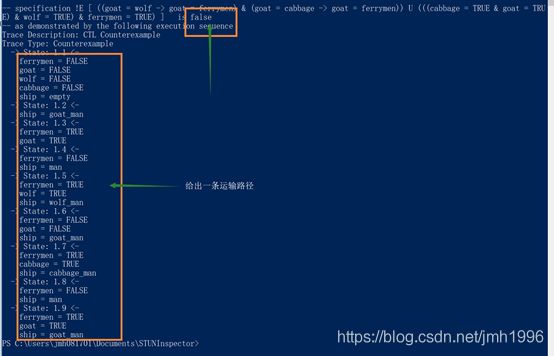
这个结果显示的运输路径如下：
1. 船上先运输羊和人，这样goat=TRUE,ferrymen=TRUE
2. 人在单独过河，这样ferrymen=FALSE
3. 人和狼过河，这样ferrymen=TRUE,goat=TRUE,wolf=TRUE.
4. 人把羊带过河，这样ferrymen=FALSE,goat=FALSE
5. 人把白菜带过河，这样ferrymen=TRUE,cabbage=TRUE
6. 在再单独过河，这样ferrymen=FALSE
7. 最后，人带着羊一起过河。