震惊，全中国有十亿人都不知道它————笛卡尔树（Cartesian_tree）

笛卡尔树

学习笛卡尔树的完整步骤：

1.打开音乐播放器，播放《你是人间四月天》

2.看完这篇博客

 

笛卡尔树：笛卡尔树是带有一些特殊性质的树形结构，好像说了和没有说一样。

性质：笛卡尔树中有这样的二元组（key，value）。

其中key满足二叉搜索树的性质（即父节点的key值大于左儿子，父节点的key值小于右儿子 ）。

value满足堆的性质（即父节点的value值小于子节点的值）。

例如：图片来源维基百科

这里的key是数组位置下标，value是每个位置的值。

可以看出，每个节点的key值都满足二叉搜索树的性质，而value则满足堆的性质。

 

先说说可以用笛卡尔树干什么吧。例如：hdu1506

大致题意就是要求一个最大的矩形面积

 每个块的宽度为1，高度分别是：2 1 4 5 1 3 3。

基本思路：从每个位置开始，向两边分别扩展，如果出现了比自己矮的方块，就停止扩展。如上图所示。求出每个位置可以形成的矩形的面积，再取一个最大值即可。很明显，暴力写肯定是会超时的，所以我们需要用一些小技巧，比如：单调栈，或者我们正在讲的笛卡尔树。

现在用这些值的下标为key，值为value建一颗笛卡尔树。

树建好了，怎么用？？？

对于每一个节点，我们只需要以该节点为根的子树大小size，乘以该节点的value值就好了。比如value值为4的节点，它的子树大小为2，所以该节点往两边扩展出的矩形的面积等于2*4=8。然后就只需要对每个节点都这么求值，最后取个最大值就是本题的答案了。

 

怎么建树？？？

这里我们需要用到“栈”。

1.首先遍历数组，把第一个元素放入栈中。

2.若栈非空，判断栈顶元素的value是否大于当前元素value，是，则出栈，直到栈顶元素不大于当前元素。

2.若栈非空，再把当前元素作为栈顶元素的右儿子。同时把栈顶元素作为当前元素的父亲。

3.把之前出栈的元素作为当前元素的左儿子。把当前元素作为之前出栈元素的父亲。

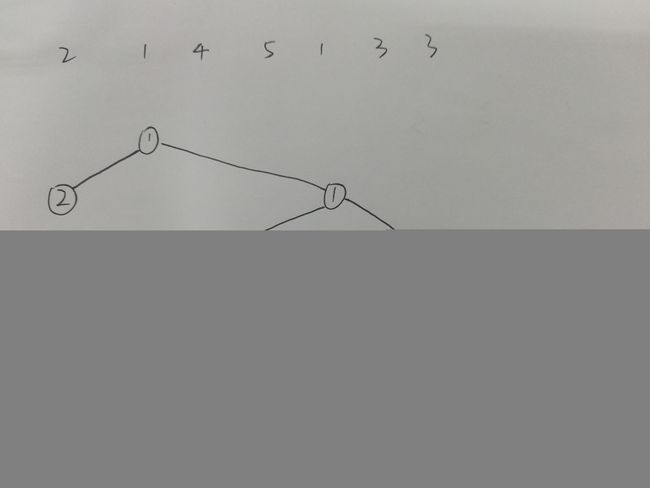
例如：2 1 4 5 1 3 3        （拿上笔和纸，模拟一遍就懂了）

1.先把2入栈，stack（栈中元素）：2。

 

2.当前元素为1，比栈顶元素“2”小，所以2出栈，1入栈。同时2作为1的左儿子，1作为2的父亲。此时stack：1。

 

3.当前元素为4，比栈顶元素“1”大，直接入栈，当前元素作为栈顶元素右儿子，此时stack：1 4。

 

4.当前元素为5，比栈顶元素“4”大，直接入栈，当前元素作为栈顶元素右儿子，此时stack：1 4 5。

 

5.当前元素为1，比栈顶元素“5”小，5出栈，然后再比较，发现比4小，4出栈，再次比较，栈顶元素与当前元素相等。将1入栈，

同时，4做为当前元素的左儿子，当前元素作为4的父亲，当前元素作为栈顶元素的右儿子，栈顶元素作为当前元素的父亲。

此时stack：1 1。

6.当前元素为3，比栈顶元素大，直接入栈，当前元素作为栈顶元素右儿子。此时stack：1 1 3。

7.当前元素为3，比栈顶元素大，直接入栈，当前元素作为栈顶元素右儿子。此时stack：1 1 3 3。

 

如果觉得有帮助，就给我点赞吧!!!!!!!!! (@.@)

点赞！！！！

点赞啊！！！！(#.#)

最后，代码：

#include
using namespace std;
const int maxn=1e5+100;
int arr[maxn];
long long int ans;
struct node
{
    int parent;
    int l,r;
    int val;
}tree[maxn];
int build_cartesian_tree(int n)
{
    int k=-1;
    int top=-1;
    int stk[maxn];
    for(int i=1;i<=n;++i)
    {
        tree[i].val=arr[i];
        while(k>=0&&arr[stk[k]]>arr[i])
            --k;
        if(k>=0)
        {
            tree[stk[k]].r=i;
            tree[i].parent=stk[k];
        }
        if(k!=top)
        {
            tree[i].l=stk[k+1];
            tree[stk[k+1]].parent=i;
        }
        stk[++k]=i;
        top=k;
    }
    tree[stk[0]].parent=-1;
    return stk[0];
}
int dfs(int u)
{
    if(!u)
        return 0;
    int sz=1;
    sz+=dfs(tree[u].l);
    sz+=dfs(tree[u].r);
    ans=max(ans,(long long int )sz*tree[u].val);
    return sz;
}