【矩阵乘法】【倍增】美食家（luogu 6772）

美食家

题目大意

给你一个有向图，边权为经过所需时间
每个点有一个点权，有些点还有有特殊的点权
当你到达一个点后，可以获得该点的点权（重复经过可以重复获得，但不能停留），若在某个时间到某个点，则可获得该特殊点权
现在问你从点1出发走，在时间T回到1得到的最大点权和是多少

输入样例#1

3 4 11 0
1 3 4
1 2 1
2 1 3
2 3 2
3 1 4

输出样例#1

13

输入样例#2

4 8 16 3
3 1 2 4
1 2 1
1 3 1
1 3 2
3 4 3
2 3 2
3 2 1
4 2 1
4 1 5
3 3 5
1 2 5
5 4 20

输出样例#2

39

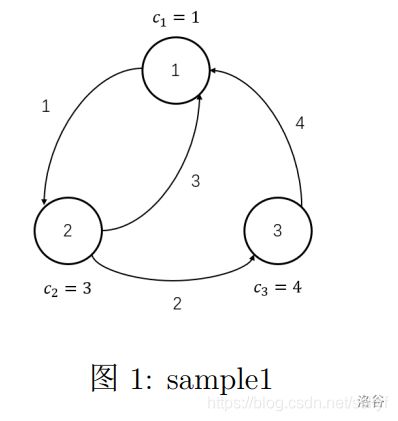
样例解释#1

对于上图，小 W 一种为期 11 天的可行旅游方案为 $1\to 2\to 1\to 2\to 3\to 1$

第 0 天，小 $W$ 从城市 1 开始旅行，获得愉悦值 1 并向城市 2 出发。
第 1 天，小 $W$ 到达城市 2，获得愉悦值 3 并向城市 1 出发。
第 4 天，小 $W$ 到达城市 1，获得愉悦值 1 并向城市 2 出发。
第 5 天，小 $W$ 到达城市 2，获得愉悦值 3 并向城市 3 出发。
第 7 天，小 $W$ 到达城市 3，获得愉悦值 4 并向城市 1 出发。
第 11 天，小 $W$ 到达城市 1，获得愉悦值 1 并结束旅行。
小 W 在该旅行中获得的愉悦值之和为 13。

样例解释#2

最优方案为 $1\to 3\to 4\to 2\to 3\to 4\to 1$

第 0 天，小 $W$ 从城市 1 开始旅行，获得愉悦值 3 并沿道路 3 通行。
第 2 天，小 $W$ 到达城市 3，获得愉悦值 2 并沿道路 4 通行。
第 5 天，小 $W$ 到达城市 4，由于美食节获得愉悦值 20+4 并沿道路 7 通行。
第 6 天，小 $W$ 到达城市 2，获得愉悦值 1 并沿道路 5 通行。
第 8 天，小 $W$ 到达城市 3，获得愉悦值 2 并沿道路 4 通行。
第 11 天，小 $W$ 到达城市 4，获得愉悦值 4 并沿道路 8 通行。
第 16 天，小 $W$ 到达城市 1，获得愉悦值 3 并结束旅行。
小 W 获得的愉悦值之和为 39。

数据范围

$1\le n\le 50，n\le m\le 501，0\le k\le 200，1\le t_i\le T\le 10^9。$
$1\le w_i\le 5，1\le c_i\le 52501，1\le u_i,v_i,x_i\le n，1\le y_i\le 10^9$

解题思路

我们发现$w$很小,我们可以把一条边分成若干长度为1的边，这样点最多只有250个
当没有特殊点权时
我们可以用邻接矩阵跑矩阵乘法
时间$O((nw{)}^{3}logT)$
如果有特殊点权时直接暴力跑矩阵乘法那时间是$O((nw{)}^{3}klogT)$
会TLE
我们与处理出$f_i=A^{2^i}$
然后倍增求特殊点权到特殊点权之间的时间,然后加上相应的权值
向量乘矩阵时间$O((nw{)}^2)$
总时间$O((nw{)}^{3}logT+(nw{)}^{2}klogT)$

代码

#include
#include
#include
#include
#define ll long long
#define p(x, y) ((x * 5) + (y))
using namespace std;
ll n, m, t, k, x, y, z, w, nn, now, pw[35], a[260], b[260];
struct matrix
{
	ll a[260][260];
}f[35];
struct node
{
	ll t, v, s;
}q[210];
bool cmp(node a, node b)
{
	return a.t < b.t;
}
matrix jc(matrix &a)
{
	matrix b;
	memset(b.a, 0xcf, sizeof(b.a));
	for (ll i = 0; i < nn; ++i)
		for (ll j = 0; j < nn; ++j)
			for (ll k = 0; k < nn; ++k)
				b.a[i][j] = max(b.a[i][j], a.a[i][k] + a.a[k][j]);//矩阵乘矩阵
	return b;
}
void js(matrix &b)
{
	ll c[260];
	memcpy(c, a, sizeof(a));
	memset(a, 0xcf, sizeof(a));
	for (ll i = 0; i < nn; ++i)
		for (ll j = 0; j < nn; ++j)
			a[j] = max(a[j], c[i] + b.a[i][j]);//向量乘矩阵
	return;
}
void power(ll x)
{
	for (ll i = 0; i <= w; ++i)
		if (x&pw[i]) js(f[i]);
	return;
}
int main()
{
	scanf("%lld%lld%lld%lld", &n, &m, &t, &k);
	nn = n * 5;
	memset(f[0].a, 0xcf, sizeof(f[0].a));
	for (ll i = 0; i < n; ++i)
	{
		scanf("%lld", &b[i]);
		for (ll j = 1; j < 5; ++j)
			f[0].a[p(i, j)][p(i, j - 1)] = 0;//拆分点
	}
	for (ll i = 1; i <= m; ++i)
	{
		scanf("%lld%lld%lld", &x, &y, &z);
		x--;
		y--;
		f[0].a[p(x, 0)][p(y, z - 1)] = b[y];//连边
	}
	pw[0] = 1;
	while(pw[w] * 2 <= t)
	{
		w++;
		pw[w] = pw[w - 1] * 2;
		f[w] = jc(f[w - 1]);//计算f
	}
	for (ll i = 1; i <= k; ++i)
		scanf("%lld%lld%lld", &q[i].t, &q[i].v, &q[i].s), q[i].v--;
	sort(q + 1, q + 1 + k, cmp);
	q[++k] = (node){t, 0, 0};
	memset(a, 0xcf, sizeof(a));
	a[0] = b[0];
	for (ll i = 1; i <= k; ++i)
	{
		power(q[i].t - now);//倍增
		a[p(q[i].v, 0)] += q[i].s;
		now = q[i].t;
	}
	if (a[0] < 0) printf("-1");
	else printf("%lld", a[0]);
	return 0;
}