取石子游戏
1 取石子游戏
1.1 描述
有两堆石子,数量任意,可以不同。游戏开始由两个人轮流取石子。游戏规定,每次有两种不同的取法,一是可以在任意的一堆中取走任意多的石子;二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。
现在给出初始的两堆石子的数目a和b,如果轮到你先取,假设双方都采取最好的策略,问最后你是胜者还是败者。如果你是胜者,输出Win,否则输出Lose。
例如,a=3,b=1, 则输出Win(你先在a中取一个,此时a=2,b=1,此时无论对方怎么取,你都能将所有石子都拿走)。
1.2 思路
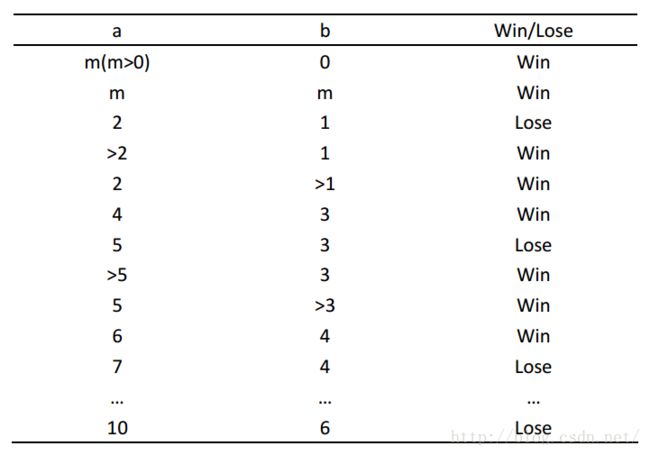
首先,我从0开始枚举所有可能的情况,发现:其中,所有Loose的情况为(2,1),(5,3),(7,4),(6,10)...,用图形表示为:
因为:
2 - 1 = 1
5 - 3 = 2
7 - 4 = 3
10 - 6 = 4
于是猜测所有Lose的情况为a - b = k(设a > b),k从1一直递增,a,b取值不重复,从1开始。
1.3 代码
代码思路是,构造一个包含所有Lose情况的数组p,数组中所有Lose的数对值相同。比如,(i,j)为一个Lose对,那么p[i]等于p[j],这样给定a,b时,判断p[a]和p[b]是否相等,如果相等,那么其Lose。
from __future__ import print_function
def get_failed_pairs(a, b):
c = a if a > b else b
pairs = [0] * (c+1)
k = 1
for i in range(1, c + 1):
if i + k <= c and not pairs[i]:
pairs[i] = pairs[i+k] = i
k += 1
return pairs
def take_the_stone(a, b, pairs):
if a != b and (pairs[a] == pairs[b] != 0):
return False
return True
pairs = get_failed_pairs(a, b)
print(take_the_stone(a, b, pairs) and 'Win' or 'Lose')
1.4 后续
另,在结题报告中看到一种规律叫做‘奇异态势’,有两个特点:
1. 无法从一个奇异态势一步走到另一个奇异态势;
2. 任何非奇异态势可以一步走到某一个奇异态势。
可构建以下奇异态势,前几组分别为(0,0),(1,2),(3,5),(4,7),(6,10),(8,13)....满足:
1)各奇异态势间无重复元素;
2)步长(|a-b|)递增,保证各不相同