DP - 状压DP - Corn Fields(POJ - 3254) + 炮兵阵地(NOI - 2001)

DP - 状压DP - Corn Fields(POJ - 3254) + 炮兵阵地(NOI - 2001)

1、Corn Fields(POJ - 3254)

农夫约翰的土地由M*N个小方格组成，现在他要在土地里种植玉米。

非常遗憾，部分土地是不育的，无法种植。

而且，相邻的土地不能同时种植玉米，也就是说种植玉米的所有方格之间都不会有公共边缘。

现在给定土地的大小，请你求出共有多少种种植方法。

土地上什么都不种也算一种方法。

输入格式
第1行包含两个整数M和N。

第2…M+1行：每行包含N个整数0或1，用来描述整个土地的状况，1表示该块土地肥沃，0表示该块土地不育。

输出格式
输出总种植方法对100000000取模后的值。

数据范围
1≤M,N≤12

输入样例：
2 3
1 1 1
0 1 0
输出样例：
9

---

分析：

$与——$《SGU - 223 - Little Kings》$类似，是经典的棋盘氏状压DP。$

$在一个n\times m的方格上放物品，每件物品将额外占据上下左右四个位置，要求方案总数。$

$状态表示，f[i][j]:已经放好前i行，且第i行的状态为j方案总数。$

$$\begin{gathered} 状态计算： \\ 由于第i行摆放的状态仅与i-1行有关，设第i行的二进制状态是a，第i-1行的二进制状态是b， \\ 若二进制的某位是1，表示对应的位置放物品，否则表示不放物品。 \\ 需要保证相邻两行同一列不能同时放物品，即a\&b=0。 \end{gathered}$$

$$\begin{gathered} 只要满足a\&b=0，第i行的状态就能由第i-1行转移而来，即f[i][a]+=f[i-1][b]。 \\ 前提是状态都是合法的，即同一行的相邻位置也不能摆放物品，即a与b的二进制表示中不能有连续的1。 \end{gathered}$$

$$\begin{gathered} 本题还有一个限制，部分位置不能摆放物品， \\ 通过将每一行输入的数以二进制的形式单独存入数组g， \\ 若元素为0，表示当前位置不可放物品，我们将对应位存1，反之，对应位存0， \\ 这样，若第i行状态g[i]\&a\ne 0，则说明当前状态有物品放到了禁止摆放的位置上。 \end{gathered}$$

具体落实：

$①、首先处理数组g，将每一行的状态表示成一个二进制数。$

$②、预处理所有合法的状态，即不能在相邻的位置摆放物品，反应到二进制状态上就是不能有相邻的1。$

$③、能够相互转移的状态之间用head数组来映射。$

代码：

#include
#include
#include

using namespace std;

const int N=15,M=1<<12,mod=1e8;

int n,m,g[N],f[N][M];
vector<int> state;
vector<int> head[M];

bool check(int x)
{
    for(int i=0;i<m-1;i++)
        if((x>>i)&1 && (x>>i+1)&1)
            return false;
    return true;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=0;j<m;j++)
        {
            int t;
            cin>>t;
            g[i]+= !t << j;
        }
            
    for(int i=0;i<1<<m;i++)
        if(check(i))
            state.push_back(i);
        
    int len=state.size();
    for(int i=0;i<len;i++)
        for(int j=0;j<len;j++)
        {
            int a=state[i],b=state[j];
            if((a&b)==0) head[i].push_back(j);
        }
        
    f[0][0]=1;
    for(int i=1;i<=n+1;i++)
        for(int a=0;a<len;a++)
            for(int b:head[a])
            {
                if(g[i]&state[a]) continue;
                f[i][state[a]]=(f[i][state[a]]+f[i-1][state[b]])%mod;
            }
            
    cout<<f[n+1][0]<<endl;
    
    return 0;
}

---

2、炮兵阵地(NOI - 2001)

司令部的将军们打算在NM的网格地图上部署他们的炮兵部队。一个NM的地图由N行M列组成，地图的每一格可能是山地（用”H” 表示），也可能是平原（用”P”表示），如下图。

在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

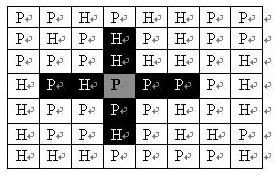
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。

图上其它白色网格均攻击不到。

从图上可见炮兵的攻击范围不受地形的影响。

现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式
第一行包含两个由空格分割开的正整数，分别表示N和M；

接下来的N行，每一行含有连续的M个字符(‘P’或者’H’)，中间没有空格。按顺序表示地图中每一行的数据。

输出格式
仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

数据范围
N≤100,M≤10

输入样例：
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
输出样例：
6

---

分析：

$$\begin{gathered} 本题是上一题的一个简单扩展。 \\ 上一题摆放的物品额外占据上下左右四个位置，本题将在上一题物品的基础上再另外向四个方向延伸一位。 \end{gathered}$$

$即每个物品将额外占据上下左右四个方向上各两个位置的空间。$

$要求最多能摆放的物品数量。$

$由于第i行的摆放状态不仅与第i-1行的状态有关，还有第i-2的状态有关，因此本题的状态表示需要三维。$

$状态表示，f[i][j][k]:已经摆放了前i行，且第i-1行的状态是j，第i行的状态是k，最多摆放的物品数量。$

$$\begin{gathered} 状态计算： \\ 假设第i行的状态是b，第i-1行的状态是a，第i+1行的状态是c， \\ 首先要保证所有的状态都是合法的，即不能存在摆放间隔小于2的物品。 \\ ①、每一列：不能同时存在摆放间隔小于2的的物品，需满足a\&b=0且a\&c=0且b\&c=0。 \end{gathered}$$
$②、每一行：物品不能摆放在禁止摆放的位置，需满足g[i]\&b=0且g[i-1]\&a=0。$

$$\begin{gathered} 满足以上两个条件，状态i即可有状态i-1转移而来，即f[i][a][b]+=f[i-1][c][a]+cnt[b]， \\ 其中cnt[b]是第i行摆放的物品个数，对应到二进制上就是b中1的个数。 \end{gathered}$$

$$\begin{gathered} 另外，由于本题空间限制较严格，可以采用滚动数组的方式优化空间。 \\ 具体方式就说在第一维求取的过程中，将第一维的下标\&1。 \end{gathered}$$

注意：

$$\begin{gathered} 本题在枚举合法方案时，移位次数上限是m-1，不是m-2， \\ 因为只要相邻一位或者两位有一个1，就是不合法的。 \end{gathered}$$

代码：

#include
#include
#include

using namespace std;

const int N=110,M=1<<10;

int n,m,g[N],f[2][M][M],cnt[M];
vector<int> state;

bool check(int x)
{
    for(int i=0;i<m-1;i++)
        if( (x>>i)&1 && ((x>>i+1)&1 || (x>>i+2)&1) ) 
            return false;
    return true;
}

int Count(int x)
{
    int res=0;
    for(int i=0;i<m;i++) res+=(x>>i)&1;
    return res;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=0;j<m;j++)
        {
            char c;
            cin>>c;
            if(c=='H') g[i]+= 1<<j;
        }
        
    for(int i=0;i<1<<m;i++)
        if(check(i))
        {
            state.push_back(i);
            cnt[i]=Count(i);
        }
        
    int len=state.size();
    for(int i=1;i<=n+2;i++)
        for(int j=0;j<len;j++)
            for(int k=0;k<len;k++)
                for(int u=0;u<len;u++)
                {
                    int a=state[j],b=state[k],c=state[u];
                    if((a&b) | (b&c) | (a&c)) continue;
                    if((g[i]&b) | (g[i-1]&a)) continue;
                    f[i&1][a][b]=max(f[i&1][a][b],f[i-1 & 1][c][a]+cnt[b]);
                }
                
    cout<<f[n+2 & 1][0][0]<<endl;
    
    return 0;
}