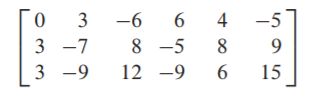yilyil
yilyil

矩阵解线性方程

学习自《linear algebra and its application》

二元线型方程

矩阵解线性方程_第1张图片
矩阵解线性方程_第2张图片
我们熟知的两个未知数两个方程组的解，等价于两条直线的交点
可能交于一点（一个解），平行（无解），重合（两条直线上每个点交点）
有交点相容，无交点不相容

用矩阵表示方程组

我们使用矩阵来包含一个方程组的主要信息
矩阵解线性方程_第3张图片
上面一个是系数矩阵，一个是曾广矩阵

那么如何求解，首先我们看看先后关系
矩阵解线性方程_第4张图片
答案很明显了，解方程也就是对矩阵的变换

我们来看组无解的情况：
矩阵解线性方程_第5张图片
当化成第一个三角形时 0 = 5 2 0=\frac {5}{2} 0=25​ 显然不成立

解任意线型方程组

下面是带来解任意线型方程组的行化简算法

阶梯型

  1. 每一非零行在每一零行之上
  2. 每一行的先导元素所在列位于前一行先导元素的釉面
  3. 某一先导元素所在的列下方元素都是0
    矩阵解线性方程_第6张图片

简化阶梯型

  1. 以上三点
  2. 每一非0行的先导元素是1
  3. 每一先导元素1是该元素所在列的唯一非0元素
    矩阵解线性方程_第7张图片

例子：简化下面的增广矩阵
在这里插入图片描述

在这里插入图片描述
由最左边的非零列开始，作为第一个主元列，然后选取一个非零元素作为主元，若有必要的话，兑换两行
用倍加行变换将主元下面的元素变为0
在这里插入图片描述
从第二行开始由最左边的非零列开始，选取新主元行的主元，然后用倍加行变换将主元下面的元素变为0
在这里插入图片描述
选取第三行的，直接就成立了，到此为止，阶梯型有了，如果需要简化阶梯型，还需要下述步骤

在这里插入图片描述

首先我们将最三行的，所在列其他的变为0（本身为1，所以不需要缩小）

在这里插入图片描述
然后我们处理第二行的，这是需要缩小和所在列其他的变为0

在这里插入图片描述
然后我们处理第一行的，这是只需要缩小，到此为止，最简阶梯型好了
最后我们得到的是线型方程组的一种显示表示法，如下面我们已经化成简化阶梯型
矩阵解线性方程_第8张图片
x 1 x_1 x1​和 x 2 x_2 x2​ 为基本变量， x 3 x_3 x3​ 为自由变量，然后我们用自由变量表示基本变量即可，最后式子给出了通解。

如何区分基本变量：则非零行的首非零元所在列对应的就是约束变量,其余变量即为自由变量

你可能感兴趣的:(矩阵解线性方程)

  • 今日联对0306 诗图佳得
    自对联：烟销皓月临江浒，水漫金山荡塔裙。一一肖士平2020.3.6.1、试对肖老师联：烟销皓月临江浒，夜笼寒沙梦晚舟。耀哥求正2、试对萧老师联:烟销浩月临江浒，雾散乾坤解汉城。秀霞习作请各位老师校正3、自对联：烟销皓月临江浒，水漫金山荡塔裙。一一肖士平2020.3.6.4、试对肖老师垫场联：烟销皓月临江浒，雾锁寒林缈葉丛。小智求正[抱拳]5、试对肖老师联：烟销皓月临江浒；风卷乱云入峰巅。一一五品6
  • linux 发展史 种树的猴子 内核java操作系统linux大数据
    linux发展史说明此前对linux认识模糊一知半解，近期通过学习将自己对于linux的发展总结一下方便大家日后的学习。那Linux是目前一款非常火热的开源操作系统，可是linux是什么时候出现的，又是因为什么样的原因被开发出来的呢。以下将对linux的发展历程进行详细的讲解。目录一、Linux发展背景二、UINIX的诞生三、UNIX的重要分支-BSD的诞生四、Minix的诞生五、GNU与Free
  • 推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
    importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
  • 《吹牛大王历险记》读书随笔 赵炳森
    这本书的作者是埃·拉斯伯戈·毕尔格。（没查到相关内容，好像他只写过《吹牛大王历险记》。）最让人百思不得其解的是他居然能自己拉自己的辫子出泥潭？！我觉得自己拉自己的辫子只会把自己的辫子拉断，而不会飞出泥潭。（问:图片中底下的屁股为什么插了一根钢针？）屁股底下居然有根钢针？在泥潭应该是滑滑的吧，可是他怎么能夹紧马肚呢？马肚子应该是在马的下方。还有如果能从泥潭里把连人带马都给拽出来的话，他力气肯定很大，
  • Python算法L5：贪心算法 小熊同学哦 Python算法算法python贪心算法
    Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点：缺点：结语贪心算法（GreedyAlgorithm）是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是，在保证每一步局部最优的情况下，希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
  • matlab delsat = setdiff(1:69,unique(Eph(30,:)))； 语句含义 黄卷青灯77 matlab开发语言setdiff
    这行MATLAB代码用于计算在范围1:69中不包含在Eph矩阵第30行的唯一值集合中的所有元素。具体解释如下：delsat=setdiff(1:69,unique(Eph(30,:)));解释Eph(30,:)Eph(30,:)提取矩阵Eph的第30行的所有列元素。这是一个行向量，包含了第30行的所有值。unique(Eph(30,:))unique函数返回Eph(30,:)中的唯一元素。这意味着
  • 第二十五辑-安尘乱物 wallowed
    1、《劳犁》作犁耕土解炎林，劳碌秋丰四两金。挥汗佝偻衣褴褛，卖得如洗衬寒贫。春种南山锄造力，傍老倚仗体民心。颗籽无收黍稷尘，农田饥劬苦疫病。牛羊冷炙食蚕桑，丁壮耒耜宿闲勤。归来未已开红豆，篱落花稀麦苗青。米贵征徭生柴火，荒草凄清渐鸡鸣。谷雨时节方期许，择日又是复曾经。2、《忘言》久别似相识，对酒客长安。嘘唏一仗夜，临行却忘言。江雪空投岸，梨花淡云烟。若问有缘人，相窥两不厌。莫作酒魂归，窗台结生寒。
  • 2022-06-29 感恩学习相信小陶
    感恩！六点签到相信很多人都有过这样的经验，拼命想的时候答案怎么都想不出来，不去想的时候，答案却自动冒出来了。为什么？这是因为潜意识也会工作，它非常神奇。你要相信，那些百思不得其解的问题早已扎根在你的头脑中，即使你不再刻意去想，潜意识也会自动围着它转。或许有一天，你会突然得到答案。这也是为什么有时我们会有顿悟的感觉。学会等待，也是进行持续思考的一个重要方法。
  • 今夜的雨欠费了？ 洛小简
    文/洛小简这里是醉人的宜宾，这是枫叶的十月。是不是得罪了龙王爷，让这雨肆无忌惮，却也毫无章法。那雨声暴躁，或早晨，或是午后，更多的在夜里。可今夜它睡着了，我看怕是欠费了，还未充值。但偏偏我醒了，醒在以往下雨的凌晨。耳边还有车声，最恨那乌鸦，又在远处偷鸣。就让龙王息怒吧，雨神也要歇一歇，持久的战斗体力无存，怎么给冬天一个雪的交待？那我的梦里还会不会下雪，是否如我所愿，这又是未解的谜题。幸好这雨也会欠
  • 好运来 是露漫漫呀
    4月9日下午17.45分晴此时学校里广播站放着激情热烈的歌曲——《好运来》。“好运来，祝你好运来……”第一瞬间，我想到了他们是放这首歌是为补考的同学招来好运气的。然后我思绪飞扬，飘到了高中考试前同学放这首歌来抚平心态。飘到了高考前整理班级课桌时，学校喇叭里大大咧咧放着《好运来》……疲惫的我会心一笑。飘到了上学期考细解实验试卷时的那个中午青春小胖放这首歌来招好运，祈祷考的都会…………关于《好运来》的
  • 高级UI<第二十四篇>：Android中用到的矩阵常识 NoBugException
    （1）定义在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。由m×n个数aij排成的m行n列的数表称为m行n列的矩阵，简称m×n矩阵。记作：图片.png这m×n个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数aij为(i,j)元的矩阵可记为(aij)或(aij)m×n，m×n矩阵A也记作Amn。元素是实数的矩阵称为实矩阵，元素是复
  • 滑动窗口+动态规划 wniuniu_ 算法动态规划算法
    前言：分析这个题目的时候，就知道要这两个线段要分开，但是要保证得到最优解，那么我们在选取第二根线段的时候，要保证我们第一根线段是左边最优解并且我们选的两根线段的右端点一定是我们的数组的点（贪心思想）classSolution{public:intmaximizeWin(vector&prizePositions,intk){intn=prizePositions.size();vectormx(n
  • 【鸿蒙应用】总结一下ArkUI 读心悦 鸿蒙基础鸿蒙应用
    ArkUI是HarmonyOS应用界面的UI开发框架，提供了简洁的UI语法、UI组件、动画机制和事件交互等等UI开发基础，以此满足应用开发者对UI界面开发的需求。组件是界面搭建的最小单位，开发者通过多种组件的组合构成完整的界面。页面是ArkUI最小的调度分隔单位，开发者可以将应用设计为多个功能页面，每一个页面进行单独的文件管理，并且通过页面路由API完成页面之间的调度管理，以此来实现应用内功能的解
  • 【机器人建模和控制】读书笔记 Piccab0o 机器人
    机器人建模和控制——马克·斯庞A.x10=x1∙x0x^0_1=x_1\bulletx_0x10=x1∙x0，其实就是：1）x1x_1x1轴向量在O0O_0O0系下的坐标2）在x0x_0x0轴上的投影3）坐标变换矩阵的R10R_1^0R10的第一个元素B.点p在o1x1y1z1o_1x_1y_1z_1o1x1y1z1系下的坐标p1p^1p1可以表示为：p=ux1+vy1+wz1p=ux_1+vy_
  • python 读写csv文件方法 菩提本无树007 pythonpandas开发语言
    csv是一种结构化文件，可以将文本转化成矩阵的形式，方便程序读取和处理。下面来介绍一下使用python读写csv文件的方法：1.首先需要使用pip安装python包，然后将csv文件解压到一个文件夹下2.使用pip安装python包，安装完成后在终端输入：3.在终端输入命令：4.输入完成后，打开终端，在命令行输入以下代码：5.最后输出结果，可以看到csv文件已经打开了。6.将csv文件放入到pyt
  • MATLAB语言基础教程、 小项目1：简单的计算器、 小项目2：有页面的计算器、使用App Designer创建GUI计算器 azuredragonz 学习教程matlab开发语言
    MATLABMATLAB语言基础教程1.MATLAB简介2.基本语法变量与赋值向量与矩阵矩阵运算数学函数控制流3.函数4.绘图案例：简单方程求解小项目1：简单的科学计算器功能代码项目说明小项目2：有页面的计算器使用AppDesigner创建GUI计算器主要步骤：完整代码（使用MATLAB编写）说明：如何运行：小项目总结MATLAB语言基础教程1.MATLAB简介MATLAB（矩阵实验室）是一种用于
  • 今天到底是谁的生日 马蹄踏碎落叶
    在我的记忆中，最使我百思不得其解的就是奶奶的六十大寿，那天发生的事。早晨九点多，我们全家已经把家里打扫的一尘不染，为祝贺奶奶60大寿的东西也准备齐全了，一会儿小姑，大姑全来了！他们各自带了礼物。该准备午餐了，奶奶让我去拿围裙，一走进房间看见一地的瓜子壳，像下了雪似的积了厚厚一层。走进客厅姑父和大爷正在打牌，笑声此起彼伏，而老寿星奶奶呢却正在厨房烧菜，忙得像一只陀螺。大爷说:“我快渴死了，奶奶匆匆忙
  • Fork/Join框架与ForkJoinPool 浪白条
    1.Fork/Join框架fork操作的作用是把一个大的问题划分成若干个较小的问题。在这个划分过程一般是递归进行的。直到可以直接进行计算。需要恰当地选取子问题的大小。太大的子问题不利于通过并行方式来提高性能，而太小的子问题则会带来较大的额外开销。每个子问题计算完成后，可以得到关于整个问题的部分解。join操作的作用是把这些分解手机组织起来，得到完整解。简单的说，ForkJoin其核心思想就是分治。
  • np.identity()/np.eye() 听风1996
    两个函数的原型为：np.identity(n,dtype=None)np.eye(N,M=None,k=0,dtype=)；np.identity只能创建方形矩阵np.eye可以创建矩形矩阵，且k值可以调节，为1的对角线的位置偏离度，0居中，1向上偏离1，2偏离2，以此类推，-1向下偏离。值绝对值过大就偏离出去了，整个矩阵就全是0了。两者在创建单位矩阵上，并无区别，两者的区别主要在接口上；np.i
  • 2022-04-04 N4一念
    佛家讲世间出世间打成一片，世间即出世间，只是重点在出世间，但也不能离开世间而出世间。道家也是如此，虽然这种词语并不多。老子说:“控其锐，解其纷，和其光，同其尘'。这四句句法相同，但并不好讲。“其”指道，即道心。分解地讲道心当然代表光明，但将光明孤悬，或在深山中修道，这境界也并不很高。“和其光”的意思是把光明浑化柔和一下，就是要人勿露锋芒。“挫其锐”也是勿露锋利的意思。因此，人喜言“韬光养晦”，要人
  • 图像匹配---（Python） 阳光下的Smiles Python图像处理
    图像匹配---（Python）图像匹配分为以灰度为基础的匹配和以特征为基础的匹配：（1）灰度匹配是基于像素的匹配。灰度匹配通过利用某种相似性度量，如相关函数、协方差函数、差平方和、差绝对值和等测度极值，判定两幅图像中的对应关系。（2）特征匹配则是基于区域的匹配。基于特征的匹配所处理的图像一般包含的特征有颜色特征、纹理特征、形状特征、空间位置特征等1、差分矩阵求和差分矩阵=图像A矩阵数据-图像B矩阵
  • 洛谷P1719 最大加权矩形 0hang 算法c++开发语言
    洛谷P1719最大加权矩形题目描述为了更好的备战NOIP2013，电脑组的几个女孩子LYQ,ZSC,ZHQ认为，我们不光需要机房，我们还需要运动，于是就决定找校长申请一块电脑组的课余运动场地，听说她们都是电脑组的高手，校长没有马上答应他们，而是先给她们出了一道数学题，并且告诉她们：你们能获得的运动场地的面积就是你们能找到的这个最大的数字。校长先给他们一个n\timesnn×n矩阵。要求矩阵中最大加
  • 4×4矩阵键盘详解（STM32） 辰哥单片机设计 STM32传感器教学矩阵计算机外设stm32嵌入式硬件单片机传感器
    目录一、介绍二、传感器原理1.原理图2.工作原理介绍三、程序设计main.c文件button4_4.h文件button4_4.c文件四、实验效果五、资料获取项目分享一、介绍矩阵键盘，又称为行列式键盘，是用4条I/O线作为行线，4条I/O线作为列线组成的键盘。在行线和列线的每一个交叉点上设置一个按键，因此键盘中按键的个数是4×4个。这种行列式键盘结构能够有效地提高单片机系统中I/O口的利用率，节约单
  • 【 日本鲫鱼钓 】浮游矶钓不同目标鱼不同钓法，日本专业矶钓书籍 夏说钓鱼
    夏说钓鱼，聊海外钓鱼，助钓友钓技！浮游矶钓不同目标鱼不同钓法，翻译来自《日本図解釣り入門基礎から始める海のウキ釣り入門》说到浮钓，由于它的目标鱼类多种多样，因此针对不同类型的目标也会有不同的浮钓方式。下面介绍一下同种类的浮钓方法和目标鱼类。【伸缩竿的小型钓法】用4.5～5.3米的伸缩竿的钓鱼方法。与矶钓竿相比，这种钓鱼竿更加轻便，连儿童也可以使用。目标鱼类有鲰虎鱼、海鲫、沙氏下鱲、竹荚鱼、鲪鱼、小
  • STM32——看门狗通俗解析 百里与司空 stm32嵌入式硬件单片机门控循环单元
    笔者在学习看门狗的视频后，对看门狗仍然是一知半解，后面在实际应用中发现它是一个很好用的检测或者调试工具。所以总结一下笔者作为初学小白对看门狗的理解。主函数初始化阶段、循环阶段和复位众所周知，程序的运行一般是这样的：程序在进入循环阶段之前，会在初始化阶段将每个寄存器或者某些变量赋值。初始化阶段的代码执行一次后，就不再执行了。而循环阶段的代码会执行很多次，一直循环反复的执行下去。这时，如果进行了复位，
  • 抖音开始怎么吸粉（可以试试这几种办法） 配音新手圈
    如何在抖音短视频平台上快速积累人气和粉丝，抖音短视频平台已成为“我们媒体”和全媒体矩阵，是客户获取、推广和收入的重要平台之一。兼职副业推荐公众号，配音新手圈，声优配音圈，新配音兼职圈，配音就业圈，鼎音副业，有声新手圈，每天更新各种远程工作与在线兼职，职位包括：写手、程序开发、剪辑、设计、翻译、配音、无门槛、插画、翻译、等等。。。每日更新兼职。但对于初学者来说，如何在抖音上建立自己的品牌，积累粉丝，
  • Linux常用文件压缩/解压命令格式大全（tar、gzip、bzip2、zip、compress、cpio、compress、dd）建议收藏 狱典司 Linux网络服务linux操作系统shell
    Linux常用文件压缩/解压命令格式大全1.tar2.gzip3.bzip24.zip5.compress6.cpio7.dd1.tar打包备份后的文件包缀：.tar作用：用来对系统上的文件作备份与恢复，可以将系统上多个文件组构成一个tar文件备份到磁盘内或写入到一般的文件（文件名为*.tar）上，也可以将文件从一个tar文件解回到原来的系统中。说明：仅能将一个目录下的所有文件变成一个文件，不具备
  • 云服务业界动态简报-20180128 Captain7
    一、青云青云QingCloud推出深度学习平台DeepLearningonQingCloud，包含了主流的深度学习框架及数据科学工具包，通过QingCloudAppCenter一键部署交付，可以让算法工程师和数据科学家快速构建深度学习开发环境，将更多的精力放在模型和算法调优。二、腾讯云1.腾讯云正式发布腾讯专有云TCE(TencentCloudEnterprise)矩阵，涵盖企业版、大数据版、AI
  • OpenGL之基础纹理一 我的大好时光
    先看下效果图：纹理效果图.pngDemo下载地址：点击下载一、像素图像的数据包装图像存储空间=图像width*图像height*每个像素的字节数ps：有一张RGB的图像（每个颜色通道8位），图像的宽度199个像素，每行需要存储多少空间？解：8位为一个字节，有三个颜色，所以一个RGB需要3个字节存储。199（width）*1（height）*3(字节)二、像素的存储方式/**@parampname:
  • 麻黄汤续讲与大小青龙汤 c1af95f51459
    麻黄九禁脉浮紧者，法当汗出而解，若身重心悸者，不可发汗，须自汗出乃愈。所以然者，尺中脉微此里虚也，须里实，津液自和，便自汗出愈。脉浮紧的人照理说要发汗，可是如果身体重心悸的话，就不可以发汗。其实这个发汗不一定是麻黄汤，大青龙汤也会发汗。但是单独身体重的话不能够成不发汗的理由。因为感冒，很多人身体都是重重的，但是身重，心悸，就不可以发汗，因为心悸往往是阳虚。如果尺脉跳的很慢的人也不可以发汗，尺脉代表
  • knob UI插件使用 换个号韩国红果果 JavaScriptjsonpknob
    图形是用canvas绘制的 js代码 var paras = { max:800, min:100, skin:'tron',//button type thickness:.3,//button width width:'200',//define canvas width.,canvas height displayInput:'tr
  • Android+Jquery Mobile学习系列(5)-SQLite数据库 白糖_ JQuery Mobile
    目录导航   SQLite是轻量级的、嵌入式的、关系型数据库，目前已经在iPhone、Android等手机系统中使用,SQLite可移植性好，很容易使用，很小，高效而且可靠。   因为Android已经集成了SQLite，所以开发人员无需引入任何JAR包，而且Android也针对SQLite封装了专属的API，调用起来非常快捷方便。   我也是第一次接触S
  • impala-2.1.2-CDH5.3.2 dayutianfei impala
    最近在整理impala编译的东西，简单记录几个要点： 根据官网的信息（https://github.com/cloudera/Impala/wiki/How-to-build-Impala）： 1. 首次编译impala，推荐使用命令： ${IMPALA_HOME}/buildall.sh -skiptests -build_shared_libs -format 2.仅编译BE ${I
  • 求二进制数中1的个数 周凡杨 java算法二进制
    解法一： 对于一个正整数如果是偶数，该数的二进制数的最后一位是 0 ，反之若是奇数，则该数的二进制数的最后一位是 1 。因此，可以考虑利用位移、判断奇偶来实现。   public int bitCount(int x){ int count = 0; while(x!=0){ if(x%2!=0){ /
  • spring中hibernate及事务配置 g21121 Hibernate
    hibernate的sessionFactory配置： <!-- hibernate sessionFactory配置 --> <bean id="sessionFactory" class="org.springframework.orm.hibernate3.LocalSessionFactoryBean"> <
  • log4j.properties 使用 510888780 log4j
    log4j.properties 使用 一.参数意义说明 输出级别的种类 ERROR、WARN、INFO、DEBUG ERROR 为严重错误 主要是程序的错误 WARN 为一般警告，比如session丢失 INFO 为一般要显示的信息，比如登录登出 DEBUG 为程序的调试信息 配置日志信息输出目的地 log4j.appender.appenderName = fully.qua
  • Spring mvc-jfreeChart柱图（2） 布衣凌宇 jfreechart
    上一篇中生成的图是静态的，这篇将按条件进行搜索，并统计成图表，左面为统计图，右面显示搜索出的结果。 第一步：导包 第二步；配置web.xml(上一篇有代码) 建BarRenderer类用于柱子颜色 import java.awt.Color; import java.awt.Paint; import org.jfree.chart.renderer.category.BarR
  • 我的spring学习笔记14-容器扩展点之PropertyPlaceholderConfigurer aijuans Spring3
    PropertyPlaceholderConfigurer是个bean工厂后置处理器的实现，也就是BeanFactoryPostProcessor接口的一个实现。关于BeanFactoryPostProcessor和BeanPostProcessor类似。我会在其他地方介绍。 PropertyPlaceholderConfigurer可以将上下文（配置文件）中的属性值放在另一个单独的标准java
  • maven 之 cobertura 简单使用 antlove maventestunitcoberturareport
    1. 创建一个maven项目 2. 创建com.CoberturaStart.java package com; public class CoberturaStart { public void helloEveryone(){ System.out.println("=================================================
  • 程序的执行顺序 百合不是茶 JAVA执行顺序
          刚在看java核心技术时发现对java的执行顺序不是很明白了,百度一下也没有找到适合自己的资料,所以就简单的回顾一下吧   代码如下;     经典的程序执行面试题 //关于程序执行的顺序 //例如： //定义一个基类 public class A(){ public A(
  • 设置session失效的几种方法 bijian1013 web.xmlsession失效监听器
    在系统登录后，都会设置一个当前session失效的时间，以确保在用户长时间不与服务器交互，自动退出登录，销毁session。具体设置很简单，方法有三种：（1）在主页面或者公共页面中加入：session.setMaxInactiveInterval(900);参数900单位是秒，即在没有活动15分钟后，session将失效。这里要注意这个session设置的时间是根据服务器来计算的，而不是客户端。所
  • java jvm常用命令工具 bijian1013 javajvm
    一.概述         程序运行中经常会遇到各种问题，定位问题时通常需要综合各种信息，如系统日志、堆dump文件、线程dump文件、GC日志等。通过虚拟机监控和诊断工具可以帮忙我们快速获取、分析需要的数据，进而提高问题解决速度。 本文将介绍虚拟机常用监控和问题诊断命令工具的使用方法，主要包含以下工具:       &nbs
  • 【Spring框架一】Spring常用注解之Autowired和Resource注解 bit1129 Spring常用注解
    Spring自从2.0引入注解的方式取代XML配置的方式来做IOC之后，对Spring一些常用注解的含义行为一直处于比较模糊的状态，写几篇总结下Spring常用的注解。本篇包含的注解有如下几个： Autowired Resource Component Service Controller Transactional 根据它们的功能、目的，可以分为三组，Autow
  • mysql 操作遇到safe update mode问题 bitray update
        我并不知道出现这个问题的实际原理,只是通过其他朋友的博客,文章得知的一个解决方案,目前先记录一个解决方法,未来要是真了解以后,还会继续补全.     在mysql5中有一个safe update mode,这个模式让sql操作更加安全,据说要求有where条件,防止全表更新操作.如果必须要进行全表操作,我们可以执行 SET
  • nginx_perl试用 ronin47 nginx_perl试用
    因为空闲时间比较多，所以在CPAN上乱翻，看到了nginx_perl这个项目(原名Nginx::Engine)，现在托管在github.com上。地址见：https://github.com/zzzcpan/nginx-perl 这个模块的目的，是在nginx内置官方perl模块的基础上，实现一系列异步非阻塞的api。用connector/writer/reader完成类似proxy的功能（这里
  • java-63-在字符串中删除特定的字符 bylijinnan java
    public class DeleteSpecificChars { /** * Q 63 在字符串中删除特定的字符 * 输入两个字符串，从第一字符串中删除第二个字符串中所有的字符。 * 例如，输入”They are students.”和”aeiou”，则删除之后的第一个字符串变成”Thy r stdnts.” */ public static voi
  • EffectiveJava--创建和销毁对象 ccii 创建和销毁对象
    本章内容： 1. 考虑用静态工厂方法代替构造器 2. 遇到多个构造器参数时要考虑用构建器（Builder模式） 3. 用私有构造器或者枚举类型强化Singleton属性 4. 通过私有构造器强化不可实例化的能力 5. 避免创建不必要的对象 6. 消除过期的对象引用 7. 避免使用终结方法 1. 考虑用静态工厂方法代替构造器     类可以通过
  • [宇宙时代]四边形理论与光速飞行 comsci
       从四边形理论来推论 为什么光子飞船必须获得星光信号才能够进行光速飞行？    一组星体组成星座  向空间辐射一组由复杂星光信号组成的辐射频带，按照四边形-频率假说  一组频率就代表一个时空的入口    那么这种由星光信号组成的辐射频带就代表由这些星体所控制的时空通道，该时空通道在三维空间的投影是一
  • ubuntu server下python脚本迁移数据 cywhoyi pythonKettlepymysqlcx_Oracleubuntu server
    因为是在Ubuntu下，所以安装python、pip、pymysql等都极其方便，sudo apt-get install pymysql， 但是在安装cx_Oracle（连接oracle的模块）出现许多问题，查阅相关资料，发现这边文章能够帮我解决，希望大家少走点弯路。http://www.tbdazhe.com/archives/602 1.安装python 2.安装pip、pymysql
  • Ajax正确但是请求不到值解决方案 dashuaifu Ajaxasync
    Ajax正确但是请求不到值解决方案   解决方案：1 .     async: false ,    2.     设置延时执行js里的ajax或者延时后台java方法！！！！！！！   例如：   $.ajax({     &
  • windows安装配置php+memcached dcj3sjt126com PHPInstallmemcache
    Windows下Memcached的安装配置方法 1、将第一个包解压放某个盘下面，比如在c:\memcached。 2、在终端（也即cmd命令界面）下输入 'c:\memcached\memcached.exe -d install' 安装。 3、再输入： 'c:\memcached\memcached.exe -d start' 启动。（需要注意的: 以后memcached将作为windo
  • iOS开发学习路径的一些建议 dcj3sjt126com ios
    iOS论坛里有朋友要求回答帖子，帖子的标题是： 想学IOS开发高阶一点的东西，从何开始，然后我吧啦吧啦回答写了很多。既然敲了那么多字，我就把我写的回复也贴到博客里来分享，希望能对大家有帮助。欢迎大家也到帖子里讨论和分享，地址：http://bbs.csdn.net/topics/390920759   下面是我回复的内容：   结合自己情况聊下iOS学习建议，
  • Javascript闭包概念 fanfanlovey JavaScript闭包
    1.参考资料 http://www.jb51.net/article/24101.htm http://blog.csdn.net/yn49782026/article/details/8549462 2.内容概述 要理解闭包，首先需要理解变量作用域问题 内部函数可以饮用外面全局变量 var n=999; 　　functio
  • yum安装mysql5.6 haisheng mysql
    1、安装http://dev.mysql.com/get/mysql-community-release-el7-5.noarch.rpm   2、yum install mysql   3、yum install mysql-server   4、vi /etc/my.cnf   添加character_set_server=utf8
  • po/bo/vo/dao/pojo的详介 IT_zhlp80 javaBOVODAOPOJOpo
        JAVA几种对象的解释 PO:persistant object持久对象,可以看成是与数据库中的表相映射的java对象。最简单的PO就是对应数据库中某个表中的一条记录，多个记录可以用PO的集合。PO中应该不包含任何对数据库的操作. VO:value object值对象。通常用于业务层之间的数据传递，和PO一样也是仅仅包含数据而已。但应是抽象出的业务对象,可
  • java设计模式 kerryg java设计模式
    设计模式的分类：    一、 设计模式总体分为三大类： 1、创建型模式（5种）：工厂方法模式，抽象工厂模式，单例模式，建造者模式，原型模式。 2、结构型模式（7种）：适配器模式，装饰器模式，代理模式，外观模式，桥接模式，组合模式，享元模式。 3、行为型模式（11种）：策略模式，模版方法模式，观察者模式，迭代子模式，责任链模式，命令模式，备忘录模式，状态模式，访问者
  • [1]CXF3.1整合Spring开发webservice——helloworld篇 木头.java springwebserviceCXF
    Spring 版本3.2.10 CXF 版本3.1.1 项目采用MAVEN组织依赖jar 我这里是有parent的pom，为了简洁明了，我直接把所有的依赖都列一起了，所以都没version，反正上面已经写了版本 <project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="ht
  • Google 工程师亲授：菜鸟开发者一定要投资的十大目标 qindongliang1922 工作感悟人生
    身为软件开发者，有什么是一定得投资的？ Google 软件工程师 Emanuel Saringan 整理了十项他认为必要的投资，第一项就是身体健康，英文与数学也都是必备能力吗？来看看他怎么说。（以下文字以作者第一人称撰写）） 你的健康 无疑地，软件开发者是世界上最久坐不动的职业之一。 每天连坐八到十六小时，休息时间只有一点点，绝对会让你的鲔鱼肚肆无忌惮的生长。肥胖容易扩大罹患其他疾病的风险，
  • linux打开最大文件数量1,048,576 tianzhihehe clinux
    File descriptors are represented by the C int type. Not using a special type is often  considered odd, but is, historically, the Unix way. Each Linux process has a maximum number of files th
  • java语言中PO、VO、DAO、BO、POJO几种对象的解释 衞酆夼 javaVOBOPOJOpo
    PO:persistant object持久对象 最形象的理解就是一个PO就是数据库中的一条记录。好处是可以把一条记录作为一个对象处理，可以方便的转为其它对象。可以看成是与数据库中的表相映射的java对象。最简单的PO就是对应数据库中某个表中的一条记录，多个记录可以用PO的集合。PO中应该不包含任何对数据库的操作。 BO:business object业务对象 封装业务逻辑的java对象
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他