用deepseek学大模型08-长短时记忆网络 (LSTM)

deepseek.com 从入门到精通长短时记忆网络(LSTM),着重介绍的目标函数，损失函数，梯度下降 标量和矩阵形式的数学推导，pytorch真实能跑的代码案例以及模型,数据， 模型应用场景和优缺点，及如何改进解决及改进方法数据推导。

从入门到精通长短时记忆网络 (LSTM)

参考：长短时记忆网络（LSTM）在序列数据处理中的优缺点分析

---

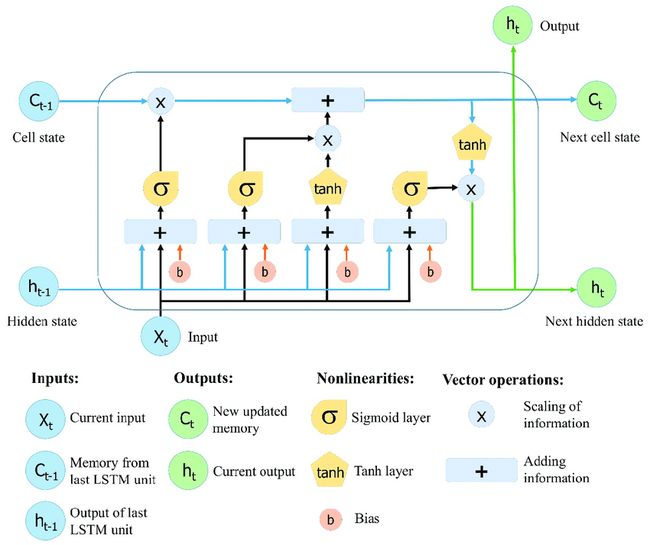
1. LSTM 核心机制

LSTM 通过门控机制（遗忘门、输入门、输出门）和细胞状态（Cell State）解决 RNN 的梯度消失问题。

核心公式（时间步$t$）：

1. 遗忘门（Forget Gate）：
   $${\mathbf{f}}_t=\sigma \left({\mathbf{W}}_f[{\mathbf{h}}_{t-1},{\mathbf{x}}_t]+{\mathbf{b}}_f\right)$$
2. 输入门（Input Gate）：
   $${\mathbf{i}}_t=\sigma \left({\mathbf{W}}_i[{\mathbf{h}}_{t-1},{\mathbf{x}}_t]+{\mathbf{b}}_i\right)$$
   $${\tilde{\mathbf{C}}}_t=\tanh \left({\mathbf{W}}_C[{\mathbf{h}}_{t-1},{\mathbf{x}}_t]+{\mathbf{b}}_C\right)$$
3. 细胞状态更新：
   $${\mathbf{C}}_t={\mathbf{f}}_t\odot {\mathbf{C}}_{t-1}+{\mathbf{i}}_t\odot {\tilde{\mathbf{C}}}_t$$
4. 输出门（Output Gate）：
   $${\mathbf{o}}_t=\sigma \left({\mathbf{W}}_o[{\mathbf{h}}_{t-1},{\mathbf{x}}_t]+{\mathbf{b}}_o\right)$$
   $${\mathbf{h}}_t={\mathbf{o}}_t\odot \tanh ({\mathbf{C}}_t)$$

---

2. 目标函数与损失函数

• 目标函数：最小化预测与真实值的差异（监督学习）。
• 损失函数（以分类任务交叉熵为例）：
  $$L=-\frac{1}{T}\sum _{t=1}^T\sum _{c=1}^C{\hat{\mathbf{y}}}_{t,c}\log ({\mathbf{y}}_{t,c})$$
  其中$C$为类别数，$\hat{\mathbf{y}}$为真实标签的 one-hot 编码。

---

3. 梯度下降与数学推导

LSTM 的梯度反向传播通过细胞状态${\mathbf{C}}_t$和门控机制稳定梯度流动。

标量形式推导（以遗忘门${\mathbf{f}}_t$为例）：
$$\frac{\partial L}{\partial {\mathbf{f}}_t}=\frac{\partial L}{\partial {\mathbf{h}}_t}\cdot \frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{C}}_t}\cdot \frac{\partial {\mathbf{C}}_t}{\partial {\mathbf{f}}_t}$$
其中：
$$\frac{\partial {\mathbf{C}}_t}{\partial {\mathbf{f}}_t}={\mathbf{C}}_{t-1}\odot {\mathbf{f}}_t\odot (1-{\mathbf{f}}_t)$$

矩阵形式推导（链式法则）：
$$\frac{\partial L}{\partial {\mathbf{W}}_f}=\sum _{t=1}^T\left({\delta }_{f,t}\cdot [{\mathbf{h}}_{t-1},{\mathbf{x}}_t{]}^T\right)$$
其中${\delta }_{f,t}$为遗忘门的梯度误差：
$${\delta }_{f,t}=\frac{\partial L}{\partial {\mathbf{f}}_t}\odot {\sigma }^{\prime }(\cdot )$$

---

4. PyTorch 代码案例

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 数据生成：正弦波 + 噪声
time = torch.arange(0, 100, 0.1)
data = torch.sin(time) + 0.1 * torch.randn(len(time))

# 转换为序列数据（窗口长度=20）
def create_sequences(data, seq_length=20):
    X, y = [], []
    for i in range(len(data)-seq_length):
        X.append(data[i:i+seq_length])
        y.append(data[i+seq_length])
    return torch.stack(X).unsqueeze(-1), torch.stack(y).unsqueeze(-1)

X, y = create_sequences(data)
X_train, y_train = X[:800], y[:800]  # 划分训练集和测试集
X_test, y_test = X[800:], y[800:]

# 定义 LSTM 模型
class LSTMModel(nn.Module):
    def __init__(self, input_size=1, hidden_size=64, output_size=1):
        super().__init__()
        self.lstm = nn.LSTM(input_size, hidden_size, batch_first=True)
        self.fc = nn.Linear(hidden_size, output_size)
    
    def forward(self, x):
        out, (h_n, c_n) = self.lstm(x)  # out: (batch, seq_len, hidden_size)
        out = self.fc(out[:, -1, :])    # 取最后一个时间步
        return out

model = LSTMModel()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

# 训练
epochs = 100
train_loss = []
for epoch in range(epochs):
    optimizer.zero_grad()
    outputs = model(X_train)
    loss = criterion(outputs, y_train)
    loss.backward()
    nn.utils.clip_grad_norm_(model.parameters(), 0.5)  # 梯度裁剪
    optimizer.step()
    train_loss.append(loss.item())

# 可视化训练损失
plt.plot(train_loss)
plt.title("Training Loss")
plt.show()

# 预测
model.eval()
with torch.no_grad():
    train_pred = model(X_train)
    test_pred = model(X_test)

# 绘制结果
plt.figure(figsize=(12, 5))
plt.plot(data.numpy(), label="True Data")
plt.plot(range(20, 820), train_pred.numpy(), label="Train Predictions")
plt.plot(range(820, len(data)), test_pred.numpy(), label="Test Predictions")
plt.legend()
plt.show()

---

5. 应用场景与优缺点

• 应用场景：
  • 时间序列预测（股票价格、天气）
  • 自然语言处理（文本生成、机器翻译）
  • 语音识别
• 优点：
  • 解决长程依赖问题
  • 通过门控机制稳定梯度流动
  • 可处理变长序列
• 缺点：
  • 计算复杂度高（参数多）
  • 对短序列可能过拟合
  • 训练时间较长

---

6. 改进方法及数学推导

1. GRU（门控循环单元）
   简化 LSTM，合并遗忘门和输入门：
   $${\mathbf{z}}_t=\sigma ({\mathbf{W}}_z[{\mathbf{h}}_{t-1},{\mathbf{x}}_t])$$
   $${\mathbf{r}}_t=\sigma ({\mathbf{W}}_r[{\mathbf{h}}_{t-1},{\mathbf{x}}_t])$$
   $${\tilde{\mathbf{h}}}_t=\tanh (\mathbf{W}[{\mathbf{r}}_t\odot {\mathbf{h}}_{t-1},{\mathbf{x}}_t])$$
   $${\mathbf{h}}_t=(1-{\mathbf{z}}_t)\odot {\mathbf{h}}_{t-1}+{\mathbf{z}}_t\odot {\tilde{\mathbf{h}}}_t$$

2. 双向 LSTM（Bi-LSTM）
   同时捕捉前向和后向依赖：
   $${\mathbf{h}}_t=\text{LSTM}({\mathbf{x}}_t,{\mathbf{h}}_{t-1})$$
   $${\mathbf{h}}_t=\text{LSTM}({\mathbf{x}}_t,{\mathbf{h}}_{t+1})$$
   $${\mathbf{h}}_t=[{\mathbf{h}}_t,{\mathbf{h}}_t]$$

3. 注意力机制
   增强对关键时间步的关注：
   $${\alpha }_t=\text{softmax}({\mathbf{v}}^T\tanh ({\mathbf{W}}_h{\mathbf{h}}_t+{\mathbf{W}}_s\mathbf{s}))$$
   $$\mathbf{c}=\sum _{t=1}^T{\alpha }_t{\mathbf{h}}_t$$

---

7. 关键改进的数学验证（以 GRU 为例）

• 梯度稳定性：
  GRU 的更新门${\mathbf{z}}_t$控制历史信息的保留比例，梯度可沿两条路径传播：
  $$\frac{\partial {\mathbf{h}}_t}{\partial {\mathbf{h}}_{t-1}}=(1-{\mathbf{z}}_t)+{\mathbf{z}}_t\odot \frac{\partial {\tilde{\mathbf{h}}}_t}{\partial {\mathbf{h}}_{t-1}}$$
  避免传统 RNN 的连乘梯度。

---

通过上述内容，您可全面掌握 LSTM 的理论基础、实际实现及优化方法。