noip 2017 做题记录
noip 2017
小凯的疑惑
最大不可表数。
以前写过 这篇博客
时间复杂度
恶心的模拟题……
推荐食用洛谷第一篇题解,写的很好。
getline 简要讲解
读入一个单词时,可用 cin/scanf。读入一行带空格的字符时,可用getline。(我只会这几个,而且它们用起来比较方便因为我太懒了 )。
我写的与洛谷题解稍有不同,因为他读入字符串的方法感觉很高级其实是看不懂 。
#include逛公园
30分数据:
当 k=0 时,问题转化为从1到 n 的最短路有多少条,转化为 最短路计数 这道题,只需在原有的spfa上稍作改动,在松弛节点时用sum数组计数:
if(d[v]>d[u]+1)
{
d[v]=d[u]+1;
sum[v]=sum[u]%mod;
if(!inq[v])
{
inq[v]=1;
q.push(v);
}
}
else if(d[v]==d[u]+1)
{
sum[v]=(sum[u]+sum[v])%mod;
}
正解:
建反图跑一遍最短路,d[u] 表示从 u 到 n 的最短路长度。
记忆化搜索,f[u][r] 表示从 u 到 n 的路径中,与 d[u] 长度差不超过 r的路径数量。则最终答案即为 f[1][k] 。
对一个点 u,它的 f[u][r] 由每个出点 v 更新而来。而每条由 n 到 v 再到 u 的路径在经过边(u,v)后与 d[u] 的差会增加 d[v]+w(边(u,v)的长度)-d[u],所以限制了所有走到 v 的路径长度不得超过r-d[v]+w-d[u],故:
f[u][r] = ∑ f[v][r-d[v]+w-d[u]]。当 u=n 时f[u][r]=1。
因为图中有0环,所以用数组 in[u][r] 标记来判断由 u 是否会走到自己且路径长度不变。在搜索完 u 之后清除标记。
部分题解对0环的处理是错误的,建议在水完洛谷的经验后 到 UOJ 提交程序以验证正确性。
#include奶酪
做法一:并查集
用两个数组分别存储与上切面相交(相切),与下切面相交(相切)的空洞。在读入数据时将相交或相切的洞两两合并祖先。最后查询上述两个数组中是否有元素的并查集祖先相同,表明可以从下切面走到上切面。
(以前的马蜂有点丑虽然现在也不咋地 )
#include做法二:搜索
从每个与下切面相交或相切的空洞出发,走向一个未被标记过的且二者距离小于等于二倍半径的空洞。若能走到一个与上切面相切或相交的空洞则返回。
这样做跑的很快,应该是因为用来标记节点的vis数组的功劳。
#include宝藏
45分:prim求最小生成树,按每个点的L×K,即 “道路的长度” 乘以 “赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的宝藏屋的数量” 排序,贪心即可。
#include100分:搜索剪枝
用二维数组 d 存边,由于可能有重边,所以取最小的边权。t 数组存每个节点所连的节点个数。tar 数组辅助存边,tar[u][i] 数组表示与 u 点相连的第 i 条边。预处理将tar 排序,使每个点所连的边的按从小到大的顺序以便贪心减少搜索量。
r 数组存搜索时已经经过的点。lev 数组存这些点的深度,即起点到该宝藏屋经过的宝藏屋数量。变量 tot 存当前答案。
用tmp存由当前点搜索下去的最小可能边权和,即剩下未经过的点中,各自所连的最短的边的权值和。这个变量是用来给搜索剪枝,到当前节点 u 时,最小的可能答案即为 tmplev[u],若 tot+tmplev[u] 已经大于了先前算出的答案,则直接返回。
大概模拟一下搜索过程:
设最终答案为这样一棵树,从一号点开始搜索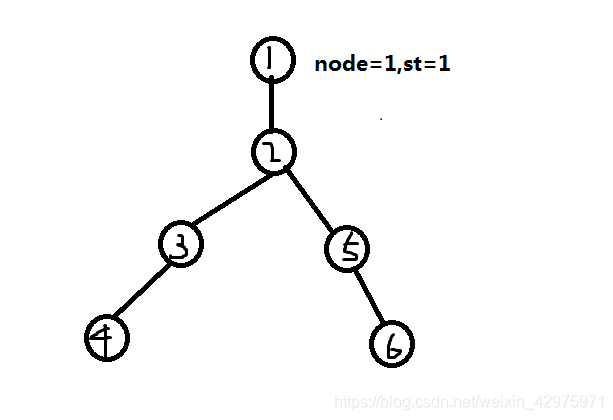
与它相连的点只有二号点,来到二号点
,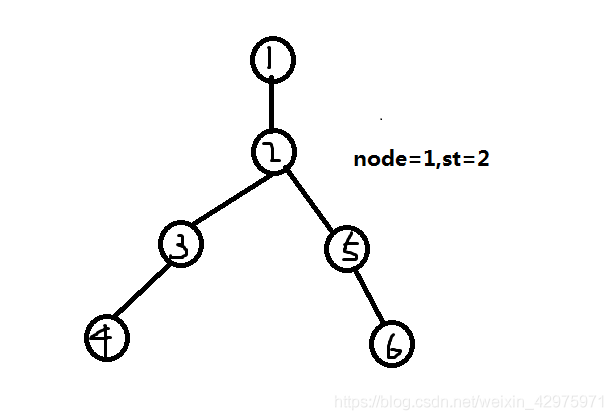
此时node为1,st为2,但1号点无其它连边,所以开始枚举2号点的子节点,到达3号点
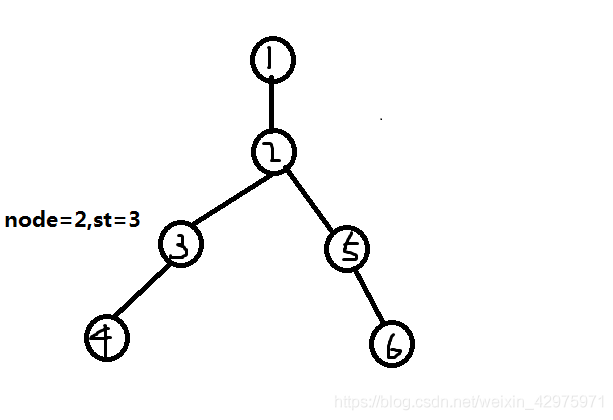
此时node为2,st为3,但此时2号点还有其他子节点,即tar[i][j]还有值,所以下一步搜索5号点。
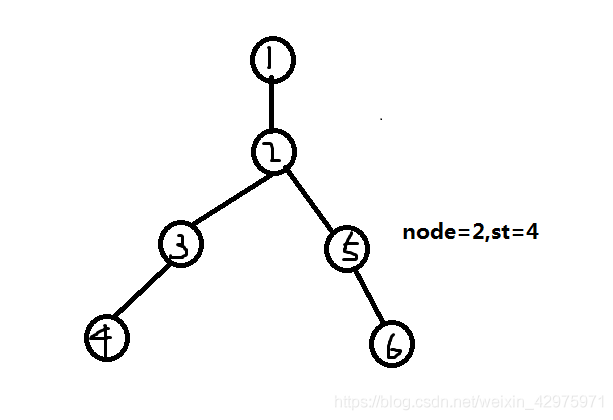
2号点已无子节点,搜素下一个node,即node=3的子节点,来到4号点。
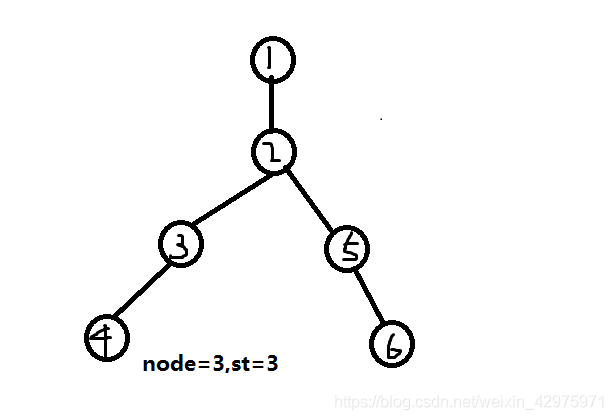
然后搜索到是6号点,搜索完成。
建议自己造组数据跑一遍。蒟蒻自己人脑模拟时总感觉答案情况跑不完。实际调试后才明白搜索顺序。
模拟后可知之后搜索到的点的深度一定不小于当前点,所以tmp*当前点的lev 值一定小于等于正确答案中剩余节点的所连边的边权值和乘以深度。这个剪枝是正确的。
(代码注释来自洛谷题解)
#include列队
线段树动态开点,太坑了,我不会。
大意就是给每行的前m-1个点建树,另外给第m列建一棵树。模拟过程加点,查询,在查询节点时顺便减去该点,表明这个人已经离队。
因为线段树不能删点,所以要预先开足够的点。用siz数组储存这个节点包含的区间内还有多少人。在一个人离队时所有包含这个区间的节点的siz值减1,表明该区间的人数减少。一个人归队时就将其插入相应列(行)的最后。用tot数组表明该行(列)末尾归队过多少人,便于插入操作。
一个细节是,查询(query)操作时我们要找的是第几个人,而有些线段树节点是空的,因为该位置的人已经离队。查询时判断目标位置在左右子树时要与左子树的siz比较,若该子树的id未被更新过,表明前面的人都没离过队,siz即为mid-l+1。而插入(update)操作时可直接用线段树下标进行判断,因为这个人一定是站在某一行(某一列)的最后。
#include