HDU 1055 Color a Tree 【贪心】

传送门：HDU 1055

---

Color a Tree Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)

Problem Description
Bob is very interested in the data structure of a tree. A tree is a directed graph in which a special node is singled out, called the “root” of the tree, and there is a unique path from the root to each of the other nodes.
Bob intends to color all the nodes of a tree with a pen. A tree has N nodes, these nodes are numbered 1, 2, …, N. Suppose coloring a node takes 1 unit of time, and after finishing coloring one node, he is allowed to color another. Additionally, he is allowed to color a node only when its father node has been colored. Obviously, Bob is only allowed to color the root in the first try.
Each node has a “coloring cost factor”, Ci. The coloring cost of each node depends both on Ci and the time at which Bob finishes the coloring of this node. At the beginning, the time is set to 0. If the finishing time of coloring node i is Fi, then the coloring cost of node i is Ci * Fi.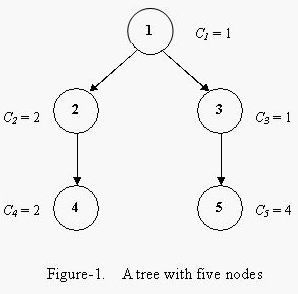
For example, a tree with five nodes is shown in Figure-1. The coloring cost factors of each node are 1, 2, 1, 2 and 4. Bob can color the tree in the order 1, 3, 5, 2, 4, with the minimum total coloring cost of 33.
Given a tree and the coloring cost factor of each node, please help Bob to find the minimum possible total coloring cost for coloring all the nodes.

Input
The input consists of several test cases. The first line of each case contains two integers N and R (1 <= N <= 1000, 1 <= R <= N), where N is the number of nodes in the tree and R is the node number of the root node. The second line contains N integers, the i-th of which is Ci (1 <= Ci <= 500), the coloring cost factor of node i. Each of the next N-1 lines contains two space-separated node numbers V1 and V2, which are the endpoints of an edge in the tree, denoting that V1 is the father node of V2. No edge will be listed twice, and all edges will be listed.
A test case of N = 0 and R = 0 indicates the end of input, and should not be processed.

Output
For each test case, output a line containing the minimum total coloring cost required for Bob to color all the nodes.

Sample Input
5 1
1 2 1 2 4
1 2
1 3
2 4
3 5
0 0

Sample Output
33

---

题意：
一棵树，结点树为n ，根结点为r 。 每个结点都有一个权值ci ，开始时间为0 ，每染色一个结点需要耗时1 ，每个结点的染色代价为ci*ti （ ti为当前的时间），每个结点只有在父结点已经被染色的条件下才能被染色。 求染完整棵树需要花费的最小代价。


题解：

这题看了一个晚上都没看出来个什么，第二天早上动手模拟了一下才有所理解。
其实贪心的方案很好想，无非就是权值ci越大的点先染色所花代价最小，而要想给它染色首先他的父亲结点必须已经染完色，同样的，如果这点的父亲结点已经染色，那么下一个要染色的点一定是它。

关键在于如何实现它。看了别人的博客，终于弄懂了点：

利用并查集的思想（只利用了“并”的思想）。既然当前染色点和他的父结点的染色顺序一定相邻，所以两个结点可以结合在一起，把他们看作一个新的结点。

1. 建立结构体node ，结构体数组 points[i] 表示i结点的状态， points[i].c=ci 为权值， points[i].w=ci 为当前权值， points[i].t=1 为经过这个结点需要的耗时（也可以理解为这个结点包含几个合并的结点），points[i].fa 为父结点

2. 找到一个最大权值非根结点pos，将其与其父亲fa合并形成一个新的结点，新结点是父亲fa的位置，如果有节点与pos相连，让它指向pos的父节点；
   答案 ans+= points[pos].c * points[fa].t ，表示经过父节点fa后，需要经历 points[fa].t 时间才到达pos ，所以将pos同fa合并后，总代价要加上这段路径的代价；
   新结点的情况 : points[fa].c+=points[pos].c , points[fa].t+=points[pos].t,
   points[fa].w=1.0* points[fa].c / points[fa].t
   (新结点权值变成算术平均值，因为到这个结点的代价被平分分给t个结点）。

3. 重复 2 直到结点只有一个为止，应进行n-1次。

初始时使ans = sum(c[i]),序列中的t都置为1，w置为c；

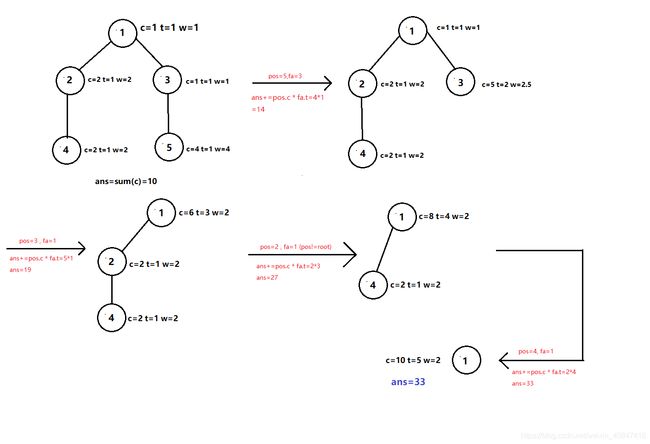
样例模拟过程：

这里给出一组例子，动手模拟试试：

6 1
1 2 1 3 4 1
1 2
1 3
2 4
3 5
5 6

结果为：44

---

AC代码：

#include
#include
#include
#include
#include
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int N=1000+10;
int n,r;
struct Node
{
  int c;//权值
  int t;//步数
  int fa;//父亲结点
  double w;
}points[N];

int find()//找最大权值的点
{
  int pos;
  double maxn=0;
  for(int i=1;i<=n;i++)
  {
    if(points[i].w>maxn&&i!=r)
    {
      pos=i;
      maxn=points[i].w;
    }
  }
  return pos;
}

int main()
{
  while(scanf("%d%d",&n,&r)&&n&&r)
  {
    int x,y;
    int ans=0;
    for(int i=1;i<=n;i++)
    {
      scanf("%d",&points[i].c);
      points[i].w=points[i].c;
      points[i].t=1;
      points[i].fa=i;
      ans+=points[i].c;
    }
    for(int i=1;i<n;i++)
    {
      scanf("%d%d",&x,&y);
      points[y].fa=x;
    }
    for(int i=1;i<n;i++)
    {
      int pos=find();
      int fa=points[pos].fa;
      points[pos].w=0;
      ans+=points[pos].c*points[fa].t;
      for(int j=1;j<=n;j++)
      {
        if(points[j].fa==pos)
          points[j].fa=fa;
      }
      points[fa].c+=points[pos].c;
      points[fa].t+=points[pos].t;
      points[fa].w=points[fa].c*1.0/points[fa].t*1.0;
    }
    printf("%d\n",ans);
  }
  return 0;
}