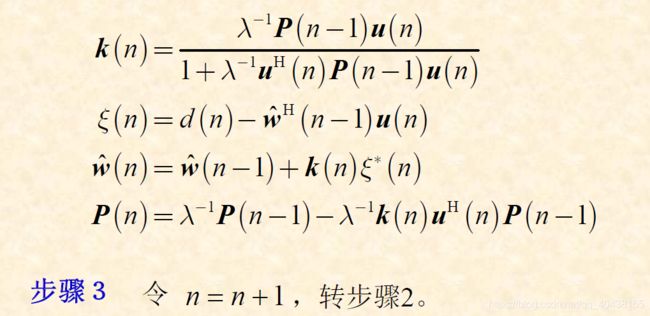现代数字信号处理第六章——最小二乘理论和算法
本章核心:利用最小二乘估计及算法,根据有限个数的观测数据寻求滤波器的最优值。内容分为四部分:
- 最小二乘估计原理
- 基于奇异值分解的最小二乘法求解
- 基于最小二乘的FBLP谱估计
- 最小二乘的两种递归算法:RLS和QR-RLS
一、最小二乘理论
1、线性方程组 A x = b Ax=b Ax=b解的形式
- A可逆, x = A − 1 b x=A^{-1}b x=A−1b
- A列满秩,独立方程数大于未知量数,方程有最小二乘解, x ^ L S = ( A H A ) − 1 A H b \hat{x}_{LS}=(A^HA)^{-1}A^Hb x^LS=(AHA)−1AHb
- A行满秩,位置量数目大于方程数,方程有无穷多组解,但有唯一最小范数解, x ^ F = A H ( A A H ) − 1 b \hat{x}_{F}=A^H(AA^H)^{-1}b x^F=AH(AAH)−1b
2、LS估计的确定型正则方程
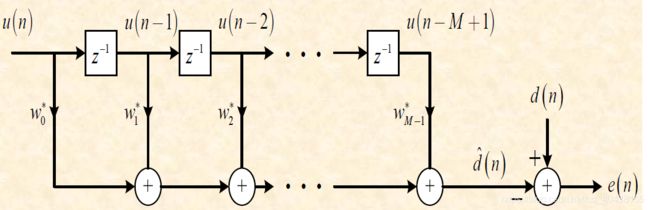
\quad 经过推导,令数据矩阵 A H A^H AH如下图所示,则估计值 b ^ = A w \hat{b}=Aw b^=Aw,误差为 e = b − b ^ = b − A w e=b-\hat{b}=b-Aw e=b−b^=b−Aw
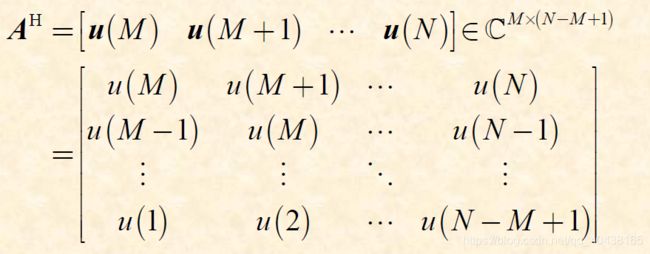
\quad 横向滤波器的设计原则是:寻找权向量使得误差信号 e ( n ) e(n) e(n)在某种意义下取得极小值。即 J = ∑ n = M N ∣ e ( n ) ∣ 2 = ∣ e ∣ 2 = e H e = ( b H − w H A H ) ( b − A w ) = b H b − b H A w − w H A H b − w H A H A w Δ J = − 2 A H b + 2 A H A w = 0 确 定 性 正 则 方 程 : A H A w ^ = A H b 最 小 二 乘 解 : w ^ = ( A H A ) − 1 A H b 最 小 二 乘 估 计 : b ^ = A w ^ , 简 称 L S 估 计 J=\sum_{n=M}^N|e(n)|^2=|e|^2=e^He\\=(b^H-w^HA^H)(b-Aw)\\=b^Hb-b^HAw-w^HA^Hb-w^HA^HAw\\\Delta J=-2A^Hb+2A^HAw=0\\确定性正则方程:A^HA\hat{w}=A^Hb\\最小二乘解:\hat{w}=(A^HA)^{-1}A^Hb\\最小二乘估计:\hat{b}=A\hat{w},简称LS估计 J=n=M∑N∣e(n)∣2=∣e∣2=eHe=(bH−wHAH)(b−Aw)=bHb−bHAw−wHAHb−wHAHAwΔJ=−2AHb+2AHAw=0确定性正则方程:AHAw^=AHb最小二乘解:w^=(AHA)−1AHb最小二乘估计:b^=Aw^,简称LS估计
3、LS估计正交原理
- A中每一列都与误差向量 e e e正交: A H e = A H ( b − A w ^ ) = A H b − A H A w ^ = 0 A^He=A^H(b-A\hat{w})=A^Hb-A^HA\hat{w}=0 AHe=AH(b−Aw^)=AHb−AHAw^=0
- 估计向量 b ^ 是 b \hat{b}是b b^是b的一个正交投影: b ^ e = b ^ ( b − A w ^ ) = 0 \hat{b}e=\hat{b}(b-A\hat{w})=0 b^e=b^(b−Aw^)=0
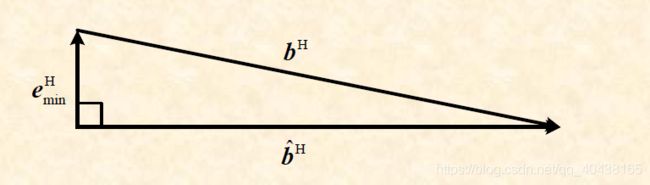
4、代价函数极小值 J m i n = e m i n H e m i n J_{min}=e^H_{min}e_{min} Jmin=eminHemin
二、LS问题的求解——奇异值分解
\quad 直接求解 A H A w ^ = A H b A^HA\hat{w}=A^Hb AHAw^=AHb工程上不易实现。我们借助奇异值分解可以求出 A H A A^HA AHA的 逆。假设 A A A含有 M M M个非零特征值 ∑ = { σ 1 , σ 2 , ⋯ , σ M } \sum=\{\sigma_1,\sigma_2,\cdots,\sigma_M\} ∑={σ1,σ2,⋯,σM},可以将 A H A A^HA AHA分解为酉矩阵 X X X的表达式 A H A = X ∑ 2 X H A^HA=X\sum^2X^H AHA=X∑2XH,因为酉矩阵 X − 1 = X X^{-1}=X X−1=X,可得 ( A H A ) − 1 = X ∑ − 2 X H (A^HA)^{-1}=X\sum^{-2}X^H (AHA)−1=X∑−2XH,展开可得:
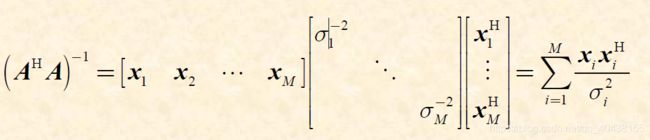
故而, w ^ = ∑ i = 1 M x i x i H σ i 2 A H b \hat{w}=\sum_{i=1}^M\frac{x_ix_i^H}{\sigma_i^2}A^Hb w^=∑i=1Mσi2xixiHAHb。利用SVD得到LS问题的算法如下:

三、基于LS估计的FBLP原理和功率谱估计
\quad 对于FLP而言,数据矩阵为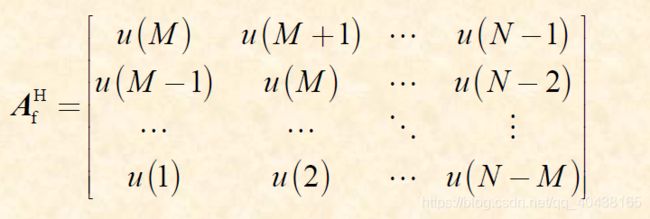
代价函数为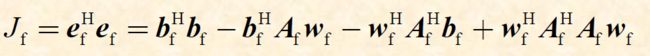
对于BLP而言,数据矩阵和代价函数依次是:
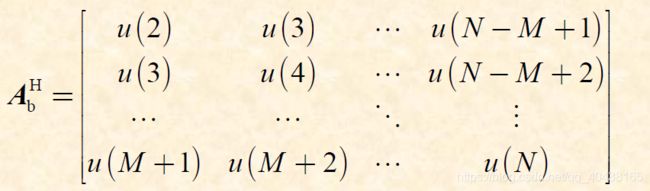
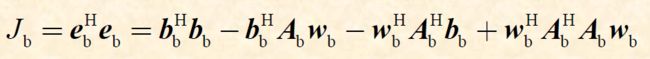
\quad 令FBLP的代价函数为FLP和BLP之和,即 J = J f + J b J=J_f+J_b J=Jf+Jb,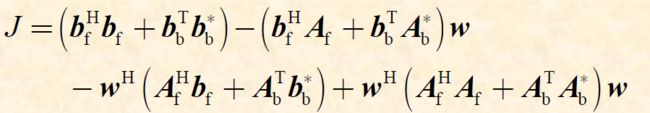
\quad 定义向量 b H = [ b f H , b b T ] , A H = [ A f H , A b T ] b^H=[b^H_f,b^T_b],A^H=[A^H_f,A^T_b] bH=[bfH,bbT],AH=[AfH,AbT],则 J = b H b − b H A w − w H A H b − w H A H A w J=b^Hb-b^HAw-w^HA^Hb-w^HA^HAw J=bHb−bHAw−wHAHb−wHAHAw,只需使得 A H A w = A H b A^HAw=A^Hb AHAw=AHb便能最小化误差。
使用SVD实现AR模型功率谱估计
四、递归最小二乘算法RLS
- 初值 δ = 0.001 , 0.01 , 0.1 \delta=0.001,0.01,0.1 δ=0.001,0.01,0.1对RLS算法影响很小
- λ \lambda λ的取值对算法有明显影响,主要表现在稳态误差上
- PLS算法比LMS算法收敛特性好很多

五、基于QR分解递归最小二乘算法QPLS
QR分解原理

e ( n ) = b ( n ) − A ( n ) w ( n ) J ( n ) = ∣ e ( n ) ∣ 2 引 入 遗 忘 因 子 λ = β 2 , J ( n ) = ∣ ∣ B ( n ) e ( n ) ∣ ∣ 2 , B ( n ) = d i a g { β n − 1 , β n − 2 , ⋯ , β , 1 } 酉 矩 阵 Q ( n ) 左 乘 , 得 J ( n ) = ∣ ∣ Q ( n ) B ( n ) e ( n ) ∣ ∣ 2 = ∣ ∣ Q ( n ) B ( n ) b ( n ) − Q ( n ) B ( n ) A ( n ) w ∣ ∣ 2 e(n)=b(n)-A(n)w(n)\\J(n)=|e(n)|^2\\引入遗忘因子\lambda=\beta^2,J(n)=||B(n)e(n)||^2,B(n)=diag\{\beta^{n-1},\beta^{n-2},\cdots,\beta,1\}\\酉矩阵Q(n)左乘,得J(n)=||Q(n)B(n)e(n)||^2=||Q(n)B(n)b(n)-Q(n)B(n)A(n)w||^2 e(n)=b(n)−A(n)w(n)J(n)=∣e(n)∣2引入遗忘因子λ=β2,J(n)=∣∣B(n)e(n)∣∣2,B(n)=diag{βn−1,βn−2,⋯,β,1}酉矩阵Q(n)左乘,得J(n)=∣∣Q(n)B(n)e(n)∣∣2=∣∣Q(n)B(n)b(n)−Q(n)B(n)A(n)w∣∣2
\quad 选择 Q ( n ) Q(n) Q(n)使得 Q ( n ) B ( n ) A ( n ) = [ R ( n ) , 0 ] T Q(n)B(n)A(n)=[R(n),0]^T Q(n)B(n)A(n)=[R(n),0]T,
\quad 使 Q ( n ) B ( n ) b ( n ) = [ p ( n ) , v ( n ) ] T Q(n)B(n)b(n)=[p(n),v(n)]^T Q(n)B(n)b(n)=[p(n),v(n)]T,则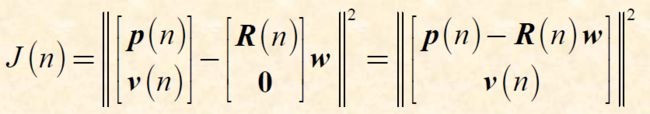
\quad 故而当 R ( n ) w = p ( n ) R(n)w=p(n) R(n)w=p(n)时 J ( n ) J(n) J(n)最小 J m i n = ∣ ∣ v ( n ) ∣ ∣ 2 J_{min}=||v(n)||^2 Jmin=∣∣v(n)∣∣2,并可求出权重向量

六、基于Givens旋转得QP-RLS算法
\quad 如何得到 Q ( n ) Q(n) Q(n),使得 Q ( n ) B ( n ) A ( n ) Q(n)B(n)A(n) Q(n)B(n)A(n)为上三角矩阵呢?借助Givens旋转可以实现。