计算机科学——图论专题

Content

一、图论基础

二、树

三、平面图

四、匹配理论

五、着色定理

六、欧拉图和哈密顿图

---

一、图论基础

1、图的定义：
G={V(G), E(G), ψ(G)}，其中，
V(G)：顶集合，非空
E(G)：边集合
ψ_G：从集合E(G)到V(G)×V(G)的一个映射，称为G的关联函数。若ψ_G(e)=(u, v)，则简写成e=uv，称u是有向边e的尾，v是有向边e的头
若顶集或边集有一个为无穷集合，则称G为无限图，否则为有限图。
根据边有无方向，分为有向图和无向图。无说明时，认为是无向图即可。

2、相关概念（一）：
（1）边的端点：e=uv时，称顶u和v是边e的端点
（2）边与顶相关联：若边e的端点是u与v，则称e与u, v相关联
（3）邻顶：同一条边的两个端点叫做邻顶
（4）邻边：与同一个顶相关联的两条边叫做邻边
（5）环：只与一个顶相关联的边叫做环
（6）重边：ψ_G(e₁)=ψ_G(e₂)=uv，则称e1与e2是重边
（7）单图：无环无重边的图
（8）空图：无边图
（9）完全图：任二顶皆相邻的单图，记之为K_ν
（10）二分图：V(G)=X∪Y，X∩Y=Ø，且X中任二顶不相邻，Y中任二顶不相邻，则称G为二分图
（11）完全二分图：若X中每个顶点皆与Y中一切顶相邻，记成K_m,n，其中m=|X|，n=|Y|
（12）星：K_1,n叫做星
（13）k次正则图：d(v) 恒等于k的图
（14）图的最小次 / 最大次
（15）图同构

3、相关概念（二）：
（1）边图：设G是一个图，L(G)是另一个图，且V(L(G))=E(G)，即L(G)中两顶点相邻当且仅当它们是G中的两条相邻的边。
性质：

• 若uv∈E(G)，则在L(G)中uv对应的顶的次数是d(u)+d(v)-2
• G≌L(G)当且仅当G是一个多边形

（2）

（3）

（4）图的直径和半径：
单图G中最长的圈之长称为该图的周长；最短的圈之长称为该图的围长；两顶点间距离中的最大值称为直径，记成d(G)，即


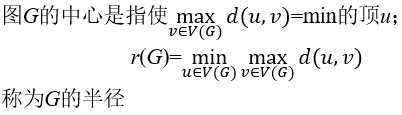
（5）图的补图：
单图G的补图记成G_c, G_c是这样一个图，V(G_c)=V(G)，当且仅当在G中两顶不相邻时，该二顶在G_c中相邻。它有一个定理：单图G与其补图不能都不连通。

4、基础定理：
（1）欧拉定理：

（2）欧拉定理的推论：
图中奇次顶总数是偶数

（3二分图判定：
图G是二分图当且仅当G中无奇圈

5、Dijkstra算法：
用于最短路径，如图。

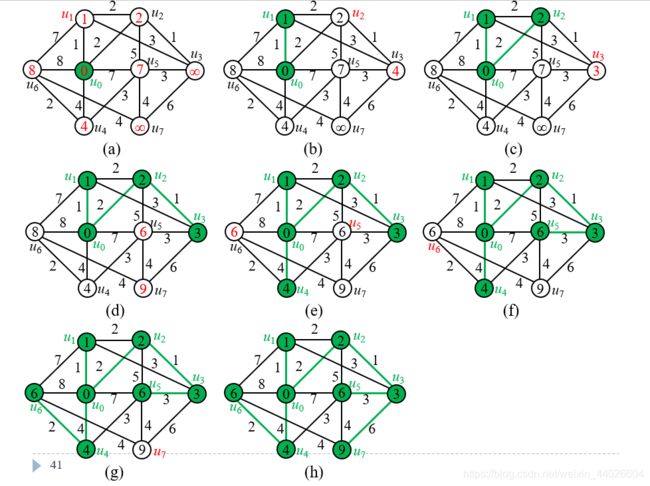
注：图论证明常用技巧：最长轨

---

二、树

1、定义：
无圈连通图称为树。每个连通片皆为树的不连通图称为森林；树上次数为1的顶称为叶；如果一个树T是图G的生成子图，则称T是G的生成树。G-E(T)称为树余

2、重要等价命题：
命题A G是树
命题B G中任二顶间恰有一条轨
命题C G中无圈，ε=ν-1
命题D G是连通图，ε=ν-1
命题E G是连通图，∀e∈E(G), G-e不连通
命题F G无圈，G+e恰含一个圈，其中e是任一不在E(G)中的以V(G)中的顶为端点的边

3、重要推论：
G是连通图的充分必要条件是G有生成树

4、生成树的个数(注意：以顶点序来区分生成树，而不考虑同构情况)
用τ(G)表示生成树个数，则：
τ(G) = n^n-2
一个与之相关的定理：
e是连通图G中的一条边，则τ(G)=τ(G-e)+τ(G•e)，其中G•e是把边e的长度收缩成零，e的两个端点重合成一个顶形成的图

5、求生成树——搜索算法： BFS / DFS
其中比较重要的一类生成树是最小生成树（也有人叫最优树），求解算法有Prim / Kruskal算法

6、有序树：
k∈N，若T是外向树，且任一顶v∈V(T), d+(v)≤k，则称T为k元树。 e∈E(T) ，T是外向树，e=uv，则称u是v之父，v是u之子（图示中父比子高）。同父之子称兄弟，兄弟有序时，称为有序树。有序树之序列称为有序林。有序树中较特殊，也是最常使用的是有序二元树，对有序二元树进行编码：
(i) 根不标码
(ii) 兄弟有序，左为兄，标0，右为弟，标1（编码即定位，0表示定位在左，1表示定位在右）
(iii) 从根始到叶的轨上依次抄出各顶之码，写在叶下方，称为该叶的前缀

在有序二元树中，存在最优二元树，它是所有同性质树中带权路径和最小的树（Huffman树）

7、n顶有序编码二元树的数目：
一个括号列是好括号列当且仅当它由一半右括号一半左括号组成，且从左向右看这个括号列时，看到的右括号不超过左括号个数

引入Catalan数：
由n个左括号组成的好括号列的个数为

n顶有序林与n顶有序编码二元树的数目皆c(n)

把不是叶的顶皆两个儿子的有序二元树称为典型有序二元树

---

三、平面图

1、平面图和平面嵌入的概念：
把一个图G的图示画在平面上，使得任何两边除端点外无公共点，则称此种图G为平面图，上述图示为平面图G的一个平面嵌入

2、图可平面嵌入的充要条件：
图G可平面嵌入的充分必要条件是G可球面嵌入

3、推论：
既然可球面嵌入等价于可平面嵌入，可把多面体套在一个球面上，各边贴近球面，即为一个球面嵌入，则说明所有多面体都可以平面嵌入。

4、平面图的欧拉定理：
首先有一些定义需要先说明：
当平面图G平面嵌入之后，把平面划分成的闭区域称为G的面，其数目用ϕ(G)表示，其中有一个无界面，称之为外面（注意：也是属于闭区域）


如果G是平面图，F(G)={f1, f2,…, fϕ}是它的面集合，fi边界上的边之条数记成d(fi), i=l, 2,…, ϕ。d(fi)称为面fi的次数
d(fi)是沿面fi的边界行一周时，历经的边的条数
桥对它所在的面fi的次数之贡献是2

5、平面图的一些推论：
（1）若G是ν≥3的连通平面图，则ε≤3ν-6
（2）如果平面图G有ω个连通片G1, G2,…, Gω，ε≤3ν-6ω
（3）平面图G的最小顶次数δ≤5

6、极大平面图：
定义：若G是ν≥3的平面图，当u, v∈V(G)，而uv∉E(G)时，G+uv不再是平面图，则称G是极大平面图

判定极大平面图的充要条件：ν≥3的平面图G是极大平面图的充分必要条件是G的平面嵌入的每个面皆三角形

ν≥3的平面图是极大平面图的充分必要条件是ε=3ν-6

G是ν≥4的极大平面图，则δ≥3

7、判定平面图的充要条件：
前提：K₅和K~3, 3~不是平面图
定义：同胚图：把图G的一些边的内点处添加一些新顶得到的图，K₅与K~3, 3~的同胚图也是非平面图
充要条件：G是平面图当且仅当G中不含与K₅和K~3, 3~同胚的子图
也可以这么说：G为平面图的充要条件是G中无可收缩成K₅或K~3, 3~的子图

---

四、匹配理论

1、匹配与许配：
M是图G的边子集，且M中任二边在G中不相邻，则称M是G中的一个匹配；M中的每条边的两个端点称为在M中相配；M中每边的端点称为被M许配；G中每个顶点皆被M许配时，称M为G的一个完备匹配；G中边数最多的匹配称为G的最大匹配。
错排问题总数：b(n)=(n-1)[b(n-1)+b(n-2)]

可增广轨：设M是图G中的一个匹配，G中的一条轨P(u, v)上，u与v未被M许配，但P(u, v)上的边交替地不在M中出现与在M中出现，则称P(u, v)为M的可增广轨

覆盖集：设B⊂V(G)，G的每条边皆与B中的顶相关联，则称B是G的一个覆盖集；若B是G的一个覆盖集，但∀v∈B，B-{v}不再是G的覆盖集，则称B是G的极小覆盖；若B是G的顶数最小的覆盖集，则称B为G的最小覆盖，最小覆盖中顶的数目称为G的覆盖数，记成β(G)

2、匹配定理：
（1）（Berge）M是图G中的一个最大匹配当且仅当G中无M的可增广轨
（2）（Hall）设G是二分图，顶集的二分图划分为X与Y，存在把X中顶皆许配的匹配的充要条件是∀S⊆X，|N(S)|≥|S|，其中N(S)是S中每个顶的邻顶组成的所谓S的邻集（推论：易得k（k>0）次正则2分图有完备匹配）
（3）（Konig）若G是二分图，则其最大匹配的边数为β(G)
（4）（Tutte）图G有完备匹配当且仅当∀S⊂V(G)，o(G-S)≤|S|，其中o(G-S)是G-S中奇数个顶的连通片的个数

==> 无桥三次正则图有完备匹配

3、二分图匹配算法：
（1）求最大匹配——匈牙利算法：
核心：不断在图中寻找可增广轨
（2）求最佳匹配——KM算法：
引入定义“正常顶标”：
对Kn, n 的每顶u 给一个顶标l(v) ，∀x∈X, y∈Y，s.t. l(x) + l(y)≥w(xy)
定理：设 K~n, n~ =G是具有正常顶标l 的加权图，取G的边子集El={xy | xy∈E(G), l(x)+l(y)=w(xy)}。令Gl是以El 为边集的G的生成子图，如果Gl有完备匹配M，则M即为G的最佳匹配

4、图的因子分解：
对于给定的图G，把它分解成若干两两无公共边的生成子图G1, G2,…, Gn，且预先要求Gi具有某种性质，即V(Gi)=V(G)，它们的并集=E(G)，E(Gi)⋂E(Gj)=∅，并且要求Gi有性质Pi。称Gi为G的因子，从G求出Gi的过程称为G的因子分解。1个因子是m次正则图时，则称此因子是图G的m因子；若G的因子全是m次正则图时，则称G是可以m因子分解的

定理：
K_2n是可以1因子分解的
K_2n+1存在每个因子皆生成圈的2因子分解，共计n个生成圈

---

五、着色定理

1、图的边着色
（1）定义：
把单图G的边集划分成m个非空子集，即E(G)=子集之并 , Ei∩Ej=∅, i≠j; Ei≠∅, i, j=1, 2,…, m，把Ei中的边用第i种颜色上色，则称对G的边进行了一个m边着色，记成C=(E1, E2,…, Em)。若每个Ei(i=1, 2,…, m)皆G的一个匹配，则称C是G的m边正常着色；当G可以m边正常着色而不能m-1边正常着色时，称m为G的边色数，记之为χ′(G)=m

（2）引理：
（1）设G是连通图，不是奇圈，则存在一种二边着色，使所用的两种颜色在每个次数不小于2的顶所关联的边中出现。
（2）设C=(E1, E2,…, Ek)是G的一个最佳k边着色，如果有一个顶v₀，又存在两种颜色i与j，使得i色在v₀顶关联的边中不出现，而j色在v₀关联的边中至少出现两次，则由Ei⋃Ej导出的子图中含v0的连通片是一个奇圈

（3）定理：
（1）二分图的边色数等于图顶的最大次数
（2）若G是单图，则χ′(G)∈{Δ, Δ+1}
满足χ′(G)=Δ的图为第一类图，否则为第二类

2、图的顶着色：
如果使用n种颜色把图G的每顶皆分配一种颜色，且使得邻顶异色，则称此为对G的顶的正常n着色。图G的顶的正常着色中所需颜色数的最小值称为G的顶色数，简称色数，记之为χ(G)，色数为k的图称为k色图

• G是有边二分图的充要条件是χ(G)=2
• G是无边图当且仅当χ(G)=1
• G是完全图当且仅当χ(G)=|V(G)|
• χ(G)≤Δ(G)+1

设G是平面图，G′是G的平面嵌入，造一个图G*，使得G′的面集合F(G′)是G* 的顶集，当且仅当fi, fi∈F(G′ ) 有公共边时，fi与fj相应的G中的二顶相邻。称G 为G的对偶图。χ(G*)称为图G的面色数

4CC问题：任何平面图的面色数不大于4。由于G*也是平面图，所以4CC也可以转化成：χ(平面图)≤4

3、k顶规范着色：

如果G是可以k顶正常着色的，则G存在k顶规范着色。

4、独立集：
设I⊆V(G)，∀u, v∈I，u与v不相邻，则称I是图G的一个独立集；如果I是独立集，而∀u∈V(G)-I，I⋃{u}不是G的独立集，则称I是G的一个极大独立集；G中顶数最多的独立集称为G的最大独立集，G的最大独立集顶的个数叫做G的独立数，记之为α(G)。在图的正常顶着色中，同色顶组成G的一个独立集

独立集与覆盖集的关系：
I为G的独立集⇔V(G)-I是G的覆盖集
I是G的极大独立集⇔V(G)-I是G的极小覆盖集
α(G)+β(G)=|V(G)|

5、支配集：
V1⊆V(G)，∀v∈V(G)，则v∈V1，不然v与V1内一顶相邻，则称V1为图G的一个支配集。如果V1是图G的一个支配集，但V1的任何真子集不再是G的支配集，则称V1为G的极小支配集。顶数最少的支配集叫做最小支配集，其顶数记成γ(G)， γ(G)称为图G的支配数
任何图G的极大独立集必为G的极小支配集

6、Ramsey数：
（1）定义：
对于2维Ramsey数r(k, l)，上述定义可以转述成下述等价的形式：任给自然数k, l∈N，r(k, l)是满足下列条件的最小的自然数：在r(k, l)个顶的任意图G中，含有k个顶的完全子图或者l个顶的独立集
（2）定理：
k与l是不小于2的自然数，则r(k, l)≤r(k, l-1)+r(k-1, l)，若r(k, l-1)与r(k-1, l)皆为偶数，则上式中的等号不成立

---

六、欧拉图和哈密顿图

1、欧拉图
（1）定义：
欧拉行迹：图G中包含一切边的行迹L

欧拉回路：L是闭行迹，所以欧拉行迹不一定是欧拉回路，但欧拉回路必定是欧拉行迹

欧拉图：存在欧拉回路的图，说白了，就是“一笔画”

（2）判断欧拉图的充要定理：
对于连通图：
（1）G是欧拉图充要条件是任意顶次数为偶数
（2）G是欧拉图充要条件是G可表示成无公共边的圈之并

（3）判定欧拉行迹的充要定理：
连通图中有欧拉行迹当且仅当图中至多两个奇次顶

（4）求欧拉回路的FE算法：
(1)任取v₀∈V(G)，令W₀=v₀
(2)设行迹W_i=v₀v₁v₂…v_i已选定，则从E(G)-E(W)中选一条边e_i+1，使得e_i+1与v_i相关联，且非必要时，e_i+1不要选G-E(W)的桥
(3)反复执行(2)，直至每边e∈E(G)皆入选为止

这个算法核心说白了就是：非必要时，不要通过未用过的边的导出子图的桥

（5）定理：
若G是欧拉图，FE算法终止时得到的W是欧拉回路

（6）中国邮递员问题：
这个问题的实际模型是：一位邮递员从邮局选好邮件去投递，然后返回邮局，他必须经过由他负责投递的每条街道至少一次，为这位邮递员设计一条投递线路，使其耗时最少

中国邮路问题的图论模型是：任给定一个图G，对E_G加权，即对每个e∈E_G，任意指定一个非负实数w_e，求G的一个含有一切边的回路W，使得W的总权Σ_e∈W w_e=min

（7）邮递员问题解法：
(1) 图中奇次顶集为V0={v1,v2,v3,v4}

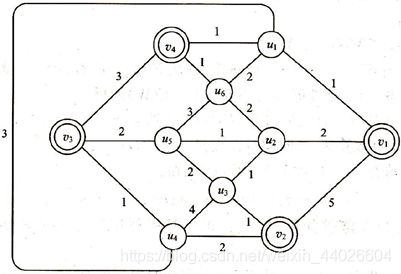
(2) 在V₀中，每对顶的距离为：d(v1, v2)=4, d(v1, v3)=5, d(v1, v4)=2, d(v2, v3)=3, d(v2, v4)=5, d(v3, v4)=3
(3) 构作完全加权图K₄，V(K₄)={v1, v2, v3, v4}，边权w(v_iv_j)=d(v_i, v_j)

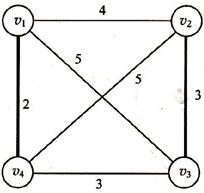
(4) 求(3)中K4的总权最小的完备匹配M={v1v4, v2v3}
(5) 在G中求最短轨P(v1, v4)=v₁u₁v₄，P(v2, v3)= v₂u₄v₃
(6) 在G中沿P(v1, v4)与P(v2, v3)把边变成同权“倍边”

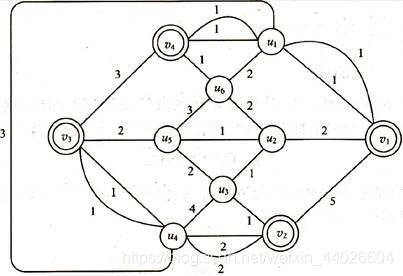
(7) 在Euler图上用FE算法求得一条Euler回路

2、哈密顿图
（1）定义：

哈密顿圈：含图的一切顶的圈

哈密顿图：含哈密顿圈的图就叫哈密顿图

哈密顿轨：含图的一切顶的轨

判断一个图是否为哈密顿图在计算机科学中是个难题。
定理：G是Hamilton图的必要条件是任取S⊂V(G)，S≠∅，则ω(G-S)≤|S|，其中ω(.)是连通片个数

定理：**（Ore）**设|V(G)|≥3，G的任一对顶u, v皆有d(u)+d(v)≥|V(G)|-1，则G中有Hamilton轨；若d(u)+d(v)≥|V(G)|，则G是Hamilton图