【CSP考前复习】关于考试时的注意事项

前言

作为一名已经服役4年的老年OI选手，经历过的考试已经是数以百计了。在这么多次考试中，爆零垫底是常有的事，运气好了靠暴力得到好名次的事也经常发生。那么，CSP临近，我想有必要好好整理一下这些问题和经验。

一、关于暴力

1、为什么要打暴力——得分

这不废话吗考试的时候不打暴力等着爆零吗嘤嘤嘤
首先，我们要明确打暴力是一件非常正确且有用的事：
第一，如果最后想不出正解，暴力的分数拿到手一般也能获得不低的成绩；
第二，出题人有时会把正解的思路放在暴力分里，比如某些DP和数据结构，往往是先引导你打出暴力，然后进一步优化得到正解；
第三，就算真的打出了正解，暴力也是用来对拍的一个好方法，可以让你的正确性得到保证。

当然，有时候出题人想要故意提升题目难度，就会把部分分给的少，甚至可能用部分分来误导思想，不过这种情况一般占少数，在CSP的正规比赛中部分分都是用来提示正解的，只是分明显与否。

2、暴力该怎么打——审题

暴力分往往是在运行时间/空间不够优秀，或者在线/离线这方面有限制时得分的好手段。一般来说，通过观察数据范围可以得到相对应的算法复杂度，这一定程度上有助于考虑暴力和正解。

举个例子，我认为部分分给的最好的——天天爱跑步。我之所以认为这道题的部分分最好，一是因为它具备上面提到的提示效果，你只要打完所有的暴力，再加上思考和码力，就能得到正解；二来，即使你想不出正解，部分分之间的层次性也很强，完全可以根据自己的能力得到对应的分数。

这是部分分的分布：

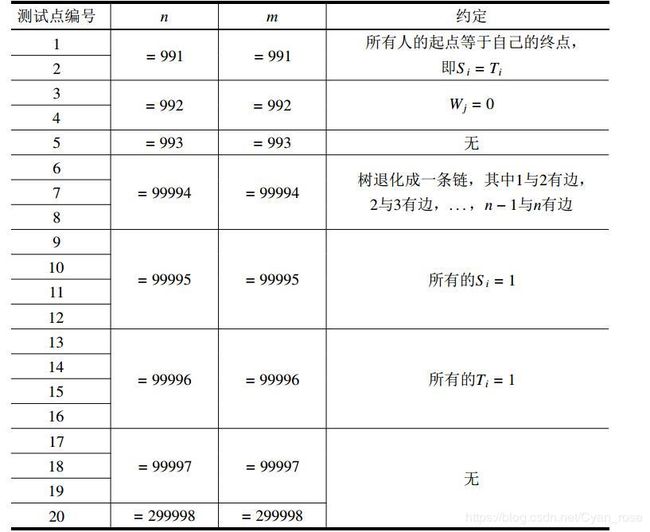
假设我们之前不认识这道题，重新来分析一遍：

1、测试点1~5明显送分，只要读懂题就能想到暴力模拟

2、测试点6~8因为数据范围扩大了，之前的算法不能再用，我们换个思路，考虑每个观察员对什么样的经过路线有贡献，于是思路往差分上走，再通过一些思考可以推出产生贡献的式子

3、测试点9~16举出两种特殊情况，结合6.7.8的差分，再加上一定的模拟，可以得到树上差分的程序。

4、考虑到将链拆为上行和下行两段，发现可以用部分分的解法来分步解决，再加上码力和实现，就可以得到满分程序。

综合上文以及我的经验来看，分析暴力得分以及从暴力到正解一般有以下思路：

1、看数据范围：

常见的有这些：
$n<=10$ 阶乘级算法：枚举全排列
$n<=20$ 指数级算法：暴力搜索，依次枚举，状压DP，多维DP
$n<=500$ N^3 ：DP，搜索剪枝，Floyd，网络流
$n<=2000$ N^2 ：DP，循环迭代，递归处理
$n<=100000$ Nlog^2N~Nsqrt(N)：二分+数据结构，树套树，分块，CDQ，二维树状数组
$n<=500000$ NlogN：线段树，平衡树，DP优化，莫名其妙的贪心
$n<=1000000$ NlogN~N：奇怪的贪心，结论，数学题，树状数组，时限开大了的线段树，最短路，最小生成树，快速幂等（这个档最多
$n<=10000000$ 矩阵快速幂
再往上一般就不是CSP会考的东西了。

2、转化题意

许多的题目其实本质上考察的东西是一样的，只不过由于题面的加工，我们往往不能辨识出这是哪一类问题。这时候就要进行模型转化，将所求的问题分成几个子问题分别求解，或者是转化为一类我们学过的问题。有的题像是DP，但是实际上可能是个结论题或者数学题；有的题看上去是图论，其实可以做出生成树然后转化为树上问题。这一步比较靠个人能力以及做题经验，这里不多阐述。

3、正难则反

如果推DP式子已经到了绞尽脑汁的地步却还是不能过掉全部数据，抑或是在试图优化一个log时无从下手，这时候就要逆向思考。一方面，可以考虑利用当前得到的有用结论，从另一个方面来解决问题；另一方面，如果直接求出满足条件的答案不好实现，我们可以考虑算出不合法的答案，或者是通过二分来转化为检验答案，这样往往能够降低代码难度和思维难度。

4、打表与搜索

这两个算是暴力中最暴力的，但是很多时候打表可以得出很多结论，有时候就能过掉结论题，或者是通过决策单调性优化DP，总之用处很多。读不懂题，可以打表理解；优化不了，可以打表找出规律。而如果搜索得当，像去年NOIP的D2T2，打出正解也不是难事。因此，无论掌握了多么高级的算法，最为基础的这些仍能起到很大的作用。

二、关于查错

在考场上想要拿到高分，光有想法是不够的，还要有足够的实现能力和调试能力。多少人想出了正解，却最后挂在细节上，结果最后还不如暴力分高……

如果想要锻炼实现能力，我推荐去做下猪国杀这样的模拟题；如果想要锻炼调试能力，建议多去做做大杂烩类型的数据结构题，比如树链剖分+换根，LCT+最小生成树+Tarjan，吉司机线段树大全等等……

当然，并不是说做的多就一定能力强，也不是说不做能力就很弱。经过我的总结，做到以下几点，一般可以很快的调试出错误来。

1、认真构思

代码实现的错误很多都是因为在构思时没有考虑到个别特殊情况或者是边界条件，最后反倒会花很多时间来处理这些问题。因此在动手打代码之前，要保证思想已经成熟。当然，也可以一边敲着你已经很熟悉的模板一边思考，但是最核心的部分一定要深思熟虑，考虑到能考虑到的所有情况，尽可能不出差错。比如线段树的pushup和pushdown。既然多数时候都错在这，那么就可以放到最后来实现，争取一次性写对。

2、多写函数

并不是说函数越多越好。在某些重复调用的部分，可以考虑写函数来实现，避免重复的代码造成的代码量大，代码量一大调试难度就会上升。不过，写函数是在你确定这几部分可以用同一个函数实现的前提上，比如猪国杀的抽牌、出牌、死亡判定等。如果牵涉到细节上的不同，而你又拿不准，建议还是展开写，否则后期调试反而会增加难度。

3、对症下药

所谓“症”有多重意思，我们在调试代码时，往往考虑这三点：

①错误的类型。如果是RE或者TLE，多半是在递归函数的地方出了问题，这时候就可以使用return 0大法，判断出是在哪个地方出了问题；如果是WA，那么有可能在某一步之前你的答案都是正确的，此时采用分段输出+人肉检索就可以判断。

②题目的类型。如果是线段树这类的题，多半写挂是在pushup和pushdown上面；如果是模拟、结论题这类，多半是没有考虑到特殊情况和边界条件；而如果是和图有关系，则有可能是在边和点的遍历上有问题。除此之外，在线时是异或lastans还是+lastans，多组数据输入是否数组清零这些都是常见问题。

③自己的问题。打了这么久的代码，大家应该对自己常常犯什么样的错误有印象，比如忘了开longlong，加边加成单向，数组开小，临时变量不初始化等。建议在考前把自己的WA代码拿出来翻一翻，总结一下常见的错误，在考试的时候就要专门针对这些错误进行检查。去年NOIP的考场上我就是因为D2T1数组开小D2T2乘法未及时取模而直接错失一等

下面是我个人总结的一些错误汇总：
不开longlong，vis数组多次调用未清空，忘了把cnt从2开始，数组开小，阶乘的第0位不赋值，一行代码过长导致同一变量写了两次，忘记及时取模，标记下传顺序有误，边界条件考虑失误，二分上下界不对

待补充.jpg