【笔记总结】高中物理——电磁感应中的导轨+单杆/双杆问题
退役蒟蒻写笔记总结ing~
一、单杆问题
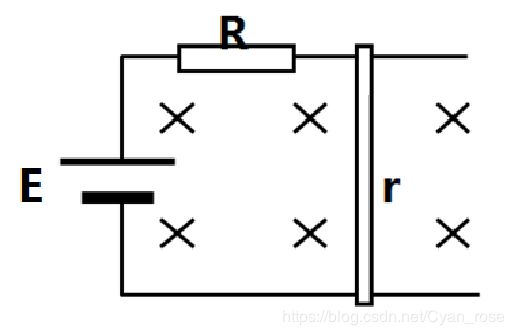
Ⅰ 发电式单杆
①电路特点:
导体棒相当于电源,当速度为 v v v时,电动势 E = B l v E=Blv E=Blv
②安培力特点:
安培力为阻力,并随速度增大而增大(正比)
F B F_B FB= B I l BIl BIl= B B B B l v R + r \frac{Blv}{R+r} R+rBlv = B 2 l 2 v R + r \frac{B^2l^2v}{R+r} R+rB2l2v ∝ v v v
③加速度特点
加速度随速度增大而减小
a a a= F − F B − u m g m \frac{F-F_B-umg}{m} mF−FB−umg= F m \frac{F}{m} mF- B 2 l 2 v m ( R + r ) \frac{B^2l^2v}{m(R+r)} m(R+r)B2l2v
④运动特点:加速度减小的加速运动
⑤最终特征:匀速运动
⑥两个极值
( 1 ) v = 0 (1)v=0 (1)v=0时,有最大加速度: a m a_m am= f r a c F − u m g m frac{F-umg}{m} fracF−umgm
( 2 ) a = 0 (2)a=0 (2)a=0时,有最大速度: a a a= ( F − F B − u m g ) ( R + r ) B 2 l 2 \frac{(F-FB-umg)(R+r)}{B^2l^2} B2l2(F−FB−umg)(R+r)
⑦稳定后的能量转化规律(功率关系)
F v m Fv_m Fvm= ( B l v m ) 2 R + r \frac{(Blv_m)^2}{R+r} R+r(Blvm)2 + u m g v m +umgv_m +umgvm
⑧两个规律
( 1 ) (1) (1)动量定理: F t − B l q − u m g t = m v m − 0 Ft-Blq-umgt=mv_m-0 Ft−Blq−umgt=mvm−0
( 2 ) (2) (2)能量守恒: F s = Q J + u m g S + 1 2 m v m 2 Fs=Q_J+umgS+\frac{1}{2}mv^2_m Fs=QJ+umgS+21mvm2
注意应用: q = n Δ Φ R + r = q=n\frac{ΔΦ}{R+r}= q=nR+rΔΦ= B l ⋅ Δ s R + r \frac{Bl·Δs}{R+r} R+rBl⋅Δs
Ⅱ 电动式单杆
①电路特点
导体为电动边,运动后产生反电动势(等效于电动机)
②安培力的特点
安培力为运动动力,并随速度减小而减小
F B = B I l = B E − E 反 R + r l = B E − B l v R + r L F_B=BIl=B\frac{E-E_反}{R+r}l=B\frac{E-Blv}{R+r}L FB=BIl=BR+rE−E反l=BR+rE−BlvL
③加速度特点
加速度随速度增大而减小
a = F B − u m g m = B E − B l v m ( R + r ) l − u g a=\frac{F_B-umg}{m}=B\frac{E-Blv}{m(R+r)}l-ug a=mFB−umg=Bm(R+r)E−Blvl−ug
④运动特点:a减小的加速运动
⑤最终特征:匀速运动
⑥两个极值
( 1 ) (1) (1)最大加速度: v = 0 v=0 v=0时, E 反 = 0 E_反=0 E反=0,电流、加速度最大
I m = E R + r , F m = B I m , a m = F m − u m g m I_m=\frac{E}{R+r},F_m=BI_m,a_m=\frac{F_m-umg}{m} Im=R+rE,Fm=BIm,am=mFm−umg
( 2 ) (2) (2)最大速度:稳定时,速度最大,电流最小
I I I
v m = E B l − u m g ( R + r ) B 2 l 2 v_m=\frac{E}{Bl}-\frac{umg(R+r)}{B^2l^2} vm=BlE−B2l2umg(R+r)
⑦三个规律
( 1 ) (1) (1)动量定理: B L q − u m g t = m v m − 0 BLq-umgt=mv_m-0 BLq−umgt=mvm−0
( 2 ) (2) (2)能量守恒: q E = Q J + u m g S + 1 2 m v m 2 qE=Q_J+umgS+\frac{1}{2}mv_m^2 qE=QJ+umgS+21mvm2
( 3 ) (3) (3)瞬时加速度: a = F B − u m g m = B ( E − B l v ) m ( R + r ) l − u g a=\frac{F_B-umg}{m}=B\frac{(E-Blv)}{m(R+r)l-ug} a=mFB−umg=Bm(R+r)l−ug(E−Blv)
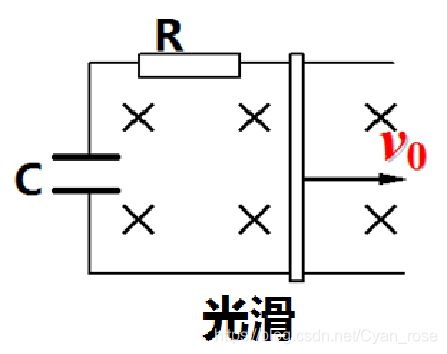
Ⅲ 电容放电单杆
①电路特点
电容器放电,相当于电源;导体棒受安培力而运动。
②电流的特点
电容器放电时,导体棒在安培力作用下开始运动,同时产生阻碍放电的反电动势,导致电流减小直到0,此时 U c = B l v U_c=Blv Uc=Blv
③运动特点
a a a减小的加速运动,最终做匀速运动
④最终匀速运动,但电容器带电量不为0
⑤最大速度 v m v_m vm
电容器充电量: Q 0 = C E Q_0=CE Q0=CE
放电结束时电量: Q = C U = C B l l v m Q=CU=CBllv_m Q=CU=CBllvm
电容器放电电量: Δ Q = Q 0 − Q = C ( E − B l v m ) ΔQ=Q_0-Q=C(E-Blv_m) ΔQ=Q0−Q=C(E−Blvm)
对杆用动量定理L: m v m = B I l ⋅ Δ t = B l Δ Q mv_m=BIl·Δt=BlΔQ mvm=BIl⋅Δt=BlΔQ
v m = B l C E m + B 2 l 2 C v_m=\frac{BlCE}{m+B^2l^2C} vm=m+B2l2CBlCE
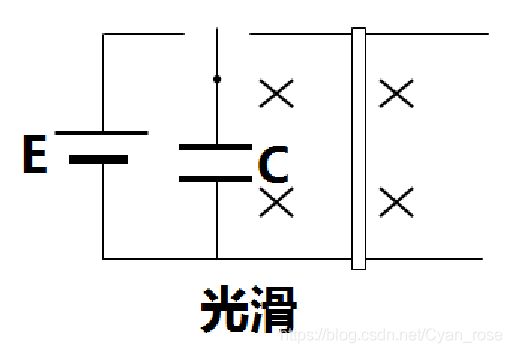
Ⅳ 电容无外力充电式:
①电路特点
导体棒相当于电源,电容器被充电
②电流的特点
导体棒相当于电源; F 安 F_安 F安为阻力,棒减速,E减小
I = B l v − U c R , I I=\frac{Blv-U_c}{R},I I=RBlv−Uc,I逐渐减小
③运动特点
a a a减小的减速运动,最终做匀速运动
④最终匀速运动,但此时电容器带电量不为0
⑤最终速度
电容器充电量: q = C U = C B l v q=CU=CBlv q=CU=CBlv
用动量定理得: m v 0 − m v = B I L ⋅ Δ t = B l q mv_0-mv=BIL·Δt=Blq mv0−mv=BIL⋅Δt=Blq
v = m v 0 m + B 2 l 2 C v=\frac{mv_0}{m+B^2l^2C} v=m+B2l2Cmv0
Ⅴ 电容有外力充电式
①电路特点
导体发电,电容器被充电
②运动性质:匀加速直线运动
证明: I = Δ q Δ t = C ⋅ Δ E Δ t = C B l ⋅ Δ v Δ t = C B l a I=\frac{Δq}{Δt}=\frac{C·ΔE}{Δt}=\frac{CBl·Δv}{Δt}=CBla I=ΔtΔq=ΔtC⋅ΔE=ΔtCBl⋅Δv=CBla
安培力: F A = B I L ⋅ a = F − F A a F_A=BIL·a=\frac{F-F_A}{a} FA=BIL⋅a=aF−FA
a = F m + B 2 l 2 c a=\frac{F}{m+B^2l^2c} a=m+B2l2cF (恒定)
③四个结论
1 、 1、 1、导体棒做初速度为0的匀加速运动
2 、 2、 2、回路中的电流恒定
3 、 3、 3、导体棒受安培力恒定
4 、 4、 4、能量转化:电容器克服安培力——>电容器储存电能
二、双杆问题
Ⅰ 无外力等距双棒
①电路特点
棒2相当于电源;棒1受安培力而加速运动,运动后产生反电动势.
②电流特点
I = B l ( v 2 − v 1 ) R 1 + R 2 I=\frac{Bl(v_2-v_1)}{R_1+R_2} I=R1+R2Bl(v2−v1)
随着棒2的减速、棒1的加速,两帮的相对速度 v 2 − v 1 v_2-v_1 v2−v1变小,回路中电流也变小。
v 1 = 0 v_1=0 v1=0时:电流最大, I m = B l v 0 R 1 + R 2 I_m=\frac{Blv_0}{R_1+R_2} Im=R1+R2Blv0
v 2 = v 1 v_2=v_1 v2=v1时:电流 I I I=0
③两棒的运动情况
安培力: F B = B I l = B 2 l 2 ( v 2 − v 1 ) R 1 + R 2 F_B=BIl=\frac{B^2l^2(v2-v1)}{R1+R2} FB=BIl=R1+R2B2l2(v2−v1)
两棒的相对速度变小,感应电流变小,安培力变小
棒1做加速度变小的加速运动
棒2做加速度变小的减速运动
最终两棒具有相同速度
④两个规律
( 1 ) (1) (1)系统动量守恒:两棒受到的安培力大小相等方向相反,系统合外力为零
因此: m 2 v 0 = ( m 1 + m 2 ) v 共 m_2v_0=(m_1+m_2)v_共 m2v0=(m1+m2)v共
( 2 ) (2) (2)系统能量守恒:系统机械能的减小量=内能增加量
因此: 1 2 m 2 v 0 2 = 1 2 ( m 1 + m 2 ) v 共 2 + Q \frac{1}{2}m_2v_0^2=\frac{1}{2}(m1+m2)v_共^2+Q 21m2v02=21(m1+m2)v共2+Q
Q 1 Q 2 = R 1 R 2 \frac{Q_1}{Q_2}=\frac{R_1}{R_2} Q2Q1=R2R1
⑤变式
改变初速度提供方式(高处滑下),改变磁场方向,两棒都带有初速度
注意:若两棒位于不同磁场中,动量守恒不再成立,但仍有能量守恒
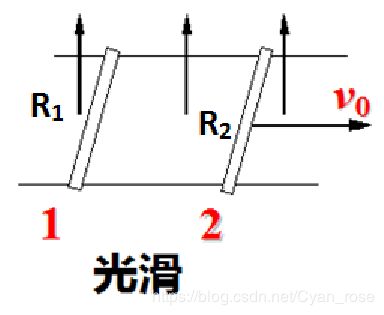
Ⅱ 无外力不等距双杆
1.电路特点
棒1相当于电源;棒2受安培力而起动,运动后产生反电动势
2.电流特点
I = B l 1 v 1 − B l 2 v 2 R 1 + R 2 I=\frac{Bl_1v_1-Bl_2v_2}{R_1+R_2} I=R1+R2Bl1v1−Bl2v2
随着棒1的减速,棒2的加速,回路中电流变小
最终当 B l 1 v 1 = B l 2 v 2 Bl_1v_1=Bl_2v_2 Bl1v1=Bl2v2时,电流为0,两棒都做匀速运动
3.两帮的运动情况
棒1做加速度减小的减速运动,最终匀速;
棒2做加速度减小的加速运动,最终匀速;
4.最终特征
B l 1 v 1 = B l 2 v 2 Bl_1v_1=Bl_2v_2 Bl1v1=Bl2v2,回路中电流为零
5.系统动量不守恒——两棒合外力不为0
6.两杆最终速度
取向右为正,由动量定理得
对棒1有: − B I L 1 t = m 1 v 1 − m 2 v 2 -BIL_1t=m_1v_1-m_2v_2 −BIL1t=m1v1−m2v2 ①
对棒2有: B I L 2 t = m 2 v 2 BIL_2t=m_2v_2 BIL2t=m2v2 ②
①/②得: L 1 L 2 = m 1 ( v 0 − v ) m 2 v 2 \frac{L_1}{L_2}=\frac{m_1(v_0-v)}{m_2v_2} L2L1=m2v2m1(v0−v) ③
匀速时无电流,总电动势为0,即 B L v 1 = B L v 2 BLv_1=BLv_2 BLv1=BLv2 ④
由③④联立得:
v 1 = m 1 l 2 2 m 1 l 2 2 + m 2 v 2 2 v 0 v_1=\frac{m_1l_2^2}{m_1l_2^2+m_2v_2^2}v0 v1=m1l22+m2v22m1l22v0
v 2 = m 1 L 1 L 2 m 2 L 2 2 + m 2 L 1 2 v 0 v_2=\frac{m_1L_1L_2}{m_2L_2^2+m_2L_1^2}v0 v2=m2L22+m2L12m1L1L2v0