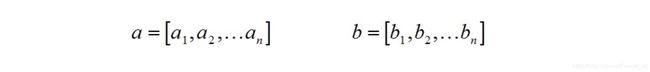OpenGL之3D数学的向量和矩阵

向量

基本概念

• 既有大小又有方向的量称之为向量，与之相对应的是标量，标量是只有大小没有方向的量；
• 在3D笛卡尔坐标系：基本上，一个顶点就是XYZ 坐标空间上的一个位置，而在空间中给定的⼀个位置恰恰是由⼀个单独的 XYZ 定义的，而这样的 XYZ 就是向量;
• 长度为0的向量称之为零向量，零向量与所有向量平行；
• 模为1的向量称之为单位向量，单位向量并不是唯一的，每个向量单位化以后都是单位向量；
• 空间向量长度(向量的模)计算公式：

• math3d库，有2个数据类型，能够表示一个三维或者四维向量：
  M3DVector3f可以表示⼀个三维向量(x,y,z)， M3DVector4f则可以表示⼀个四维向量(x,y,z,w)；（在典型情况下，w坐标设为1.0。x,y,z值通过除以w，来进行缩放。而除以1.0则本质上不改变x,y,z值 ）

   // 三维向量/四维向量的声明
   typedef float M3DVector3f[3]; 
   typedef float M3DVector4f[4];
   // 声明⼀个三维向量 M3DVector3f:类型 vVector:变量名 
   M3DVector3f vVector;
   // 声明一个四维向量并初始化⼀个四维向量 
   M3DVector4f vVertex = {0,0,1,1};
   // 声明一个三分量顶点数组，例如生成⼀个三角形 
   M3DVector3f vVerts[] = {
                        -0.5f,0.0f,0.0f, 
                        0.5f,0.0f,0.0f, 
                        0.0f,0.5f,0.0f};

运算

一、向量的数乘

• 向量的数乘表示向量跟一个实数相乘的乘积，结果还是一个向量。 比如实数a跟一个向量V=(Vx, Vy)相乘，结果为aV=(aVx, aVy)；
• 在坐标轴中，如果一个物体的位置为A(3, 3, 3)，如果将其位置乘以2再赋值给这个物体，那么A的位置就会变成A’(6,6,6)。也就是说，将这个物体的位置从A点移动到了A’点.

二、向量的加法

• 两个向量相加以后的结果还是一个向量，新向量的各个分量的值等于两个向量的对应分量的加值。计算公式为A + B = (A1 + B1, A2 + B2 … , An + Bn)（例如两个二维向量相加，向量C等于向量A(3, 4)加向量B(5, 6)，即：C = A + B = (3+5, 4+6)）；
• 遵循“平行四边形法则”和“三角形法则”；
  

三、向量的减法

• 两个向量相减所得还是一个向量，这个向量的各个分量的值为旧向量的各个分量的差值。公式为：A - B = (A1 + B1, A2 + B2 … , An + Bn)。（例如两个二维向量相加，向量C等于向量A(3, 4)加向量B(5, 6)，即：C = A - B = (3-5, 4-6)）
• 遵循“三角形法则”：减法的所得的最终向量，其方向是由减数向量的终点指向被减数向量的终点。
  

四、向量的点乘（dot product）

• 向量的点积表示为A · B = A1B1 + A1B1 + … + AnBn；
• 几何意义：点乘表示了两个向量的接近程度，即夹角越小，两个向量越靠近，在等于0的时候平行，等于1的时候垂直。因此向量的点乘在游戏中经常用来判断两个向量的接近程度。比如两个移动的物体是否会撞上，需要不需要避开之类的AI计算。同时，已知两个向量，可以计算两个向量的夹角。从而进行旋转操作等
  A·B > 0，则夹角在[0, 90)；
  A·B = 0，则夹角等于 90，两个向量垂直
  A·B < 0，则夹角在(90,180)
• 点乘只能在2个向量之间进行；
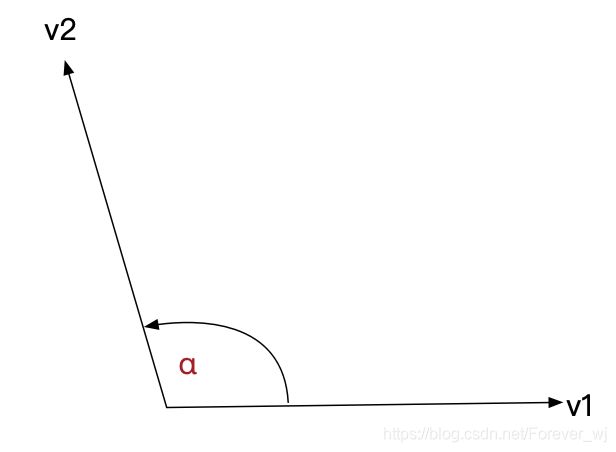
• 2个(三维向量)单元向量之间进行点乘运算将得到⼀个标量(不是三维向量，是⼀个标量)，它表示两个向量之间的夹⻆；
  
• 性质：
  A·B = B·A 点乘满足交换律；
  A·(B + C) = A·B + A·C 点乘满足分配律；
  (aA)·B = a(A·B) 一个实数不影响两个向量的点乘
• math3d 库中提供了关于点乘的API：

// m3dDotProduct3 函数获得2个向量之间的点乘结果，即余弦值cosα
float m3dDotProduct3(const M3DVector3f u,const M3DVector3f v);

// m3dGetAngleBetweenVector3 即可获取2个向量之间夹角的弧度值 α = arccos余弦
float m3dGetAngleBetweenVector3(const M3DVector3f u,const M3DVector3f v);

五、向量的叉乘（cross product）

• 两个叉乘所得出的新向量，垂直与这两个向量，并穿过这两个向量的交叉点。新向量的方向则取决于使用的坐标系，Unity使用的是左手坐标系，OpenGL使用的是右手坐标系。左手坐标系中，左手掌心向外，食指向上，中指向前，大拇指的方向就是x轴，食指指向的是y轴，中指指向的是z轴，将两个向量对准坐标轴，剩余的一个方向就是新向量的方向。
  
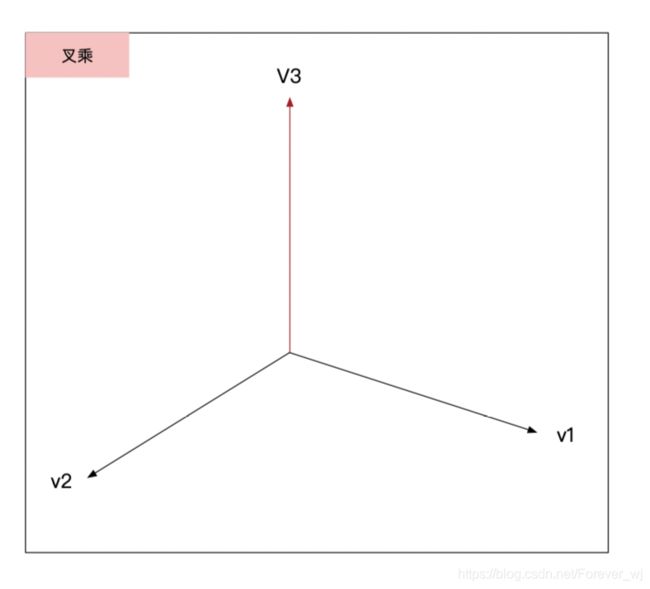
• 叉乘的模：|A X B| = |A||B|sinα，其中α是两个向量的夹角；
• math3d 库中提供了关于叉乘的API

    // m3dCrossProduct3 函数获得2个向量之间的叉乘结果得到⼀个新的向量
    void m3dCrossProduct3(M3DVector3f result,const M3DVector3f  u ,const
    M3DVector3f v);

矩阵（Matrix）

概念

• 在其他编程标准中, 许多矩阵库定义一个矩阵时，使用⼆维数组；OpenGL的约定里，更多倾向使用一维数组；
• 矩阵声明

    // 三维矩阵/四维矩阵的声明
    typedef float M3DMatrix33f[9];
    typedef float M3DMatrix44f[16];

• OpenGL 使⽤的是 Column-Major(以列为主)矩阵排序的约定；⾏优先矩阵（左）和列优先矩阵（右）如下图所示：
  

• ⾏优先矩阵与列优先矩阵互为转置矩阵；

• 矩阵的这16个值表示空间中⼀个特定的位置； 这4列中，每⼀列都是有4个元素组成的向量;（第一列：X轴方向，第二列：Y轴方向，第三列：Z轴方向，第四列：交换位置）；

• 如果将⼀个对象所有的顶点向量乘以矩阵，就能让整个对象变换到空间中给定的位置和⽅向；

• 列向量进行了特别的标注：矩阵的最后⼀行都为0，只有最后⼀个元素为1。

单元矩阵

• 主对角线上数据都是1，其余元素都是0，即为单元矩阵。其初始化方式有：

// 单元矩阵初始化⽅式1
GLFloat m[] = {
           1,0,0,0,  // X Column
           0,1,0,0,  // Y Column
           0,0,1,0,  // Z Column
           0,0,0,1}; // Translation
// 单元矩阵初始化方式2
M3DMatrix44f m = {
           1,0,0,0, // X Column
           0,1,0,0, // Y Column
           0,0,1,0, // Z Column
           0,0,0,1};// Translation
// 单元矩阵初始化⽅式3
void m3dLoadIdentity44f(M3DMatrix44f m);

• 将⼀个向量✖ 单元矩阵，就相当于⼀个向量✖1， 不会发⽣任何改变；

• 在线性代数中：
  变换后顶点向量 = V_local * M_model * M_view * M_pro
  变换后顶点向量 = 顶点 ✖ 模型矩阵 ✖ 观察矩阵 ✖ 投影矩阵
  

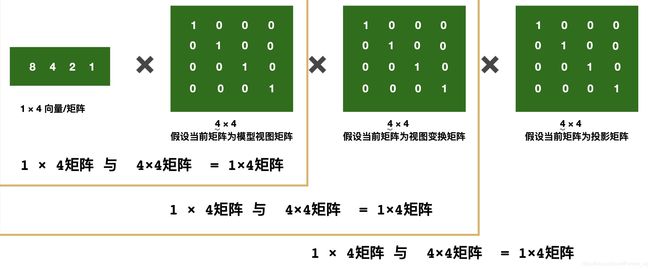
• 在OpenGL 的维度，如下列公式:
  变换顶点向量 = M_pro * M_view * M_model * V_local
  变换顶点向量 = 投影矩阵 ✖ 视图变换矩阵 ✖ 模型矩阵 ✖ 顶点

• 矩阵左乘的代码如下：
  从栈顶获取栈顶矩阵复制到 mTemp；将栈顶矩阵 mTemp 左乘 mMatrix；将结果放回栈顶空间⾥；

        inline void MultMatrix(const M3DMatrix44f mMatrix) {
            // 矩阵左乘 
			M3DMatrix44f mTemp;
			m3dCopyMatrix44(mTemp, pStack[stackPointer]);
			m3dMatrixMultiply44(pStack[stackPointer], mTemp, mMatrix);
			}
            
        inline void MultMatrix(GLFrame& frame) {
            M3DMatrix44f m;
            frame.GetMatrix(m);
            MultMatrix(m);
            }
            

• ChangeSize函数中，得到投影矩阵，将投影矩阵压入投影矩阵堆栈栈顶，并与模型视图矩阵栈顶相乘，将结果覆盖栈顶，即 投影矩阵 * 单元矩阵 = 投影矩阵；
  RenderScene函数中，将栈顶矩阵copy一份，然后将观察者矩阵与模型视图矩阵堆栈栈顶相乘，其结果覆盖栈顶矩阵，即投影矩阵 * 视图矩阵 = 视图投影矩阵；
  得到模型矩阵，将模型矩阵与栈顶矩阵相乘，其结果覆盖栈顶矩阵，即栈顶 = 模型视图投影矩阵；

    // 投影矩阵 projectionMatrix
    modelViewMatrix.PushMatrix();
    M3DMatrix44f pm;
    projectionMatrix.GetMatrix(pm);
    modelViewMatrix.MultMatrix(pm);
    
    // 观察者矩阵 viewMatrix
    modelViewMatrix.PushMatrix();
    M3DMatrix44f mCamera;
    cameraFrame.GetCameraMatrix(mCamera);
    modelViewMatrix.MultMatrix(mCamera);
    
    // 模型变换矩阵 modelMatrix
    M3DMatrix44f mObjectFrame;
    viewFrame.GetCameraMatrix(mObjectFrame);
    modelViewMatrix.MultMatrix(mObjectFrame);
    

矩阵的运算

矩阵的点乘

• A*B是以数学运算中矩阵相乘的方式实现的，即Mat矩阵A和B被当做纯粹的矩阵做乘法运算，这就要求A的列数等于B的行数时，才能定义两个矩阵相乘。如A是m×n矩阵，B是n×p矩阵，它们的乘积AB是一个m×p矩阵。
  
• C中第i行第j列所在元素C(i,j)等于A中第i行所有元素跟B中第j列所有元素一一对应的乘积之和。对于A、B都是2行2列矩阵的情况：
  

矩阵的dot（A.dot(B)）

• A.dot(B)操作相当于数学向量运算中的点乘，也叫向量的内积、数量积；

• 对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量；

• 对于向量a和向量b：
  
  a和b的点积公式为：
  
  要求向量a和向量b的行列数相同。

• Mat矩阵的dot方法扩展了一维向量的点乘操作，把整个Mat矩阵扩展成一个行（列）向量，之后执行向量的点乘运算，仍然要求参与dot运算的两个Mat矩阵的行列数完全一致；

• dot方法声明中显示返回值是double，所以A.dot(B)结果是一个double类型数据，不是Mat矩阵，不能把A.dot(B)结果赋值给Mat矩阵。

• dot操作不对参与运算的矩阵A、B的数据类型做要求，CV_8UC1、CV_32FC1等，可以是任何Opencv定义的类型；

• 若参与dot运算的两个Mat矩阵是多通道的，则计算结果是所有通道单独计算各自.dot之后，再累计的和，结果仍是一个double类型数据。