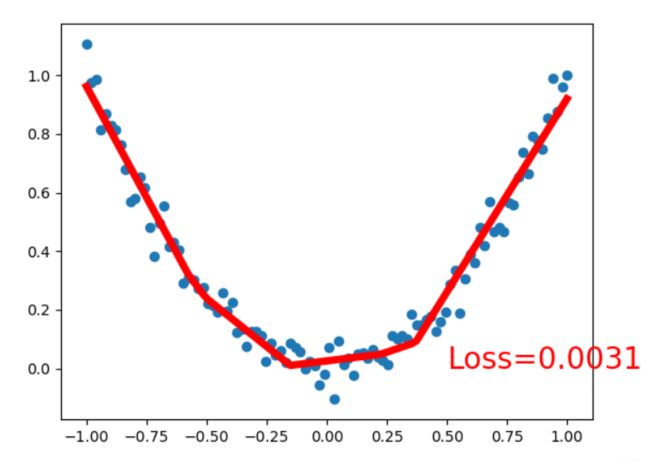
PyTorch入门(一)PyTorch基础、线性回归、Logistic回归和简单的神经网络
PyTorch入门
- PyTorch基础
- forward 的使用与解释
- 反向传播
- 批训练数据
- 常用优化器
- 模型保存和加载
- 预训练模型的使用
- GPU加速
- 线性模型
- 单变量线性回归
- 分类问题
- 二元分类问题
- 多分类问题
PyTorch基础
forward 的使用与解释
类的 __call __() 函数
当把类当做函数调用进行使用时,会自动调用该类的 __call __() 函数。
例子如下:
class A():
def __call__(self, param):
print('i can called like a function')
print('传入参数的类型是:{} 值为: {}'.format(type(param), param))
res = self.forward(param)
return res
def forward(self, input_):
print('forward 函数被调用了')
print('in forward, 传入参数类型是:{} 值为: {}'.format( type(input_), input_))
return input_
a = A()
input_param = a('i')
print("对象a传入的参数是:", input_param)
输出
i can called like a function
传入参数的类型是:<class ‘str’> 值为: i
forward 函数被调用了
in forward, 传入参数类型是:<class ‘str’> 值为: i
对象a传入的参数是: i
forward
网络模型类一般会继承nn.Module父类,nn.Module父类中定义了__call__() 函数。
因此,在模型训练时,不需要使用forward,只要在实例化一个对象中传入对应的参数就可以自动调用 forward 函数
反向传播
- 标量的反向传播
y.backward()
不需要传入参数,相当于 y.backward(torch.Tensor([1]))
import torch
x = [[1,2],[3,4],[5,6]]
x = torch.Tensor(x)
x.requires_grad = True
y = 2*x*x
y = y.mean() #此时y是一个标量,也就是0维张量
y.backward()
print(x.grad)
输出
tensor([[0.6667, 1.3333],
[2.0000, 2.6667],
[3.3333, 4.0000]])
- 矩阵/向量的反向传播
y.backward ( 与矩阵 y 同维的Tensor )
import torch
x = [[1,2],[3,4],[5,6]]
x = torch.Tensor(x)
x.requires_grad = True
y = 2*x*x
y.backward(torch.ones(3,2))
print(x.grad)
输出
tensor([[ 4., 8.],
[12., 16.],
[20., 24.]])
批训练数据
Mini-batch Training
批训练数据:每次训练神经网络时,不使用全部的训练集,只是用一小批数据
主要使用torch.utils.data.DataLoader函数进行分批次
loader = data.DataLoader(
dataset=dataset,
batch_size=BATCH_SIZE,
shuffle=True #每次分批次时重新打乱原来数据的顺序
)
import torch
import torch.utils.data as data #用于批训练数据
BATCH_SIZE = 5
x= torch.linspace(1,10,10)
y = torch.linspace(1,10,10)
#自定义数据集
dataset = data.TensorDataset(x,y)
#使用DataLoader函数进行数据分批
loader = data.DataLoader(
dataset=dataset,
batch_size=BATCH_SIZE,
shuffle=True
)
for epoch in range(3):
for i,(data_x,data_y) in enumerate(loader):
#training
print('Epoch: ',epoch,'|第 %s 批次'%(i),'|data_x: ',data_x.numpy(),'|data_y: ',data_y.numpy())
批训练数据的输出结果:
Epoch: 0 |第 0 批次 |data_x: [3. 1. 8. 5. 4.] |data_y: [3. 1. 8. 5. 4.]
Epoch: 0 |第 1 批次 |data_x: [ 2. 10. 7. 9. 6.] |data_y: [ 2. 10. 7. 9. 6.]
Epoch: 1 |第 0 批次 |data_x: [ 4. 2. 5. 3. 10.] |data_y: [ 4. 2. 5. 3. 10.]
Epoch: 1 |第 1 批次 |data_x: [6. 1. 8. 9. 7.] |data_y: [6. 1. 8. 9. 7.]
Epoch: 2 |第 0 批次 |data_x: [3. 9. 6. 5. 1.] |data_y: [3. 9. 6. 5. 1.]
Epoch: 2 |第 1 批次 |data_x: [ 8. 2. 4. 10. 7.] |data_y: [ 8. 2. 4. 10. 7.]
常用优化器
-
SGD
随机梯度下降
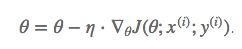
SGD的噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。所以虽然训练速度快,但是准 确度下降,并不是全局最优。虽然包含一定的随机性,但是从期望上来看,它是等于正确的导数的。优点:
损失函数收敛速度比BGD快,每次只需要训练一批次的样本数据缺点
1)SGD 因为更新比较频繁,会造成 cost function 有严重的震荡。
2)SGD容易被困在鞍点处,只取得局部最小值
-
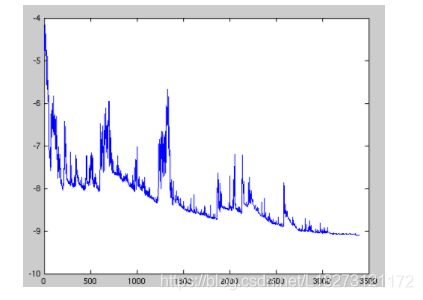
Momentum
动量梯度下降法

超参数设定值: 一般 β \beta β 取值 0.9 左右。优点:Momentum方法可以使得梯度方向不变的维度上更新速度变快,梯度方向改变的维度上更新速度变慢,从而相应地可以加快收敛和减小振荡。
缺点:这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚,如果它能具备一些先知,例如快要上坡时,就知道需要减速了的话,适应性会更好。
-
RMSprop
RMSprop是一种学习率自适应调节的方法,可以解决Adagrad中学习率急剧下降的问题
RMSprop 使用的是指数加权平均,旨在消除梯度下降中的摆动,与Momentum的效果一样,某一维度的导数比较大,则指数加权平均就大,某一维度的导数比较小,则其指数加权平均就小,这样就保证了各维度导数都在一个量级,进而减少了摆动。允许使用一个更大的学习率η
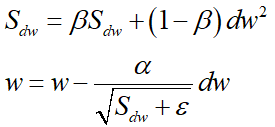
超参数设定值: 一般 β \beta β 取值 0.9 左右。 -
Adam
Adam方法是RMSprop + Momentum
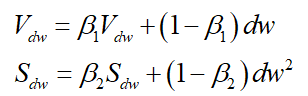
在网络训练的初始阶段时,Vdw和 Sdw 被初始化为 0 向量,那它们就会向 0 偏置,导致移动加权平均的结果和原值偏差较大,所以做了偏差校正,通过计算偏差校正后的 Vdw 和 Sdw 来抵消这些偏差:
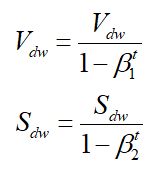
更新权重参数w
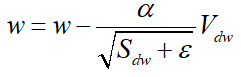
超参数设定值: β1 = 0.9,β2 = 0.999, ε \varepsilon ε=10^-8
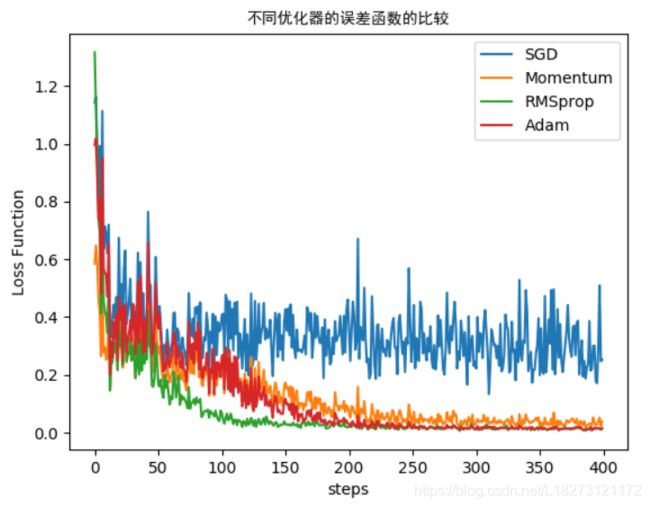
以线性回归模型为例测试优化器SGD、Momentum、RMSprop和Adam的性能
#测试优化器SGD、Momentum、RMSprop和Adam的性能
#以线性回归模型为例
import torch
import torch.nn as nn
import torch.utils.data as data
import torch.nn.functional as F
import matplotlib.pyplot as plt
#hyper parameters
LR = 0.01
EPOCH = 10
BATCH_SIZE = 25
#准备数据
x = torch.unsqueeze(torch.linspace(-1,1,1000),1) #输入数据维度:1000*1
y = 2 * x * x + 0.1 * torch.randn(x.size())
dataset = data.TensorDataset(x,y)
loader = data.DataLoader(
dataset = dataset,
batch_size=BATCH_SIZE,
shuffle=True
)
#构建网络
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
self.hidden = nn.Linear(1,10)
self.outputLayer = nn.Linear(10,1)
def forward(self,x):
x = F.relu(self.hidden(x))
x = self.outputLayer(x)
return x
netSGD = Net()
netMomentum = Net()
netRMSprop = Net()
netAdam = Net()
nets = [netSGD,netMomentum,netRMSprop,netAdam]
#定义损失函数和优化器
criterion = nn.MSELoss()
optim_SGD = torch.optim.SGD(netSGD.parameters(), lr = LR)
optim_Momentum = torch.optim.SGD(netMomentum.parameters(), lr = LR, momentum=0.8)
optim_RMSprop = torch.optim.RMSprop(netRMSprop.parameters(), lr = LR, alpha = 0.9)
optim_Adam = torch.optim.Adam(netAdam.parameters(),lr = LR, betas=(0.9,0.99))
optimizers = [optim_SGD,optim_Momentum,optim_RMSprop,optim_Adam]
losses_his = [[],[],[],[]] #记录不同优化器对应模型的误差
#训练网络
for epoch in range(EPOCH):
for steps,(data_x,data_y) in enumerate(loader):
for net,optimizer,loss_his in zip(nets,optimizers,losses_his):
optimizer.zero_grad()
outputs = net(data_x)
loss = criterion(outputs,data_y)
loss.backward()
optimizer.step()
loss_his.append(loss)
print('Training finished!')
labels = ['SGD','Momentum','RMSprop','Adam']
for i in range(4):
plt.plot(losses_his[i],label=labels[i])
plt.legend(loc = 'best')
plt.title('不同优化器的误差函数的比较',fontproperties = 'simHei')
plt.xlabel('steps')
plt.ylabel('Loss Function')
plt.show()
 ***
***
模型保存和加载
①保存和加载整个模型
#保存模型
torch.save(net, 'net.pkl')
#加载模型
net = torch.load('net.pkl')
②只保存模型中的参数
#保存模型参数
torch.save(net.state_dict(), 'net_parameters.pth')
#加载模型参数
net.load_state_dict(torch.load('net_parameters.pth'))
预训练模型的使用
#微调基础模型预训练
import torch
from torch import nn
from torchvision import models
#使用基础模型和预训练好的参数
pretrained_model = models.resnet18(pretrained = True)
#微调基础模型
#将最后一层全连接层的输出类别改为我们的类别
numclasses = 21
in_features = pretrained_model.fc.in_features
pretrained_model.fc = nn.Linear(in_features,numclasses)
GPU加速
将数据,模型和损失函数放到cuda平台上进行GPU加速
- 数据:images = images.cuda()
- 模型: net = net.cuda()
- 损失函数: criterion = criterion.cuda()
线性模型
单变量线性回归
输入X是100×1的矩阵:只有1个特征,共有100个样本
网络模型共有两层:
- Hidden Layer: 10个隐藏单元
- Output Layer: 1个输出单元
Loss函数:均方误差函数(MSELoss)
优化器:随机梯度下降(SGD)
import torch
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
x = torch.unsqueeze(torch.linspace(-1,1,100),dim = 1)
y = x * x + 0.05 * torch.randn(x.size())
# #绘制散点图
# plt.scatter(x.numpy(),y.numpy())
# plt.show()
#搭建网络
class Net(nn.Module):
def __init__(self,n_features,n_hidden,n_ouputs):
super(Net,self).__init__()
self.hidden = nn.Linear(n_features,n_hidden)
self.fc = nn.Linear(n_hidden,n_ouputs)
def forward(self,x):
x = F.relu(self.hidden(x))
#输出层不用激活函数
x = self.fc(x)
return x
net = Net(1,10,1)
#定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(net.parameters(),lr = 0.05)
plt.ion()
#训练网络
for epoch in range(2000):
#清空优化器的梯度
optimizer.zero_grad()
#计算梯度:计算误差,反向传播
outputs = net(x)
loss = criterion(outputs,y)
loss.backward()
#更新参数
optimizer.step()
if epoch % 5 == 0:
# plot and show learning process
plt.cla()
plt.scatter(x.numpy(), y.numpy())
plt.plot(x.numpy(), outputs.data.numpy(), 'r-', lw=5)
plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
plt.pause(0.1)
plt.ioff()
plt.show()
分类问题
二元分类问题
此次搭建的浅层神经网络只有两个输出单元,可以用于二分类问题
- 网络结构
输入特征数:2个
中间隐藏层:只有1层,每层有10个隐藏单元
输出单元:2个 - Loss函数:交叉熵损失函数(CrossEntropyLoss)
- 优化器:Momentum优化器,梯度累计参数为 0.8
- 在测试集上的准确率
Accuracy of the net on the test set: 99.500 %
#Softmax Regression
import torch
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
import numpy as np
# torch.manual_seed(1) # reproducible
# make fake data
#training set
n_data = torch.ones(100, 2)
x0 = torch.normal(2*n_data, 1) # class0 x data (tensor), shape=(100, 2)
y0 = torch.zeros(100) # class0 y data (tensor), shape=(100, 1)
x1 = torch.normal(-2*n_data, 1) # class1 x data (tensor), shape=(100, 2)
y1 = torch.ones(100) # class1 y data (tensor), shape=(100, 1)
x = torch.cat((x0, x1), 0).type(torch.FloatTensor) # shape (200, 2) FloatTensor = 32-bit floating
y = torch.cat((y0, y1), ).type(torch.LongTensor) # shape (200,) LongTensor = 64-bit integer
#test set
test_x0 = torch.normal(2*n_data, 1) # class0 x data (tensor), shape=(100, 2)
test_y0 = torch.zeros(100) # class0 y data (tensor), shape=(100, 1)
test_x1 = torch.normal(-2*n_data, 1) # class1 x data (tensor), shape=(100, 2)
test_y1 = torch.ones(100) # class1 y data (tensor), shape=(100, 1)
test_x = torch.cat((test_x0, test_x1), 0).type(torch.FloatTensor) # shape (200, 2) FloatTensor = 32-bit floating
test_y = torch.cat((test_y0, test_y1), ).type(torch.LongTensor) # shape (200,) LongTensor = 64-bit integer
# plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
# plt.show()
#搭建网络
class Net(nn.Module):
def __init__(self,n_features,n_units,n_ouputs):
super(Net,self).__init__()
self.fc1 = nn.Linear(n_features,n_units)
self.fc2 = nn.Linear(n_units,n_ouputs)
def forward(self,x):
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
net = Net(2,10,2)
#定义优化器和Loss函数
opitimizer = torch.optim.SGD(net.parameters(),lr = 0.1,momentum = 0.8)
criterion = nn.CrossEntropyLoss()
lossArray = []
#plt.ion()
#训练网络
for epoch in range(100):
#梯度清空
opitimizer.zero_grad()
#计算梯度
outputs = net(x)
loss = criterion(outputs,y)
loss.backward()
#更新参数
opitimizer.step()
lossArray.append(loss)
# if epoch % 2 == 0:
# plt.cla()
# _, predicted = torch.max(outputs,1)
# train_accuracy = (predicted == y).sum().item()/float(y.size(0))*100
# plt.scatter(x.numpy()[:, 0], x.numpy()[:, 1], c=predicted.numpy(), s=100, lw=0, cmap='RdYlGn')
# plt.text(1.5, -4, 'Accuracy=%.3f %%' % train_accuracy, fontdict={'size': 20, 'color': 'red'})
# plt.pause(0.01)
# plt.ioff()
# plt.show()
#测试网络
outputs = net(test_x)
_, predicted = torch.max(outputs,1)
test_accuracy = (predicted == test_y).sum().item()/float(test_y.size(0))
print('Accuracy of the net on the test set: %.3f %%'%(test_accuracy*100))
plt.subplot(2,1,1)
plt.scatter(x.numpy()[:, 0], x.numpy()[:, 1], c=y.numpy(), s=100, lw=0, cmap='RdYlGn')
plt.subplot(2,1,2)
plt.plot(np.linspace(1,100,100),lossArray)
plt.title('Loss Function Curve')
plt.xlabel('iteration')
plt.ylabel('Loss Function')
plt.show()
输入数据的分布与Loss函数曲线如下图:

多分类问题
搭建一个三层全连接层的神经网络,用于MNIST手写数字分类
-
MNIST数据集:
- 60000张训练图片,10000张测试图片
- 数据集按照数字 0-9 分为10类
- 图片格式:(1,28,28) 灰度图像,每张大小为 28 × \times × 28
-
网络结构:
Net(
(fc1): Sequential(
(0): Linear(in_features=784, out_features=400, bias=True)
(1): BatchNorm1d(400, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU()
)
(fc2): Sequential(
(0): Linear(in_features=400, out_features=100, bias=True)
(1): BatchNorm1d(100, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU()
)
(fc3): Linear(in_features=100, out_features=10, bias=True)
)
- 准确率
-
Train set: Accuracy: 98.64 %
-
Test set: Accuracy: 97.75 %
由三层全连接层构成的神经网络在MNIST数据集的分类准确率可以达到 97.75%
代码如下:
#全连接层神经网络 --> MNIST 手写数字分类
import torch
import torch.nn as nn
import torch.utils.data as data
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
#set hyper parameters
LR = 0.01
EPOCH = 20
BATCH_SIZE = 60
DOWNLOAD_MNIST = False
# prepare train_set and test_set
transforms = transforms.Compose([transforms.ToTensor(),
transforms.Normalize([0.5],[0.5])])
train_set = torchvision.datasets.MNIST(root='./data/MNIST',
train=True,
transform = transforms,
download=DOWNLOAD_MNIST)
train_loader = data.DataLoader(dataset=train_set,
batch_size=BATCH_SIZE,
shuffle=True)
test_set = torchvision.datasets.MNIST(root='./data/MNIST',
train=False,
transform = transforms,
download=DOWNLOAD_MNIST)
test_loader = data.DataLoader(dataset=test_set,
batch_size=BATCH_SIZE,
shuffle=True)
# build the net
class Net(nn.Module):
def __init__(self,n_features,n_hidden1,n_hidden2,n_outputs):
super(Net, self).__init__()
self.fc1 = nn.Sequential(nn.Linear(n_features,n_hidden1),
nn.BatchNorm1d(n_hidden1),
nn.ReLU())
self.fc2 = nn.Sequential(nn.Linear(n_hidden1,n_hidden2),
nn.BatchNorm1d(n_hidden2),
nn.ReLU())
self.fc3 = nn.Linear(n_hidden2,n_outputs)
def forward(self,x):
x = x.view(x.size(0),-1)
x = self.fc1(x)
x = self.fc2(x)
x = self.fc3(x)
return x
net = Net(28*28,400,100,10)
print('Net的结构:\n',net)
#define Loss Function and optimizer
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=LR, betas=(0.9,0.99))
#train the net
correct_train = 0
total_train = 0
losses_his = []
for epoch in range(EPOCH):
print('Epoch: ',epoch)
for i, (images,labels) in enumerate(train_loader):
#images: Tensor(60,1,28,28)
#labels: Tensor(60)
optimizer.zero_grad()
outputs = net(images)
loss = criterion(outputs,labels)
loss.backward()
optimizer.step()
losses_his.append(loss)
if (i+1) % 50 == 0:
_, predicted = torch.max(outputs,1)
correct_train +=(predicted == labels).sum().item()*50
total_train += labels.size(0)*50
accuracy = (predicted == labels).sum().item()/labels.size(0)
print('Batch: [%d/%d]'%(i+1,60000/BATCH_SIZE),'|Loss: ',loss.item(),'|Accuracy: %.2f %%'%(accuracy*100))
accuracy_train = correct_train/total_train
print('Training Finished !\nTrain set: Accuracy: %.2f %%'%(accuracy_train*100))
torch.save(net.state_dict(),'./model/DNN_3Layers_MNIST.pkl')
print('The model trained is saved successfully!\n')
#test the net
num_correct = 0
total_test = 0
net.eval()
with torch.no_grad():
for (images,labels) in test_loader:
outputs = net(images)
_, predicted = torch.max(outputs,1)
num_correct += (predicted == labels).sum().item()
total_test += labels.size(0)
test_accuracy = num_correct/ total_test*100
print('Test set: Accuracy: %.2f %%'%(test_accuracy))
#visualization
plt.plot(losses_his)
plt.title('Loss Function Curve')
plt.xlabel('iteration')
plt.ylabel('Loss')
plt.show()