算法导论(第三版)-复习15动态规划
15 动态规划
1 课后习题
15.1-1 数学归纳法证明
15.1-2 总长6,(i=4,p=8),(i=3,p=5)
15.1-3 rn =max( pi -c+ rn−i ),i=1..n
15.1-4 纪录每次切割i
15.1-5 顶点:0..n,边:2*(n-2+1)
2 课后习题
15.2-1 m[i,k]+m[k+1,j]+ pi−1 pk pj
((A1A2)((A3A4)(A5A6)))…详见附件
15.2-2
F(A,s,i,j)
if i==j
return A[i];
if i+1==j
return mul(A[i],A[j]);
M1=F(A,s,i,s[i,j]);
M2=F(A,s,s[i,j]+1,j);
return mul(M1,M2);15.2-3 假设对任意k< n, P(k)>=c* 2k …
15.2-4 顶点: n2 边: (n3−n) /3 (无答案)
15.2-5
[i,j]=[i,i]+[i+1,j]=…=[i,j-1]+[j,j],所以连接(j-i)*2条
=>n(n-1)+(n-1)(n-2)+…+2+0= ∑i2 - ∑i (i=2..n)=n(n+1)(2n+1)/6-1- ∑n (i=2..n)= (n3−n) /3
15.2-6 数学归纳法
3 课后习题
最优子结构和子问题重叠
15.3-1RECURSIVE-MATRIX-CHAIN:O( n3n−1 ) time
enumerating:( 4n / n3/2 ) time
详见附件
15.3-2 略
15.3-3 具有
15.3-4 <1,1,2,3>
贪心:[1,3]=[1,1]+[2,3]+1*1*3=1*2*3+3=9
正确结果:[1,3]=[1,2]+[3,3]+1*2*3=1*1*2+6=8
15.3-5 最优子结构:问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解。
因为此时每种长度的切割数被限制,也就是说此时使用长度i时,会影响子问题的 li 大小,是相关的。[但个人认为可以建立[ rn ,L],L为 li 集合,但是子问题的状态数很大,几乎等于穷举了]
15.3-6 Dm =max{( Di - ci ) ri,j }=max{ Di ri,j - ci * ri,j },两个子问题相关,具有同样变量 ri,j
4 课后习题
LSC问题(最长公共子序列)O(mn)空间,O(m+n)时间重构
如果只计算长度:优化为一行多一点,但重构时间多
15.4-1 <1,0,1,0,1,0>,<1,0,0,1,1,0>,<1,0,1,0,1,1>,<0,1,0,1,0,1>
15.4-2 重构
if x[i]==y[i]
ReLCS(c,x,y,i-1,j-1)
print
else if c[i-1,j]>=c[i,j-1]
ReLCS(c,x,y,i-1,j)
else ReLCS(c,x,y,i,j-1)15.4-3 略,根据公示即可
15.4-4 计算LSC长度
- 只是用表c中2*min(m,n)表项+O(1)额外空间:
- min(m,n)表项+O(1)额外空间:
计算c[i,j]及之后结果需要用到c[i-1,k],k>=j-1或c[i,k],k<=j-1,所以空间一共一行+1,所以以min(m,n)为列数即可
详见附件
15.4-5 排序O(n lg n)与原字符串求LSC,O( n2 )
15.4-6
//Init:
cin>>a[]
c[0]=-1,c[1]=a[0]
for i=1 to n
l=find(c,len,a[i]);//二分查找,返回a[i]可加入位置(l)或不可(=len)
c[l]=a[i];//因为此时可以保证a[i]<原c[l],所以下一个数据加入时,若>a[i],即c[l],但小于c[l+1],可更新c[l+1],且能保证之后的解至少等于或好于现在的解;若>c[len],相当于为原c数组后再加数据,不影响解。唯一问题是,c中保留数据并不一定为解。
if l>len
len=l;//更新长度5 课后习题
最优二叉搜索树
表e[1..n+1,0..n],因为只包含伪关键字 dn , e[n+1,n],只包含伪关键字 d0 , e[1,0]
e[i,j]= qi−1 , (j==i-1) 或 min{e[i,r-1]+e[r+1,j]+w(i,j)}, (i<=j,令root[i,j]=r), (i<=r<=j)
w[i,j]=w[i,j-1]+ pj + qj , w[i,i-1]= qi−1
//个人理解,w为加入点的基本代价,而e为树深增加的代价
时间O( n3 )
15.5-1
if i<j
root: r=root[i,j]
lchild: root[i,r-1]
F(root,i,r-1)
rchild: root[r+1,j]
F(root,r+1,j)
else if i==j
root: r=i
lchild: d[i-1]
rchild: d[j]
else if i>j
leaf: d[j]15.5-2 略
15.5-3 重复计算,从 qi−1 初始+( pi + qi )+…+( pj + qj ),时间O(n)
但时间复杂度=O(n)O(n)(O(n)+O(n))=O( n3 ),不变
15.5-4 最优二叉搜索树,根root[i,j-1]<=root[i,j]<=root[i+1,j] 证算法时间为 O( n2 )
if i==j
root:j
else for root=root[i,j-1] to root[i+1,j]原:l=1 to n, i=1 to n-l+1, j=i+l-1, r=i to j ,时间O($n^3)
现:为了方便理解,我们书本侧向root表看,加了约束以后,1<=root1,j-1<=root[1,j]<=root2,j<=root[2,j+1]<=root3,j+1<=…<=rootn-l+1,n-1<=root[n-l+1,n]<=root[n-l+2,n]<=n。
所以每一层,计算长度为l,只需计算n次,所以一共O( n2 )
思考题
15-1 有向无环图中的最长简单路径 Path(s,t)[无答案]
DAG->拓扑排序 时间复杂度O(n+e)
Init: L(i)=-infinite, L(s)=0
L(t)=max{L(i)+w(i,t)}, if e(i,t) exist 时间复杂度O(e)
重构路径:if (L(u)-L(i)==w(i,u)) RePath(i)
所以整体O(n+e)
15-2 最长回文子序列
解1:s’=reverse(s)
时间O( n2 ),如果不需要输出具体内容的话可以减少到O(nlhn)(根据15.4-6)
解2:Manacher’s ALGORITHM: O(n)时间求字符串的最长回文子串
- 将奇数/偶数长度的回文子串都转换成奇数长度:在每个字符的两边都插入一个特殊的符号。比如 abba 变成 #a#b#b#a#, aba变成 #a#b#a#。 为了进一步减少编码的复杂度,可以在字符串的开始加入另一个特殊字符,这样就不用特殊处理越界问题,如$#a#b#a#
用数组 P[i] 记录以字符S[i]为中心的最长回文子串向左/右扩张的长度(包括S[i],也就是把该回文串“对折”以后的长度),P[i]-1正好是原字符串中回文串的总长度
S # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 #
P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1计算p[i]:id 为已知的 {右边界最大} 的回文子串的中心,mx则为id+P[id],也就是这个子串的右边界。如果mx > i,那么P[i] >= MIN(P[2 * id - i], mx - i)
- 当 mx - i > P[j] 的时候,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于 i 和 j 对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有 P[i] = P[j],见下图。
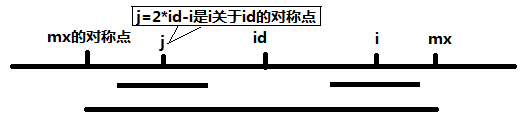
- 当 P[j] >= mx - i 的时候,以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中,但是基于对称性可知,下图中两个绿框所包围的部分是相同的,也就是说以S[i]为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 P[i] >= mx - i。至于mx之后的部分是否对称,就只能老老实实去匹配了。//其实此时,p[i]一定等于mx-i
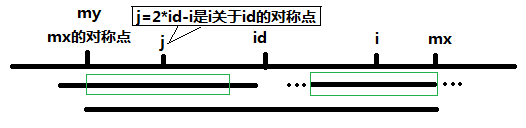
- 对于 mx <= i 的情况,无法对 P[i]做更多的假设,只能P[i] = 1,然后再去匹配了。
- 当 mx - i > P[j] 的时候,以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中,由于 i 和 j 对称,以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中,所以必有 P[i] = P[j],见下图。
- 代码如下:
//输入,并处理得到字符串s
int p[1000], mx = 0, id = 0;
memset(p, 0, sizeof(p));
for (i = 1; s[i] != '\0'; i++) {
p[i] = mx > i ? min(p[2*id-i], mx-i) : 1;
while (s[i + p[i]] == s[i - p[i]]) p[i]++;
if (i + p[i] > mx) {
mx = i + p[i];
id = i;
}
}
//找出p[i]中最大的15-3 双调欧几里得旅行商问题 O( n2 ),任何两点x坐标均不相同,d[i,j]=min{i->1->j},i>=j,求d[n,n]
- 根据x坐标排序,O(nlgn)
-
- 当 j < i-1时,d[i,j]=d[i-1,j]+a[i-1,i]
- 当 j = i-1时,d[i,j]=d[i,i-1]=min{a[i,k]+d[k,i-1]}, k=1..i-1
- 当 j = i 时,d[i,j]=d[i,i]=min{d[i,k]+a[k,i]}, k=1…i-1
详见附件
15-4 整齐打印,行尾额外空格符ex[i,j]: M−j+i−∑lk,(k=i..j) >0
Init: lc[i,j]=finite, (if ex[i,j]<0); 0, (if j==n && ex[i,j]>=0); ex[i,j], otherwise
w[k]=0, (if j==0); min{w[i-1]+lc[i,j], (i=1..k)}, (if k>0)
时间空间O( n2 )
详见附件
15-5 编辑距离
- Init: c[0,0]=0, c[i,0]=i*cost(delete), c[0,j]=j*cost(insert)
c[i,j]=min{c[i-1,j-1]+cost(copy), if x[i]==x[j];
c[i-1,j-1]+cost(replace), if x[i]!=x[j];
c[i-2,j-2]+cost(twiddle), if i,j>=2 && x[i]==x[j-1] && x[i-1]=x[j];
c[i-1,j]+cost(delete);
c[i,j-1]+cost(insert);
min{c[i,n]}+cost(kill), i=0..m-1, if i==m && j==n}
时间空间O(mn) - copy=-(+1)=-1, replace=-(-1)=+1, delete=-(-2)=+2, insert=-(-2)=+2
详见附件
15-6 公司聚会
dp[i,0]:不参加,dp[i,1]:参加
dp[i,0]= ∑max(dp[j,0],dp[j,1]) ,j是i的直接下属
dp[i,1]=w[i]+ ∑(dp[j,0]) ,j是i的直接下属
结果为max{dp[root,0],dp[root,1]}
O(n)
详见附件
15-7 译码算法
Li 链:存储(u,v)=声音 si 终点v,且 v0 通向每个v有一条路径,其边顺序标记&1,&2…&i,且在所有这样的路径中概率之积最大。
Init: L0 = v0 , P1 =1
Li 1. Add v, if v∉ Li && u∈ Li−1 && (u,v)= si
2. Update Pi , if v∈ Li && u∈ Li−1 && (u,v)= si && Pi−1∗P(u,v) larger
15-8 基于接缝裁剪(seam carving)的图像压缩 [无答案]
1. 开始位置m种,下一行*2(靠边),或*3,共m-1行
2. D[i,j]=min{D[i-1,j],D[i-1,j-1]}+d[i,j] O( m2 )
15-9 字符串拆分[无答案]
拆分点i到j
Dp[i,j]=0, if (j-i<=1); min{Dp[i,k]+Dp[k,j]}+L[j]-L[i]+1, k=i+1..j-1, otherwise. (mark[i,j]纪录当前拆分点k)
时间O( n3 ),空间O( n2 )
15-10 投资策略规划[无答案]
Dp[i,j]=max{Dp[k,j-1]- ∑ft∗r[t,j] , ( ft = f1 , if t==k; f2 , if t!=k)}, (k=1..n)
1. 所有钱投入单一投资,所以n年m种投资。求第j年最优投资,只需基于第j-1年的最优投资,假如存在第j年最优投资不包括第j-1年,则与原第j-1年解矛盾,所以。
[online]对任意的多重投资方案B,设法找到单一投资方案A,使得每年末A的资本不少于B,且每年当B不改投时A也不改投,B改投时A不一定改投,这样A方案的手续费一定低于B方案。首先考虑B每年都改投的情况,A只需购买当年收益最高的股票即可,由数学归纳法可证每年年底A的资产都比B高。然后证明B有些年份不改投的情况,假设B在连续的y年内不改投,那么将这连续的y年合并成一个加长的年,每只股票的在“这一年”的回报率等于每年回报率的乘积,手续费是相应的倍数,如此处理之后就变成了每一“年”都改投的情况。
2. 最优子结构问题:问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解。
3. O(n* m2 )
4. 因为投资金额限定+投资转移费用影响,最优解不一定包括子问题最优解
15-11 库存规划 [无答案]
第i月,库存j台
Dp[i,j]=min{Dp[i-1,k]+h(j)+( d[i]+j-k<=m ? 0 : (d[i]+j-k)*c )}, k=0…D
O( D2 *n)
15-12 签约棒球自由球员 注:可不签入球员
位置i,球员p=1..P[i],费用x,Dp[i,j]=max VORP
Dp[i,x]=max{ Dp[i-1,x], max{Dp[ i-1,x-p.cost ]+p.vorp}}, p=1..P[i]
时间O(NXP),空间O(NX).