数值分析案例：Newton插值预测2019城市(Asian)温度、Crout求解城市等温性的因素系数

数值分析案例：Newton插值预测2019城市(Asian)温度、Crout求解城市等温性的因素系数

一、实验目的及数据来源

1.研究问题的概述：

本文主要研究了插值方法在“城市温度变化预测”这一问题上的实际应用，以及使用构建线性方程组求解因素系数，进一步探索城市等温性的相关性因素。（采用的差值方法请参考之前的博客：Python：花了好久才写完的拉格朗日差值法和牛顿差商法的实现）

2.数据来源：

1. World Average Temperature(https://www.kaggle.com/efradgamer/world-average-temperature)

2. global environmental factors(https://www.kaggle.com/sadeka007/global-environmental-factors)

二、实验内容

第一部分：“采用Newton插值预测2019城市(Asian)温度”

Step 1：

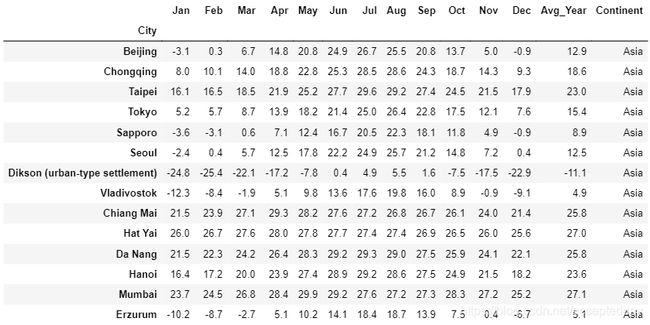
随机选择出一定数量的所属区域为亚洲的城市温度数据，并保证这些城市的地理位置信息在经度、维度上有一定的划分，达到全局采样的效果。*选取的城市如下：北京、重庆、台北、东京、札幌、首尔、Dikson、海参崴、清迈、合艾、孟买、岘港、河内、埃尔祖鲁姆。

代码如下：

# -*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import csv
import matplotlib.pyplot as plt
%matplotlib inline

path = 'DATA.csv'
data = pd.read_csv(path, index_col=0)
data.head(15)

Step 2：

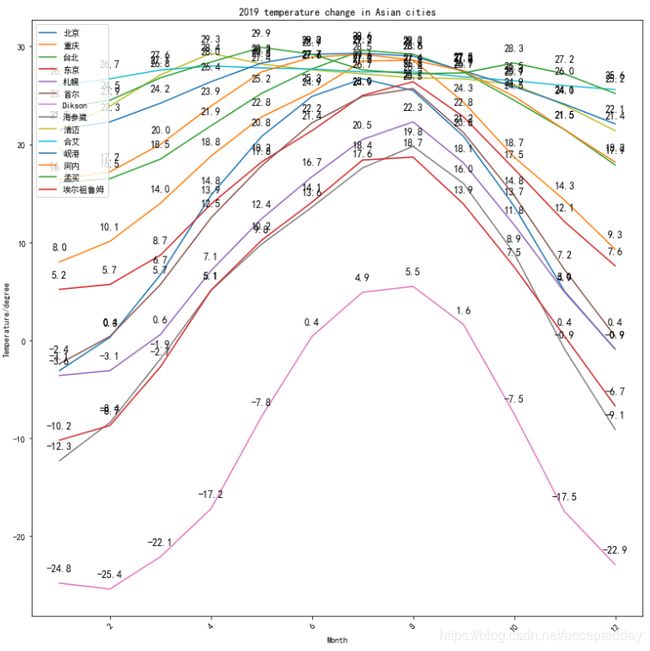
数据可视化，能够直观感受城市温度的对比，绘制城市温度折线图如下：

代码如下：

# 将csv文件格式转换为np.array格式，数据格式为float类型
Data = np.array(data.iloc[:,0:12], dtype=float) # 将数据转为float型
print(Data)

# 取出每个城市的12个月的温度统计数据
Beijing = Data[0,:]
Chongqing = Data[1,:]
Taipei = Data[2,:]
Tokyo = Data[3,:]
Sapporo = Data[4,:]
Seoul = Data[5,:]
Dikson = Data[6,:]
Vladivostok = Data[7,:]
ChiangMai = Data[8,:]
HatYai = Data[9,:]
DaNang = Data[10,:]
Hanoi = Data[11,:]
Mumbai = Data[12,:]
Erzurum = Data[13,:]

# 以折线图的方式可视化城市的年度温度变化数据
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]

plt.figure(figsize=(13, 13))
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.plot(x, Beijing,  ms=2, label="北京")
plt.plot(x, Chongqing,ms=2, label="重庆")
plt.plot(x, Taipei,  ms=2, label="台北")
plt.plot(x, Tokyo, ms=2, label="东京")

plt.plot(x, Sapporo, ms=2, label="札幌")
plt.plot(x, Seoul, ms=2, label="首尔")
plt.plot(x, Dikson, ms=2, label="Dikson")

plt.plot(x, Vladivostok, ms=2, label="海参崴")
plt.plot(x, ChiangMai,  ms=2, label="清迈")
plt.plot(x, HatYai,  ms=2, label="合艾")
plt.plot(x, DaNang, ms=2, label="岘港")

plt.plot(x, Hanoi,  ms=2, label="河内")
plt.plot(x, Mumbai,  ms=2, label="孟买")
plt.plot(x, Erzurum, ms=2, label="埃尔祖鲁姆")
plt.xticks(rotation=45)
plt.xlabel("Month")
plt.ylabel("Temperature/degree")
plt.title("2019 temperature change in Asian cities")
plt.legend(loc="upper left")


# 在折线图上显示具体数值, ha参数控制水平对齐方式, va控制垂直对齐方式
for y in [Beijing, Chongqing, Taipei, Tokyo,Sapporo,Seoul,Dikson,Vladivostok,
          ChiangMai,HatYai,DaNang,Hanoi,Mumbai,Erzurum]:
    for x1, yy in zip(x, y):
        plt.text(x1, yy + 1, str(yy), ha='center', va='bottom', fontsize=12, rotation=0)
plt.savefig("a.jpg")
plt.show()

Step 3：

数据划分，将城市温度的数据划分为训练集和测试集。为了保证数据的分层采样， 训练数据集：选取1、3、5、7、9、11月的温度； 测试数据集：选取2、4、6、8、10、12月的温度。

代码如下：

# train_data
Beijing_train = Data[0,[0,2,4,6,8,10]]
Chongqing_train = Data[1,[0,2,4,6,8,10]]
Taipei_train = Data[2,[0,2,4,6,8,10]]
Tokyo_train = Data[3,[0,2,4,6,8,10]]
Sapporo_train = Data[4,[0,2,4,6,8,10]]
Seoul_train = Data[5,[0,2,4,6,8,10]]
Dikson_train = Data[6,[0,2,4,6,8,10]]
Vladivostok_train = Data[7,[0,2,4,6,8,10]]
ChiangMai_train = Data[8,[0,2,4,6,8,10]]
HatYai_train = Data[9,[0,2,4,6,8,10]]
DaNang_train = Data[10,[0,2,4,6,8,10]]
Hanoi_train = Data[11,[0,2,4,6,8,10]]
Mumbai_train = Data[12,[0,2,4,6,8,10]]
Erzurum_train = Data[13,[0,2,4,6,8,10]]
# Test_data
Beijing_test = Data[0,[1,3,5,7,9,11]]
Chongqing_test = Data[1,[1,3,5,7,9,11]]
Taipei_test = Data[2,[1,3,5,7,9,11]]
Tokyo_test = Data[3,[1,3,5,7,9,11]]
Sapporo_test = Data[4,[1,3,5,7,9,11]]
Seoul_test = Data[5,[1,3,5,7,9,11]]
Dikson_test = Data[6,[1,3,5,7,9,11]]
Vladivostok_test = Data[7,[1,3,5,7,9,11]]
ChiangMai_test = Data[8,[1,3,5,7,9,11]]
HatYai_test = Data[9,[1,3,5,7,9,11]]
DaNang_test = Data[10,[1,3,5,7,9,11]]
Hanoi_test= Data[11,[1,3,5,7,9,11]]
Mumbai_test = Data[12,[1,3,5,7,9,11]]
Erzurum_test = Data[13,[1,3,5,7,9,11]] # 列表下标是从0开始的，下标0,2,4,6,8,10分别对应1、3、5、7、9、11月,而下标1,3,5,7,9,11分别对应2、4、6、8、10、12月

Step 4：

差值方法的选择，考虑到Lagrange 插值的龙格现象，而Hermite插值需要导数的参与，分段插值的拟合性较弱。综合考量，选择Newton差商法进行差值预测。

以北京市为例，预测2、4、6、8、10、12月的温度如下：

代码如下：

#Newton差商法
import numpy as np


def Qda_Table():
    for i in range(n+1):
        for j in range(n):
            if initial[i][j] is not None or i >= j + 2:
                continue
            else:
                initial[i][j] = (initial[i - 1][j] - initial[i - 1][j - 1]) / (
                        initial[0][j] - initial[0][j - i + 1])
            #  print("%d，%d的当前值为：" % (i, j) + str(initial[i][j]))


def calculate_factors(no, vari):  # 计算每次的相乘的自变量因子多项式
    factor = 1
    if no == 1:
        return factor
    else:
        for i in range(no-1):
            factor = factor * (vari-x[i])
    return factor


def final_calculate(k):
    result = 0
    for time in range(n):
        result = result + initial[time+1][time] * calculate_factors(time+1, v[k])
    return result



x = [1, 3, 5, 7, 9, 11]# 输入的月份
y = Beijing_train.copy()
n = len(x)
sum = 0
v = [2, 4, 6, 8, 10, 12]# 需要预测的月份
y_predict = [] # 用来存放预测月份的温度值

initial = []  # 初始化表格Table
for p in range(n+1):
    initial.append([])
    for q in range(n):
        initial[p].append(None)  # 生成n*n的二维列表，同时列表元素初始化为0
for k in range(n):
    initial[0][k] = x[k]
    initial[1][k] = y[k]
# print("初始化后的表格如下：")
# print(initial)  # 将x和y的值填入表格，完成Table的初始化。

Qda_Table()  # 计算每个位置的差商填表
QDA_table = np.array(initial).T  # 转置后输出结果
# print("最终的差商表格如下：")
# print(QDA_table)

for i in range(n):
    y_predict.append(np.around(final_calculate(i),decimals=4))
print("预测月份的温度信息如下：")
print(y_predict)

第二部分：“Crout求解分析城市的等温性影响因素系数”

Step 1：

选择第一部分城市所在国家(Korea, South、Japan、Turkey、India、Vietnam、Thailand、China、Russia)的环境因素数据，但由于环境因素数据包含众多的数据项，以及为了构建后面的线性方程组求解因素系数并分析其相关性，这里经查阅资料和筛选后，选取以下8项环境因素作为城市等温性因素分析的探索指标：*

elevation（海拔）

cropland_cover（农田覆盖率）

tree_canopy_cover（植被覆盖率）

rain_mean_annual（平均年降水量）

rain_seasonailty（季节性降水量）

temp_annual_range（年温度浮动范围）

cloudiness（云层量）

temp_mean_annual（年平均温度）

详细数据如下：

代码如下：

# 数据可视化
path = 'ENVI.csv'
source = pd.read_csv(path, index_col=0)
source.head(15)

Step 2：

构建线性方程组，假设可能性因素与等温性存在线性关系。根据计算得到的系数，初步分析其与等温性的相关性情况：假如|系数|近似为0，则相关性较低；|系数|大于等于0.5，将其判定为较高的相关性。方程求解采用Crout分解法。

自变量：elevation、cropland_cover、tree_canopy_cover、rain_mean_annual、rain_seasonailty、temp_annual_range、cloudiness、temp_mean_annual

因变量：isothermality

结果如下：

代码如下：

# Crout分解法求解
import numpy as np
import copy

def UAndL_Figure(k):
    # 按行计算U矩阵中Lj的值
    for j in range(mu):
        if j <= k:
            continue
        else:
            uj = A[k][j]/A[k][k]
            U[k][j] = uj
    # 根据U_Figure计算得到的li系数改变A矩阵
    for j in range(mu):
        j = j+k
        for i in range(nu):
            if j < nu-1:
                A[i][j+1] = A[i][j+1] - U[k][j+1] * A[i][k]
            else:
                continue


mu, nu = 8, 8 # 方程和自变量个数为8
source = np.array(source.iloc[:,0:9], dtype=float) # 将数据转为float型
A, L, U = [], [], []  # 初始化ALU矩阵
for p in range(nu):
    A.append([]), L.append([]), U.append([])
    for q in range(mu):
        x_in = source[p][q]
        A[p].append(x_in)
        if p == q:
            L[p].append(None), U[p].append(1)
        else:
            L[p].append(None), U[p].append(0)
A, L, U = np.array(A), np.array(L), np.array(U)


b_Const = source[:,[8]]  # 因变量y矩阵


for i in range(nu):
    UAndL_Figure(i)
L = copy.deepcopy(A)

y = np.dot(np.linalg.inv(L), b_Const)
x = np.dot(np.linalg.inv(U), y)
x = np.around(x,decimals=3)
# print("x的计算结果如下：")
# print(x)


t=[i for item in x for i in item]#将二维的X数据一维化
print("可能性因素的系数的结果如下：")
print(t)

Step 3：

经过Step 2的线性相关系数求解，我们得到与等温性相关程度较高的因素：Cropland_cover(农田覆盖率)、tree_canopy_cover(植被覆盖率)、temp_annual_range(年温度浮动范围)。可视化所有城市在这些指标项上的数据情况：

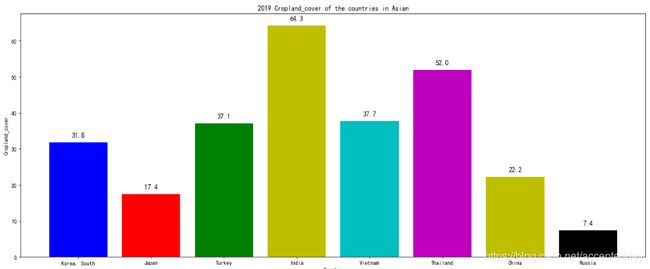
以cropland_over因素为例,代码如下：

# 将csv文件格式转换为np.array格式，数据格式为float类型
source = np.array(source.iloc[:,0:9], dtype=float) # 将数据转为float型
print(source)

# 设置matplotlib正常显示中文和负号
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False     

# 生成画布
plt.figure(figsize=(20, 8), dpi=70)
# 横坐标城市名字
country_name = ['Korea, South','Japan','Turkey','India','Vietnam','Thailand','China','Russia']
# 纵坐标海拔
y = source[:,1]
x=range(len(country_name))

plt.bar(x,y,color=['b','r','g','y','c','m','y','k','c','g','g'])
plt.xticks(x, country_name)
plt.xlabel("Country")
plt.ylabel("Cropland_cover")
plt.title("2019 Cropland_cover of the countries in Asian")

# 在折线图上显示具体数值, ha参数控制水平对齐方式, va控制垂直对齐方式
for x1, yy in zip(x, y):
    plt.text(x1, yy + 1, str(yy), ha='center', va='bottom', fontsize=12, rotation=0)

plt.show()

Step 4：

通过热力图分析潜在的因素，因为所选的国家个数以及选择的环境数据项局限性，并不能够很好的直接建立城市(Asian)等温性与其他环境因素之间的关系，所以*根据皮尔森相关系数(Pearson correlation coefficient)，用来反映两个变量线性相关程度的统计量。

该热力图的解释如下：

横轴指标分别为：Elevation、 rain_mean_annual、 rain_seasonailty、cloudiness、temp_mean_annual、Isothermality；纵轴数据分别为：Korea, South、Japan、Turkey、India、Vietnam、Thailand、China、Russia各个国家。

该热力图用于探索不同国家在相同的环境因素指标上是否具有相关性。可以发现Elevation和rain _mean_annual在不同国家的数据统计上具有潜在的相关性。

该热力图不包括Cropland_cover(农田覆盖率)、tree_canopy_cover(植被覆盖率)、temp_ annual_range(年温度浮动范围)因素分析。

代码如下：

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
f, ax = plt.subplots(figsize = (6,6))

#显示热力图
sns.heatmap(source[:,[0,3,4,6,7,8]], annot=True,fmt='.2f',cbar=True)
ax.set_title('City  Statistics ')
ax.set_xlabel('Index Of Environmental Attributes')
ax.set_ylabel('City name')

三、实验结果与分析

“采用Newton插值预测2019城市(Asian)温度”，该部分采用了Newton插值法进行对2019城市(Asian)温度的插值预测，经检验，插值的结果是比较好的，与实际统计的误差较小。实际的意义：当监测月份的温度数据缺失时，可采用Newton插值法进行数据的补全以供使用。

“Crout求解分析城市的等温性影响因素系数”，该部分为探索性实验，其结论可以作为研究和探索方向，但未经大量验证是不能够断章取义的。与等温性相关的可能性因素计算结果为：Cropland_cover(农田覆盖率)、tree_canopy_cover(植被覆盖率)、temp_annual_range(年温度浮动范围),也是符合地理常识的认知。

最后结合热力图分析，以皮尔森相关系数作为理论依据，分析潜在因素有：Elevation（海拔）和rain_mean_annual（年平均降水量），也是实验可以继续的因素方向。以及可以考虑非线性关系的构建，利用神经网络的易拟合性进行进一步的强化分析*。