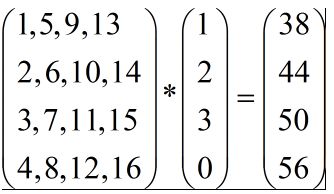OpenGL的列向量和OSG的行向量
在我们使用OpenGL和OSG的过程中,总会涉及到顶点坐标以及坐标的变换(通过向量和矩阵相乘),这其中经常会看到有人说在OpenGL中使用的是列向量,在OSG中使用的是行向量 ,由于行向量和列向量的不同导致在矩阵作乘法的时候有左乘和右乘之分,本文就这一问题作一个相对完整的解释。
- 行向量和列向量
1. 行向量和列向量的定义如下:
在线性代数
中,行向量是一个 1×
n
的矩阵
, 即矩阵由一个含有
n
个元素的行所组成。
在线性代数中,列向量是一个 n×1 的矩阵,即矩阵由一个含有n个元素的列所组成。
2. 左乘和右乘
说简单点,左乘(又称前乘)就是乘在左边(即乘号前),右乘(又称后乘)就是乘在右边(即乘号后)。比如说,A左乘E即AE,A右乘E即EA。
3.行向量和列向量的变换
由于向量实际上是某一维度为1的矩阵,那么根据矩阵乘法的规则,会出现下面的情况:
(1)行向量左乘矩阵
在图形学中一般矩阵都是4x4的,行向量一般设置为1x4的矩阵(齐次坐标)。当行向量左乘矩阵的时候 (1x4)* (4x4)得到的是一个1x4的行向量
(2)行向量右乘矩阵
这种情况,也就是(4x4)*(1x4),根据矩阵相乘的规则,这是不允许的
(3)列向量左乘矩阵
这种情况,也就是(4x1)*(4x4),根据矩阵相乘规则,这也是不允许的
(4)列向量右乘矩阵
这种情况,也就是(4x4)*(4x1),得到的是一个4x1的行向量
我们作三维的变化为的就是将一个坐标变换到另一个坐标,于是上面讨论的(1)(4)两种方式正好符合这一要求。根据上面的讨论有以下的结论:
行向量左乘还是右乘根本就是矩阵乘法规则的限制,行向量只能左乘而列向量只能右乘矩阵,这和三维图形学没有一点儿的关系。因此有人说OpenGL都是右乘、OSG都是左乘从结论上来说是对的,但是这和OpenGL以及OSG本身并没有半点关系,这只是矩阵乘法的定义。
- 行向量列向量以及在编程语言中的内存布局
假设有一个4x4的矩阵
M,我们现在有一个顶点的坐标是
v,通过
M矩阵的变换可以把它变为
v’,现在分别假设 v是行向量或者v是列向量,于是有以下两种情形:
(1)v是行向量 , 那么 v' = v*M
(2)v是列向量, 那么 v' = M*v
用那种方式来理解变换都是可以的。下面一段是OpenGL规范最早的设计者的一段话,可以从中知道他当时只是想使用列向量这种方式让图形学和数学上的表达一致,而" 欺骗” 读者说OpenGL使用的是列向量。
I'm the one responsible for the 'column-major ordering' used in OpenGL, so I'll try to explain what's going on to try to put this discussion to rest.
First, there are two issues that seem to be confused.
One issue is how matrices are stored in memory,
and the other is whether one treats vectors as rows of coordinates or as columns.
I'll dispense with the second issue first.
Recent mathematical treatments of linear algebra and related fields invariably treat vectors as columns (there are some technical reasons for this). For some reason, this has not been the case in computer graphics, where vectors were written as rows, thus transposing everything from standard mathematical usage. When I wrote the OpenGL spec, I decided to do my part to right this heinous inconsistency. Thus the spec is written with vectors treated as columns, with a matrix correspondingly applied on the left of a column.
The one difficulty was compatibility with the current GL, where vectors had been written as rows. So I come up with this subterfuge: say that matrices in OpenGL are stored in column major order. The point is that you could rewrite the spec with everything transposed (with vectors written as rows), and everything would be exactly the same as it was, including the row major ordering of matrices.
那么现在又有一个疑问:既然行向量和列向量并没有什么不同,那么为什么大家都在说在OpenGL中使用的是列向量而OSG中使用的是行向量呢? 答案就在于:
当使用C/C++语言进行描述矩阵和向量相乘的时候,使用行向量的理解方式和使用列向量的理解方式在内存中存储矩阵元素的时候有所不同,这就是真正的关键点所在。还是按之前的做法,假设现在坐标点是 (1,2,3, 0),通过矩阵M,变换为坐标值是(38,44,50,56)的点,对于这个变换来说,可以使用行向量和列向量来理解,这两种理解方式正好就是OSG和OpenGL的处理方式。
(1)使用行向量的方式来理解, 那么我们的矩阵是
double M[4][4] =
{
{1, 2, 3, 4},
{5, 6, 7, 8},
{9,10,11,12},
{13,14,15,16}
};
通过矩阵乘法知道 v = (1, 2, 3, 0) , 那么 v' = vM = (38, 44, 50, 56), 假设正好我们使用C/C++语言进行编码,由于C/C++语言中并没有矩阵这种类型,它使用二维数组来存储矩阵元素,并且在C/C++中使用的是 行主序的方式进行存储的,因此矩阵M在内存中如下图所示:
(2)使用列向量的方式来理解,那么我们的矩阵就不是上面的矩阵了,而是:
double M[4][4] =
{
{1, 5, 9, 13},
{2, 6, 10, 14},
{3, 7, 11, 15},
{4, 8, 12, 16}
};
在C/C++内存模型中,这个矩阵M如下所示:
可以看到使用行向量和列向量的区别,仅仅是内存布局的不同导致我们在理解行向量和列向量的时候有差异。
从上面的分析可以得出以下的几点结论:
(1)使用行向量或者列向量来理解OpenGL和OSG都可以,实际上行向量和列向量并没有任何的差别
(2)当使用列向量来理解变换的时候,所有的变换方式都是后乘(右乘),当使用行向量来理解变换的时候,所有变换的方式都是前乘(左乘)
(3)OpenGL为了表现它是使用的列向量,所有的矩阵设计为列主序的方式,因此当我们在进行变换的时候,需要注意要将矩阵按C/C++语言内存布局的方式存储,也就是说假设有一个平移矩阵,平移量Tx,Ty,Tz应该处在的位置是数组的第 4,8,12位置处
这种处理方式在C/C++中会显得十分别扭,因为这几个平移变量的位置不连续,这也是为什么很多三维库都使用 行主序(行向量)方式的原因,因为如果使用行向量的方式,那么这三个行向量的位置正好是相邻的,和C/C++语言的存储方式一致。 不过OpenGL也提供了用来接收行主序方式的矩阵的函数:
glLoadTransposeMatrixf
glLoadTransposeMatrixd double xarray[4][4] =
{
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
};
osg::Matrixd mat;
mat.set((double*)xarray);
//x12 = 7
double x12 = mat(1, 2);