图的匹配--二分图，一般图以及二分图的边覆盖、独立集和顶点覆盖

最经典的二分图匹配问题：

这个问题可以像下面这样转化为图论模型来分析。我们可以像下面这样来定义无向二分图，$G=(U\cup V,E)$。

$U$是代表计算机的顶点集合，$V$代表任务的顶点集合，对于任意的$u\in U$,$v\in V$，计算机$u$能处理任务$v$，那我们就在$u,v$之间连一条边，$(u,v)\in E$。

而$G$中满足两两不含公共端点的边集合$M\subseteq G$的基数$|M|$的最大值，就是我们所要求的最大的任务个数。

图论术语中，我们将这种两两不含公共端点的边集合$M$为匹配，而元素最多的$|M|$称为最大匹配。当最大匹配的匹配数满足$2|M|=|V|$时，又称为完美匹配,也就是每个点都匹配上了。特别地，二分图中的匹配又称为二分图匹配。像这道题目一样，二分图匹配常常在指派问题的模型中出现。那么这道题目应该如何求解呢？

解法1：最大流模型

最大流简介，我们将二分图改成一个有向图，

将原图中的所有无向边$e$改成有向边，方向从$U$到$V$容量为1。增加源点$s$和汇点$t$，从$s$向所有的顶点$u\in U$连一条容量为1的边，从所有的顶点$v\in V$向$t$连一条容量为1的边。

这样变形得到的新图$G^{\prime }$中最大$s-t$流的流量就是原二分图$G$中最大匹配的配数，而$U-V$之间流量为正的边集合就是最大匹配。该算法的复杂度为$〇(|V||E|)$。

解法2：匈牙利算法

盗一张网图，很久之前截下来的，忘了从哪。。。

先逐一匹配，然后有人没有妹子的时候进行回溯，看能不能腾出来一个妹子，腾到不能腾为止。


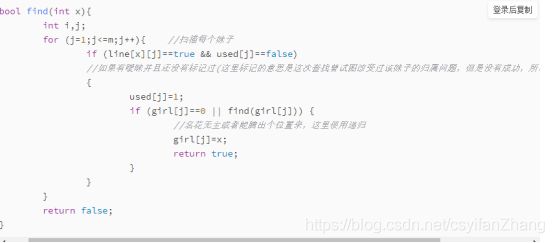
注意，对每个boy，used数组都要重新初始化，表示的是在本次寻找中是否试图更改过该girl的归属问题，如果更改成功了那么就有返回解，但是如果更改失败了，这个girl就不需要白费力气了。对男三来说，他会回溯到男2，男2此时要跳过对女2的判断，只需要向下看女3是否可以过度到他手里，如果可以就会返回true

一般图匹配

如果把这个当作一个以学生为顶点，朋友关系为边的图，就可以把这个问题转为求对应的图的最大匹配数的问题。之前的问题顶点有计算机和任务之分，所以得到的是二分图，而这里得到的却不一定是二分图。这种问题被称为一般图匹配问题，它不能像二分图一样转为最大流问题进行求解。求解一般图匹配问题可以使用Edmonds算法等高效的算法。只不Edmonds算法的实现较为复杂，所以程序设计竞赛中较少出现这类问题。如果把模型转化成了匹配问题，可以先看看事实上是否是二分图匹配，如果确实不是二分图，而用其他方法又可能行不通时，我们可以用利用Tutte矩阵来计算一般图最大匹配的匹配数。

匹配、边覆盖、独立集和顶点覆盖

注意，对二分图而言，最大匹配数目等于最小的顶点覆盖数目，因此，我们可以高效地求解二分图的最大独立集和最小顶点覆盖，事实上，这类问题也常常出现在程序设计竞赛当中。相对的，如果把问题转为一般图的最大独立集或最小顶点覆盖，则无法直接、高效地求解，有必要从其他角度重新思考。

一个无向图是二分图的充要条件是不存在奇环。

常用技巧：棋盘图黑白染色形成二分图&&网格x-y形成二分图。

S向左侧xi连边，右侧yi向T连边。

二分图题目先转化成对应二分图模型，再对应转化为网络流。

标准建图：边权全为1。

1.最大匹配=最大流（最大匹配就是匹配边数最大）牛与食物

2.最小顶点覆盖=最小割（最小覆盖就是选择最少的点使每条边至少有一个端点被选中，选点类比割边就是最小割二维小行星快速打击，木板填泥地）

3.最大独立点集=总点数-最小覆盖（最大独立集就是最大的点集，集合中的点两两不连接。独立集中不能有边，每个两点匹配只能选一点，所以把最大匹配数减去后就是答案。幼儿园找互相认识的学生问题，优美的拆散早恋）

4.最小路径覆盖：在DAG找尽量少的路径，使每个节点恰好在一条路径上(点不相交)。

做法：将每个点拆开分别放入xy集合中，如果u到v有一条边，则连边u,v`，然后二分图最大匹配。

初始未匹配ans=n即每个点单独为一条路径，匹配一条说明连了两点，ans-1，所以最终ans=N-最大匹配。

5.二分图带权匹配：要求完美匹配就跑费用流，不要求完美匹配就跑流量不固定的费用流（spfa时若最短路费用对答案没贡献就返回失败）。

6.【最大权闭合子图】

S向正权点连边，负权点向T连边，0不管，原边全部转为正无穷（节点权值全部转到了与S、T的连边上）。

最有解雇方案

割掉与S相邻的边就是这个点舍弃了S，成为T中的正权点(离开闭合子图)；割掉与T相邻的边就是这个点舍弃T，成为S中的负权点(进入闭合子图)。(割的值与答案密切相关)

因为每条路径必须有割，所以对于所有依赖关系要么与T相邻断边(把依赖对象收进来)，要么与S相邻断边(把依赖源扔掉)。

最大权闭合子图的权值=所有正权点之和-最小割

可以简单理解为理想可以收入所有正权点，舍弃所有负权点，然而实际上需要扔些正权点，捡一些负权点(即每条路径有一割)。

对于扔掉的正权点，就是减去割去的S邻边权值；对于捡起来的负权点，其实就是加上负权=减去割去的T邻边的权值。

所以权值=正权点之和-割，最小割对应最大权闭合子图。