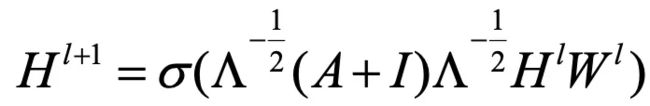(DGNN读书笔记)Skeleton-Based Action Recognition with Directed Graph Neural Networks-DGNN读书笔记
Skeleton-Based Action Recognition with Directed Graph Neural Networks-DGNN读书笔记
- Skeleton-Based Action Recognition with Directed Graph Neural Networks
- 1.摘要
- 2. 引言
- 3. 理论
- 3.1骨骼信息
- 3.2图构造
- 3.3双向图神经网络(DGNN)
- 3.3.1双向图神经网络 block
- 3.3.2DGN块的实现
- 3.3.3自适应DGN block
- 3.3.4时间信息模型
- 3.3.5双流框架(Two-Stream Framework)
- 4.实验
- 4.1数据集
- 4.2Ablation Study
- 4.2.1 DGN block
- 4.2.2Adaptive DGN blocks
- 4.2.3Two-Stream framework
- 4.2.4 对比其他SOTA方法
Skeleton-Based Action Recognition with Directed Graph Neural Networks
代码:https://github.com/kenziyuliu/Unofficial-DGNN-PyTorch
论文:http://openaccess.thecvf.com/content_CVPR_2019/papers/Shi_Skeleton-Based_Action_Recognition_With_Directed_Graph_Neural_Networks_CVPR_2019_paper.pdf
1.摘要
简单的说就是利用骨骼数据在动作识别上已经有了飞速的发展,骨骼和关节两类数据分别对动作识别有着重要的作用。如何更好的利用骨骼和关节数据去识别动作,就是这篇论文要讨论的问题。在这项工作中,作者基于自然人体关节和骨骼之间的运动学相关性,将骨骼数据表示为有向无环图(DAG)。 专门设计了一种新颖的定向图神经网络,用于提取关节,骨骼及其关系的信息,并根据提取的特征进行预测。此外,为了更好地适应动作识别任务,基于训练过程使图的拓扑结构具有自适应性,从而带来了显著的改进。 此外,利用骨骼序列的运动信息并将其与空间信息结合,以进一步增强两流框架中的性能。并且在两大数据集NTU-RGBD和 Skeleton-Kinetics中都取得了SOTA
2. 引言
简单介绍了一下动作识别的应用,对比与传统的动作识别方法,基于骨骼数据的识别方法可以抵抗人体比例,运动速度,摄像机视点和背景干扰等变化所带来的识别阻碍。而且骨骼数据目前可以很容易通过传感器以及姿态估计算法获得。深度学习在此任务上的三大方法:
1.GNN
数据主要是基于图形
2.RNN
数据主要是基于矢量序列
3.CNN
数据主要是基于伪图像
有人证明过骨骼数据更有利于动作识别。因为人类自然地根据骨骼在人体中的方向和位置来评估动作,而不是关节的位置。此外,已经证明关节和骨骼信息是彼此互补的,并且将它们组合可以导致识别性能的进一步提高。 对于自然的人体,关节和骨骼牢固地结合在一起,每个关节(骨骼)的位置实际上是由它们连接的骨骼(关节)确定的。我的理解是:利用好关节(骨骼)与关节(骨骼)的相关性,可以提升识别的效果。
论文中举了个例子:例如,肘关节的位置取决于上臂骨的位置,同时也决定了前臂骨的位置。现有的基于图的方法通常将骨骼表示为一个无向图,并用两个独立的网络对骨骼和关节进行建模,而这两个网络不能充分利用关节和骨骼之间的这些依赖性。一种很简单的解决办法:把骨骼描述为一个有向无环图,关节作为顶点,骨骼作为边.
除此之外,又存在一个问题,最初的骨骼是根据人体结构手工设计的,这对于动作识别任务来说可能不是最理想的。这一点刚开始很不好理解,论文中举了一个例子:简单的说就是拥抱或者握手等考察双手依赖性较强的动作时,这种双手的依赖性并不能在人工设计的骨骼结构中体现出来。解决方法:采用adaptive graph。
这篇文章也和其他论文一样,采用了two-stream框架。即 spatial stream 和motion stream
3. 理论
思路:原始骨架数据是一系列帧,每个帧包含一组关节坐标。对于给定的骨骼序列,我们首先根据关节的二维或三维坐标提取骨骼信息。然后,将每个帧中的关节和骨骼(空间信息)表示为图中的顶点和边,并将这些顶点和边送入有向图神经网络(directed graph neural network, DGNN)中,以提取行为识别的特征。最后,将与空间信息相同的图形结构表示的运动信息提取并与two-stream框架中的空间信息相结合,进一步提高性能。
3.1骨骼信息
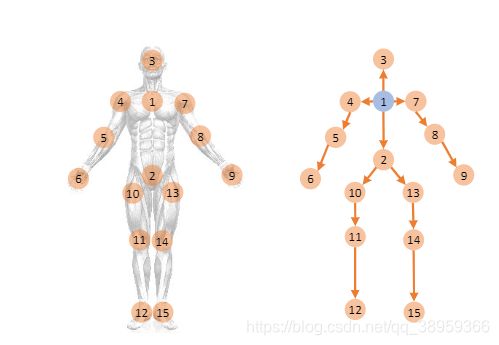
例如上面这张图片,编号处为关节点,很容易想出两个关节点 v 1 , v 2 v1,v2 v1,v2中间即为一根骨骼。所以在论文中的对于关节点 v 1 = ( x 1 , y 1 , z 1 ) v_1=(x_1,y_1,z_1) v1=(x1,y1,z1)和关节点 v 2 = ( x 2 , y 2 , z 2 ) v_2=(x_2,y_2,z_2) v2=(x2,y2,z2),构成了由 v 1 , v 2 v1,v2 v1,v2连接的骨骼 e ( v 1 , v 2 ) = ( x 1 − x 2 , y 1 − y 2 , z 1 − z 2 ) e_(v1,v2)=(x_1-x_2,y_1-y_2,z_1-z_2) e(v1,v2)=(x1−x2,y1−y2,z1−z2)
3.2图构造
在这项工作中,作者将骨骼数据表示为一个有向无环图(DAG),其中关节为顶点,骨骼为边。每个顶点的方向是由顶点和根顶点之间的距离决定的,其中更靠近根顶点的顶点指向离根顶点更远的顶点。这里,根顶点被定义为骨架的重心。 因为被证明离人体中心较远的关节通常由离中心较近的相邻关节控制。
总结一下: e e e表示骨骼(边)集合, v v v表示关节点(结点)集合, g ( e , v ) g(e,v) g(e,v)某一帧的骨骼数据。 S = ( g 1 , g 2 . . . ) S=(g_1,g_2...) S=(g1,g2...)表示某个视频内所有帧的骨骼数据。(这很好理解)
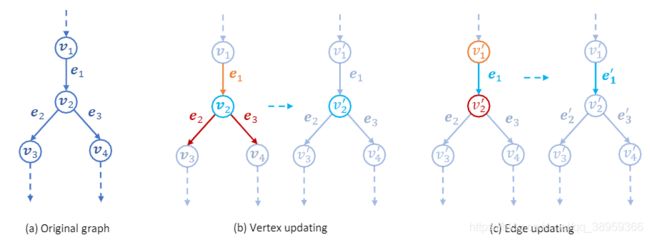
图中演示的就是边(结点)的更替。
3.3双向图神经网络(DGNN)
由于我们已经将骨骼数据表示为一个有向图,现在的问题是如何提取图中包含的信息进行动作分类,特别是如何利用图中关节和骨骼之间的依赖关系。在本文中,作者提出一种双向图神经网络(DGNN)来解决这个问题。
3.3.1双向图神经网络 block
双向图神经网络是最基本的块。包含了两类函数:**两个更新函数 h v , h e h~^v,h^e h v,he和两个聚合函数 g e − g^{e-} ge−和 g e + g^{e+} ge+ 。 更新函数 : 根据相邻结点和边更新当前结点和边的属性 。聚合函数用于讲连接到一个顶点的多个输入(输出)边中包含的属性聚合起来。文中给出的原因是:
1.这是因为连接到每个顶点的传入(传出)边的数量是变化的,而参数的数量是固定的。
2.相连的边是无序的。
基于以上两点:我们应该对其输入的边的排列不变,并且可以接受可变数量的参数,例如平均池、最大池和元素求和。所以引入了聚合函数。
具体的数学描述如下:
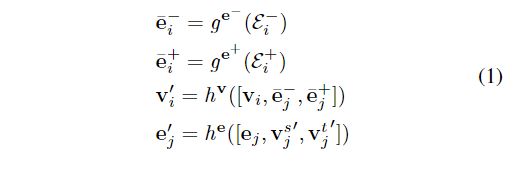
论文中给出的解释是:
step1: e ˉ i − \bar e_i^- eˉi−:对于每一个结点 v i v_i vi,所有入边输入聚合函数 g e − g^{e-} ge−
step2: e ˉ i + \bar e_i^+ eˉi+:类似于步骤1,所有的出边输入聚合函数 g e + g^{e+} ge+
step3:每一个结点 v i v_i vi,以及入边 e ˉ i − \bar e_i^- eˉi−出边 e ˉ i + \bar e_i^+ eˉi+共同输入更新函数 h v h^v hv中
step4:每一条边 e j e_j ej,以及源结点 v j s v_j^s vjs,目标结点 v j t v_j^t vjt共同输入更新函数 h e h^e he中
这个可以被称为结点更新过程和边更新过程,论文中提出: 通过大量的实验,作者选择了average pooling作为聚合函数来处理输入边和输出边,并选择了single fully-connected层作为更新函数。
3.3.2DGN块的实现
我对论文的这一part的内容做了一个小小的概括。首先我们要知道一个概念,这一个概念也在图神经网络中极为常见。对于下面一个图:
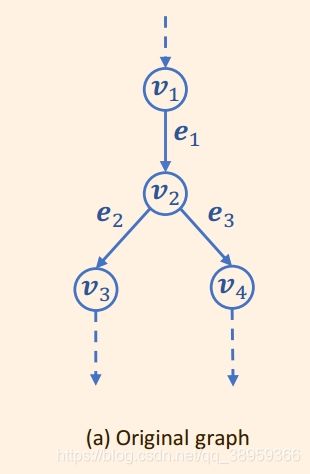 对应的关联矩阵如下所示:
对应的关联矩阵如下所示:
 我的理解是:(对于矩阵A 三行四列,对应的是三个结点四条边。如果第i条边是第j个结点的出边,aij的值为-1;若为入边,aij的值为+1)
我的理解是:(对于矩阵A 三行四列,对应的是三个结点四条边。如果第i条边是第j个结点的出边,aij的值为-1;若为入边,aij的值为+1)
对于图卷积网络,这是最基本的公式。 ∧ \wedge ∧这个符号代表的是度矩阵。度矩阵的定义如下:
∧ i i = ∑ j A i j + ∈ \wedge_{ii}=\sum_j A_{ij}+\in ∧ii=j∑Aij+∈
其中 ∈ \in ∈是为了避免被零除。在这篇论文里, A ∼ = A Λ − 1 A^\sim = AΛ^{−1} A∼=AΛ−1。这样做的目的是:使用的聚合函数是平均池化操作,关联矩阵需要进行规范化。
那么公式1就可以改写为: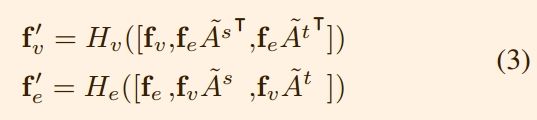
H代表的是单全连接层,与传统的卷积层类似,我们在每个DGN块之后添加一个BN层和一个ReLU层。
3.3.3自适应DGN block
DGN块的输入图形是根据人体的自然结构手工设计的。我们建议此配置可能不适用于动作识别任务。例如,左手和右手之间没有联系;然而,对于许多动作,如拍手和拥抱,两只手之间的关系对于识别是很重要的。为了使图的构造更具灵活性,传统的方法是在训练过程中通过学习图的拓扑结构来构造自适应图.
例如,Yan等人在原始邻接矩阵上应用注意图,为不同的边分配不同的重要性级别。但是这种方法基于矩阵的乘法更新邻接矩阵, A = P A o A = PAo A=PAo.缺陷:初始为0 乘法做了多少次,依然为0。即例如对于手部,初始并未考虑。更新数次后依然为考虑。为什么不能用A=A0+P呢?这样不就解决了乘法的缺陷。。
Shi等人直接将邻接矩阵设置为网络的参数。为了稳定训练过程,他们设置了A = Ao + P,其中P的大小与Ao相同,初始值为0。这样,在学习过程中,如果需要,可以通过参数P来添加新的边。然而,由于Ao是不可修改的,我们无法删除我们不想要的边,这也降低了模型的灵活性。但是,如果我们去掉Ao,那么不受任何限制的直接学习图结构,这样将会降低性能。
在这个工作中,作者发现在Shi中有Ao或者没有Ao的情况之间的区别主要在于训练过程的开始( 注意这里的A表示关联矩阵,而不是像之前工作中那样表示邻接矩阵 ) 。这个结果是直观的,因为在训练过程的开始阶段,存在更多的不确定性;因此,该模型约束少,但参数多,容易收敛到局部最优。
综合一下,.作者在本文所提到的做法是:加入一个具有固定拓扑的图,相当于基于人体先验知识对模型进行正则化,使模型收敛到全局最优。在此基础上,提出了一种简单有效的解决问题的策略。我们直接将A设为模型的参数,但在前几个训练阶段进行了修正。在早期固定图形结构可以简化训练,而在后期取消固定可以为图形构建提供更大的灵活性
3.3.4时间信息模型
前面的工作主要是对某一帧所操作的,并未考虑时间约束。这一part主要是将时间约束考虑上。在STGCN中,时间约束的考虑很据特色。在这篇论文中,在受到 pseudo-3D CNN(先用二维卷积对空间信息进行建模,再用一维卷积对时间信息进行建模)的启发下,在更新每个DGN块中关节和骨骼的空间信息后,作者采用沿时间维的一维卷积对时间信息进行建模。这很容易实现,因为所有帧中的相同关节或骨骼可以自然组织为一维序列。
与DGN块类似,每个1D卷积层后面都有一个BN层和一个ReLU层,形成一个时间卷积块(TCN)。DGNN的总体结构有9个单元,每个单元包含一个DGN块和一个TCN块。单元输出通道数分别为64,64,64,128,128,128,256,256 和 256。 最后添加一个global-averagepooling layer和softmax layer 用于分类预测。
3.3.5双流框架(Two-Stream Framework)
有些动作,比如站着和坐着,很难从空间信息中识别出来。传统的基于rgb的动作识别方法通常使用光流场来描述视频的运动信息,计算连续帧之间的像素运动信息。在这些方法的启发下,我们提取了关节的运动和骨骼的变形来帮助识别 。简单的说数学描述如下:
m v t = v t + 1 − v t ( 关 节 ) m e t = e t + 1 − e t ( 骨 骼 ) m_{vt} = v_{t+1} − v_t (关节) \\ m_{et} = e_{t+1} − e_t(骨骼) mvt=vt+1−vt(关节)met=et+1−et(骨骼)
之前有提到过: 在某一帧,对于关节点 v 1 = ( x 1 , y 1 , z 1 ) v_1=(x_1,y_1,z_1) v1=(x1,y1,z1)和关节点 v 2 = ( x 2 , y 2 , z 2 ) v_2=(x_2,y_2,z_2) v2=(x2,y2,z2),构成了由 v 1 , v 2 v1,v2 v1,v2连接的骨骼 e ( v 1 , v 2 ) = ( x 1 − x 2 , y 1 − y 2 , z 1 − z 2 ) e_(v1,v2)=(x_1-x_2,y_1-y_2,z_1-z_2) e(v1,v2)=(x1−x2,y1−y2,z1−z2)
公式中的t就代表着不同的帧。相邻两帧的差值就代表着骨骼和关节的变动。然后,将运动图输入另一个DGNN,以对动作标签进行预测。通过添加softmax层的输出分数,最终结合了两个网络得到结果。
学习笔记:
1)使用骨骼数据带入模型得到结果
2)使用关节数据带入模型得到结果
3)综合两者,得出最终结论
4.实验
4.1数据集
作者仍然是在Skeleton-Kinetics和NTU-RGBD进行实验。
4.2Ablation Study
4.2.1 DGN block
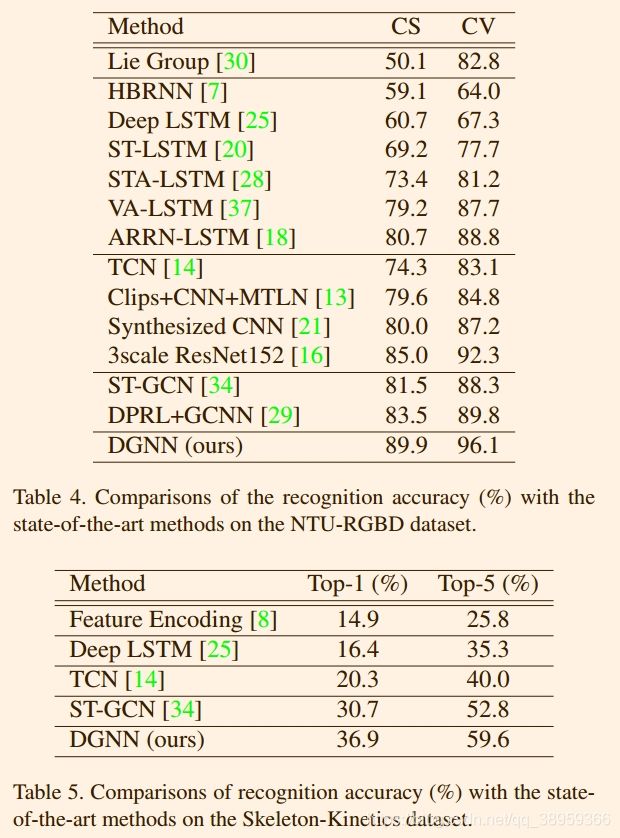
简单说明,在本节中,作者将检验所提出的DGNblock、自适应图策略和双流架构的有效性。以识别精度作为评价指标。由于ST-GCN中的图结构乘以一个MASKED,我们也固定了DGNN的图结构,并使用一个MASKED与关联矩阵相乘以进行公平比较。得到的模型称为MASKED DGNN,结果如下:
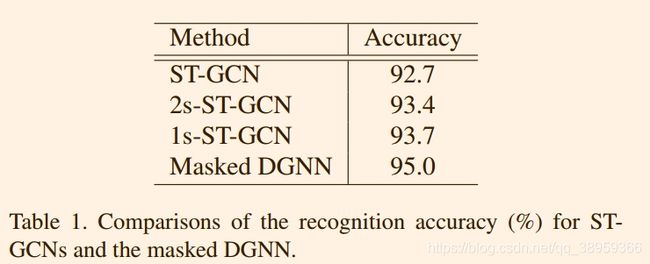
4.2.2Adaptive DGN blocks
1)与ST-GCN类似,我们将MASKED P乘以原始关联矩阵a,将其设置为模型参数并初始化为1(表中标记为PA)
2)我们将P设置为residual connection,初始化为0并添加到a(标记为P + a)
3)我们直接将关联矩阵设置为参数P,初始化参数为A(标记为P0)
4)将关联矩阵设为模型的参数,初始化为A,但在前10个epoch固定(标记为P10)

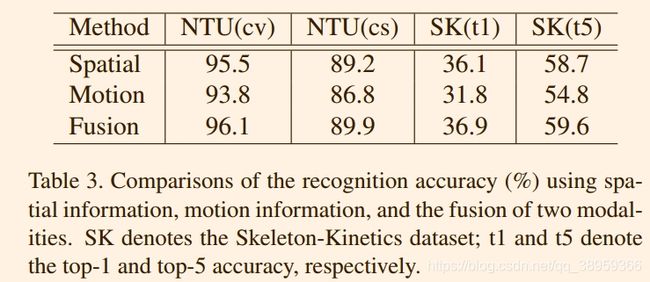
4.2.3Two-Stream framework
空间信息、运动信息和融合两种模式识别准确率的比较(%)。SK表示骨架动力学数据集;t1和t5分别表示top-1和top-5的准确率