最短（长）路总结

最短（长）路总结

最短路

最短路问题主要分为两类，第一类是单源最短路，第二类是多源最短路

单源最短路

一般是使用dijkstra算法解决

多源最短路

多源最短路也要分为两类，第一类是求每个源点到某个点的最短路，第二类是求所有源点中能到达某个点的最短路。
对于第一类问题需要根据题面来判断选择哪一类算法，如果需要边加点边判断，一般是选择离线+floyed算法处理；如果没有特殊要求可以选择对每个源点跑一次单源最短路；如果对时间要求比较高的就只能选择优化过的dijkstra算法。
第二类问题一般是建立一个超级源点，从超级源点向题目要求的源点连一条有向边，然后跑一次单源最短路即可。

Floyed算法

Floyed算法一般是用来求解多源最短路的第一类问题，其复杂度是O(n^3)，一般节点数超过500这个算法基本就炸了，不过要是题目给100s那我也没话说。

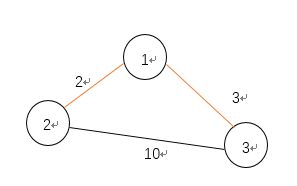
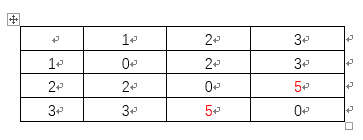
基本思想就是在原来的图上加点，加入一个点然后就去更新一下每个点对之间的距离。

加入点1后


模板

//floyed一般是用邻接矩阵存图
void floyed(){
    for(int v=1;v<=n;v++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(g[i][j]>g[i][v]+g[v][j]+tax[v])
                {
                    g[i][j]=g[i][v]+g[v][j]+tax[v];
                    path[i][j]=path[i][v]; //记录路径 
                }
                //else if(g[i][j]==g[i][v]+g[v][j]+tax[v])
                  //  path[i][j]=min(path[i][j],path[i][v]); 题目要求
            }
        }
    }
} 

dijkstra算法

dijkstra算法多种多样，就讲一下经典的dijkstra算法吧
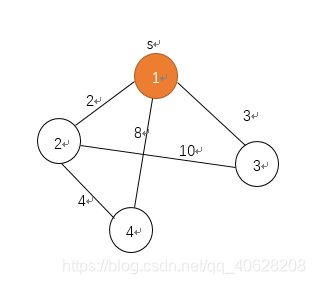
dijkstra算法的思想是从源点s出发，找到离源点s最近的点u1，然后再去找离s或者u1中最近的点u2，就这样一直把点找完

dijkstra图示(点1是源点)

就这样就可以得到从源点1到其他所有点的最短距离

经典dijkstra模板
复杂度O(n^2)

void dijkstra(int u,int n){
    memset(vis,0,sizeof(vis));
    for(int i=0;i<=n;i++)dis[i]=maxn;
    dis[u]=0;
    for(int i=0;i<=n;i++){
        int k=-1;
        int mindis=maxn;
        for(int j=0;j<=n;j++){
            if(!vis[j]&&dis[j]<mindis){
                k=j;
                mindis=dis[j];
            }
        }
        if(k==-1)break;
        vis[k]=true;
        for(int j=0;j<=n;j++){
            if(!vis[j]&&dis[j]>dis[k]+g[k][j])
                dis[j]=dis[k]+g[k][j];
        }
    }
}

堆优化dijkstra模板
复杂度:O( ( n + m ) log n )

#include
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e5 + 10;
const ll inf = (ll)1e16;

vector <pii> V[N];
int n, m;
bool vis[N];
ll dis[N];

struct Node{
	int id;
	ll d;
	Node(){}
	Node(int id, ll d):id(id),d(d){}
	bool operator < (const Node &A)const{
		return d > A.d;
	}
};

void dijkstra(int st){
	for(int i=1; i<=n; i++){
		vis[i] = 0;
		dis[i] = inf;
	}

	dis[st] = 0;
	priority_queue<Node> Q;
	Q.push(Node(st, 0));
	Node nd;

	while(!Q.empty()){
		nd = Q.top(); Q.pop();
		if(vis[nd.id]) continue;
		vis[nd.id] = true;
		for(int i=0; i<V[nd.id].size(); i++){
			int j = V[nd.id][i].first;
			int k = V[nd.id][i].second;
			if(nd.d + k < dis[j] && !vis[j]){
				dis[j] = nd.d + k;
				Q.push(Node(j, dis[j]));
			}
		}
	}
}

int main(){
	int x, y, z, st, ed, cas = 0;
	scanf("%d", &cas);
	while(cas--){
		scanf("%d%d%d", &n, &m, &st);
		for(int i=1; i<=n; i++) V[i].clear();
		while(m--){
			scanf("%d%d%d", &x, &y, &z);
			V[x].push_back(make_pair(y, z));
			//V[y].push_back(make_pair(x, z));
		}
		dijkstra(st);
		for(int i=1; i<=n; i++)
			if(i==1) printf("%d", dis[i]);
			else printf(" %d", dis[i]);
	}
}

配对堆优化dikstra模板
复杂度:O( n log n + m )

#include
#include
using namespace std;
using namespace __gnu_pbds;
typedef long long ll;
const int mn = 100005;
const int maxn = 200005 ;
const int inf = 2147483647;
typedef __gnu_pbds::priority_queue< pair<int,int> ,\
greater< pair<int,int> >,pairing_heap_tag > heap;
heap::point_iterator id[mn];//记录下每个点的迭代器 
heap q;

inline int read(){
    int x=0;
    char ch=getchar();
    while(ch>'9' || ch<'0') ch=getchar();
    while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
    return x;
}

struct edge{int to, next, dis;};
edge e[maxn * 2];
int head[mn], edge_max;
int n, m, st, dis[mn];

void add(int x, int y, int z){
    e[++edge_max].to=y;
    e[edge_max].dis=z;
    e[edge_max].next=head[x];
    head[x]=edge_max;
}

void dij(int x){
    for(int i=1; i<=n; i++) dis[i] = inf;
    dis[x]=0;
    id[x] = q.push(make_pair(0, x));//每次push会返回新加入点的迭代器 
    while(!q.empty()){
        int now = q.top().second;
        q.pop();
        for(int i=head[now]; i; i=e[i].next){
            if(e[i].dis+dis[now] < dis[e[i].to]){
                dis[e[i].to] = dis[now]+e[i].dis;
                if(id[e[i].to]!=0) //如果在堆中 
                    q.modify(id[e[i].to], make_pair(dis[e[i].to], e[i].to));//修改权值 
                else id[e[i].to] = q.push(make_pair(dis[e[i].to], e[i].to));//加入堆 
            }
        }
    }
}
int main(){
    int x, y, z;
    n=read(), m=read(), st=read();
    for(int i=1; i<=m; i++){
        x=read(), y=read(), z=read();
        add(x, y, z);
    }
    dij(st);
	for(int i=1; i<=n; i++)
		if(i==1) printf("%d", dis[i]);
		else printf(" %d", dis[i]);
}

最后再讲一个spfa算法，dijksra算法如果碰到负环就GG了，而spfa算法可以判断负环，但是spfa算法不稳定，复杂度不一定，大部分时候都是dijkstra比spfa算法更优，不排除偶尔出题人的小心思。

spfa算法模板

bool SPFA(int src){
    memset(vis,0,sizeof(vis));
    memset(cnt,0,sizeof(cnt));
    memset(dis,-1,sizeof(dis));
    dis[src]=0;
    cnt[src]++;
    queue<int>Q;
    Q.push(src);
    vis[src]=true;
    while(!Q.empty()){
        int u=Q.front();
        Q.pop();
        vis[u]=false;
        for(int i=u+1;i<=n+1;i++){
            if(g[u][i]!=-1){
                if(dis[i]<dis[u]+g[u][i]){
                    dis[i]=dis[u]+g[u][i];
                    path[i]=u;
                    if(!vis[i]){
                        Q.push(i);
                        cnt[i]++;
                        if(cnt[i]>n+1)return false;
                    }
                }
            }
        }

    }
    return true;
}

最长路

最长路问题有两种解决方法，一种是将边权取反，然后求最短路，或者直接改一下上述模板，一般选择后者，不排除有特殊情况，不过最长路也要小心有环的情况。

经典例题

P1339 [USACO09OCT]热浪Heat Wave

P1462 通往奥格瑞玛的道路

P1346 电车

P1119 灾后重建

P1144 最短路计数

P1522 牛的旅行 Cow Tours