四元数插值与均值（姿态平滑）

 

四元数插值与均值（姿态平滑）

• 四元数的求负是对每个分量变负就可以了，即q=(w,x,y,z)q=(w,x,y,z)，−q=(−w,−x,−y,−z)−q=(−w,−x,−y,−z)。但是q和-q表示的角位移是相同的，当旋转角为360°或其整数倍时，不会改变q的角位移，但是q的四个分量都变负了
• 四元数与标量相乘：kq=k[w,x,y,z]=[kw,kx,ky,kz]kq=k[w,x,y,z]=[kw,kx,ky,kz]
• 四元数的点乘:q1⋅q2=[w1v1]⋅[w2v2]=w1w2+v1⋅v2=w1w2+x1x2+y1y2+z1z2q1⋅q2=[w1v1]⋅[w2v2]=w1w2+v1⋅v2=w1w2+x1x2+y1y2+z1z2。四元数点乘的绝对值越大，代表其方向越相近。
• 四元数乘法（叉乘）：p=t+v⃗ p=t+v→、q=a+u⃗ q=a+u→，则pq=at−u⃗ ⋅v⃗ +av⃗ +tu⃗ +u⃗ ×v⃗ pq=at−u→⋅v→+av→+tu→+u→×v→
• 四元数的模长（范数）：∥q∥=x2+y2+z2+w2−−−−−−−−−−−−−−√=q⋅q∗−−−−−√‖q‖=x2+y2+z2+w2=q⋅q∗
• 四元数的共轭：四元数的共轭就是让四元数的向量部分取负，即若q=(w,x,y,z)q=(w,x,y,z)，则其共轭为q∗=(w,−x,−y,−z)q∗=(w,−x,−y,−z)
• 四元数的逆：由于qq∗=∥q∥2qq∗=‖q‖2，因此qq∗∥q∥2=1qq∗‖q‖2=1。若四元数存在逆q−1q−1，则qq−1=q−1q=1qq−1=q−1q=1，因此当∥q∥≠0‖q‖≠0时：

  q−1=q∗∥q∥2q−1=q∗‖q‖2

  对于单位四元数来说有q−1=q∗q−1=q∗
• 用四元数旋转矢量：对于矢量v⃗ =(x,y,z)v→=(x,y,z)，给定一个单位四元数q，让v⃗ v→旋转q。首先将v⃗ v→改写成四元素的形式v = (0, x, y ,z)，接下来进行如下变换：

  v′=qvq−1v′=qvq−1

   

---

•  四元数的球面线性插值（Slerp）

　　对于一般线性插值来说：r=P0+(P1−P0)tr=P0+(P1−P0)t，其中t∈[0, 1]，代表了插值矢量r末端在弦P0-P1上的位置。假如t取值为1/4、2/4、3/4即将P0P1弦长均分为4等份，可以看出其对应的弧长并不相等。靠近中间位置的弧长较长，而靠近两段处的弧长较短，这就意味着当t匀速变化时，代表姿态矢量的角速度变化并不均匀：　　To better solve the nonconstant rotation speed and normalization issues, we need an interpolation method known as spherical linear interpolation (usually abbreviated as slerp). Slerp is similar to linear interpolation except that instead of interpolating along a line, we’re interpolating along an arc on the surface of a sphere. Figure 10.21 shows the desired result. When using spherical interpolation at quarter intervals of t, we travel one-quarter of the arc length to get from orientation to orientation. We can also think of slerp as interpolating along the angle, or in this case, dividing the angle between the orientations into quarter intervals. 

　球面线性插值（Spherical linear interpolation，通常简称Slerp），是四元数的一种线性插值运算，主要用于在两个表示旋转的四元数之间平滑差值。下面来简单推导一下Slerp的公式。插值的一般公式可以写为：r=a(t)p+b(t)qr=a(t)p+b(t)q，现在要找到合适的a(t)和b(t)。注意单位向量p和q之间的夹角为θ，p和r之间的夹角为tθ，q和r之间的夹角为(1-t)θ：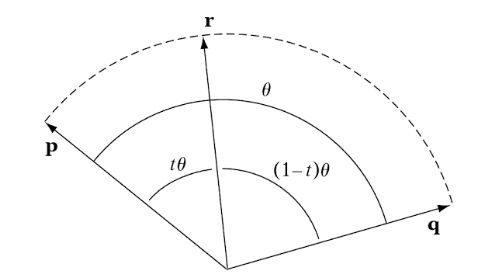

　　将上面的公式两边点乘p可得

p⋅rcostθ=a(t)p⋅p+b(t)p⋅q=a(t)+b(t)cosθp⋅r=a(t)p⋅p+b(t)p⋅qcos⁡tθ=a(t)+b(t)cos⁡θ

　　同样地，对公式两边点乘q可得

cos[(1−t)θ]=a(t)cosθ+b(t)cos⁡[(1−t)θ]=a(t)cos⁡θ+b(t)

　　两个方程可以解出两个未知量a(t)和b(t)：

a(t)b(t)=costθ−cos[(1−t)θ]cosθ1−cos2θ=cos[(1−t)θ]−costθcosθ1−cos2θa(t)=cos⁡tθ−cos⁡[(1−t)θ]cos⁡θ1−cos2⁡θb(t)=cos⁡[(1−t)θ]−cos⁡tθcos⁡θ1−cos2⁡θ

 　　使用三角函数公式可以将其化简为：

a(t)b(t)=sin[(1−t)θ]sinθ=sintθsinθa(t)=sin⁡[(1−t)θ]sin⁡θb(t)=sin⁡tθsin⁡θ

 　　于是四元数的球面线性插值公式为：

Slerp(p,q,t)=sin[(1−t)θ]p+sintθqsinθSlerp(p,q,t)=sin⁡[(1−t)θ]p+sin⁡tθqsin⁡θ

　　注意这个公式有2个问题，必须在实现过程中加以考虑：

• 如果四元数点积的结果是负值（夹角大于90°），那么后面的插值就会在4D球面上绕远路。为了解决这个问题，先测试点积的结果，当结果是负值时，将2个四元数的其中一个取反（并不会改变它代表的朝向）。而经过这一步操作，可以保证这个旋转走的是最短路径。

• 当p和q的夹角θ差非常小时会导致sinθ→0，这时除法可能会出现问题。为了避免这样的问题，当θ非常小时可以使用简单的线性插值代替（θ→0时，sinθ≈θ，因此方程退化为线性方程：slerp(p,q,t)=(1-t)p+tq）

 　　具体实现可以参考下面的代码：

 

#include 
#include 

void slerp(float starting[4], float ending[4], float result[4], float t )
{
    float cosa = starting[0]*ending[0] + starting[1]*ending[1] + starting[2]*ending[2] + starting[3]*ending[3];
    
    // If the dot product is negative, the quaternions have opposite handed-ness and slerp won't take
    // the shorter path. Fix by reversing one quaternion.
    if ( cosa < 0.0f ) 
    {
        ending[0] = -ending[0];
        ending[1] = -ending[1];
        ending[2] = -ending[2];
        ending[3] = -ending[3];
        cosa = -cosa;
    }
    
    float k0, k1;
    
    // If the inputs are too close for comfort, linearly interpolate
    if ( cosa > 0.9995f ) 
    {
        k0 = 1.0f - t;
        k1 = t;
    }
    else 
    {
        float sina = sqrt( 1.0f - cosa*cosa );
        float a = atan2( sina, cosa );
        k0 = sin((1.0f - t)*a)  / sina;
        k1 = sin(t*a) / sina;
    }
    result[0] = starting[0]*k0 + ending[0]*k1;
    result[1] = starting[1]*k0 + ending[1]*k1;
    result[2] = starting[2]*k0 + ending[2]*k1;
    result[3] = starting[3]*k0 + ending[3]*k1;
}



int main()
{
     
    float p[4] = {1,0,0,0};
    float q[4] = {0.707,0,0,0.707};
    float r[4] = {0};

    slerp(p,q,r,0.333);
    std::cout<

View Code

 　　下图中，X轴指向代表的姿态四元数为(1,0,0,0)，Y轴指向代表的姿态四元数为(0.707,0,0,0.707)，转换为Z-Y-X欧拉角为(0,0,90°)，即Y轴由X轴绕Z轴旋转90°得到。那么对这两个姿态进行插值，将其三等分（分别绕Z轴旋转30°和60°），根据欧拉角转四元数的公式得到r1=(0.966,0,0,0.259)，r2=(0.866,0,0,0.5)

　　上面代码输出的插值结果如下，可以看出与理论分析一致：

 

---

• 四元数的平均值

 　　Kinect获取到的人体关节姿态数据的噪声比较大，如果直接用这些原始的四元数去控制模型会造成模型抖动，于是想到对四元数求均值来进行平滑滤波。对n个四元数q1、q2、...qn求其加权平均值（权值分别为w1、w2、...wn），如果采用下面这种最直观的公式会出现一些问题

q¯bad=(∑i=1nwi)−1∑i=1nwiqiq¯bad=(∑i=1nwi)−1∑i=1nwiqi

　　比如对于四元数q和-q代表同一姿态，因此对于上面方程中任一qi改变其符号不应影响均值，但显然上面的公式并不具备这一性质。于是有人提出了其他方法来计算多个四元数之间的加权平均值：

　　Equations 12 and 13 in Markley et al.'s paper "Quaternion Averaging" (2007) define the weighted average of n quaterions qi with scalar weights wi：

q¯=argmaxq∈S3qTMqq¯=argmaxq∈S3qTMq

where

M=∑i=1nwiqiqTiM=∑i=1nwiqiqiT

　　That is, interpret the quaternions as vectors in R4R4, form the matrix M, and take its largest eigenvector. 即根据四元数和其对应的权值构造4×4矩阵M，M最大特征值对应的单位特征向量就是要求的加权平均值。

 　　根据论文，求四元数加权平均值的MATLAB程序如下：

% Q is an Nx4 matrix of quaternions. weights is an Nx1 vector, a weight for each quaternion.
% Qavg is the weightedaverage quaternion

% Markley, F. Landis, Yang Cheng, John Lucas Crassidis, and Yaakov Oshman. 
% "Averaging quaternions." Journal of Guidance, Control, and Dynamics 30, 
% no. 4 (2007): 1193-1197.

function [Qavg] = quatWAvgMarkley(Q, weights)

% Form the symmetric accumulator matrix
M = zeros(4, 4);
n = size(Q, 1);   % amount of quaternions
wSum = 0;

for i = 1:n
    q = Q(i,:)';
    w_i = weights(i);
    M = M + w_i.*(q*q');
    wSum = wSum + w_i;
end

% scale
M = (1.0/wSum)*M;

% The average quaternion is the eigenvector of M corresponding to the maximum eigenvalue. 
% Get the eigenvector corresponding to largest eigen value
[Qavg, ~] = eigs(M, 1);

end

　　下面测试一组数据，6个姿态分别表示绕Z轴旋转一定角度，求其平均姿态：

>> Q = [1,0,0,0; 0.999,0,0,0.044; 0.999,0,0,0.035; 1,0,0,0.026; 1,0,0,0.017; 1,0,0,0.009]  % 0°,5°,4°,3°,2°,1° rotation about Z-axis
>> w = ones(6,1) / 6
>> quatWAvgMarkley(Q, w)

　　输出结果为(-0.9998, 0, 0, -0.0218)，代表的平均姿态为绕Z轴旋转2.498°

　　求矩阵特征值和特征向量有很多快速的实现方式，不过计算量依然比较大。而当要求均值的四元数之间比较接近时还是可以采用简化的算法，经比较判断后直接求4个分量的均值。 Unity3D论坛中给出了这种简化算法的代码。Note: this code will only work if the separate quaternions are relatively close to each other.

//Get an average (mean) from more then two quaternions (with two, slerp would be used).
//Note: this only works if all the quaternions are relatively close together.
//Usage: 
//-Cumulative is an external Vector4 which holds all the added x y z and w components.
//-newRotation is the next rotation to be added to the average pool
//-firstRotation is the first quaternion of the array to be averaged
//-addAmount holds the total amount of quaternions which are currently added
//This function returns the current average quaternion
public static Quaternion AverageQuaternion(ref Vector4 cumulative, Quaternion newRotation, Quaternion firstRotation, int addAmount){
 
    float w = 0.0f;
    float x = 0.0f;
    float y = 0.0f;
    float z = 0.0f;
 
    //Before we add the new rotation to the average (mean), we have to check whether the quaternion has to be inverted. Because
    //q and -q are the same rotation, but cannot be averaged, we have to make sure they are all the same.
    if(!Math3d.AreQuaternionsClose(newRotation, firstRotation)){
 
        newRotation = Math3d.InverseSignQuaternion(newRotation);    
    }
 
    //Average the values
    float addDet = 1f/(float)addAmount;
    cumulative.w += newRotation.w;
    w = cumulative.w * addDet;
    cumulative.x += newRotation.x;
    x = cumulative.x * addDet;
    cumulative.y += newRotation.y;
    y = cumulative.y * addDet;
    cumulative.z += newRotation.z;
    z = cumulative.z * addDet;        
 
    //note: if speed is an issue, you can skip the normalization step
    return NormalizeQuaternion(x, y, z, w);
}
 
public static Quaternion NormalizeQuaternion(float x, float y, float z, float w){
 
    float lengthD = 1.0f / (w*w + x*x + y*y + z*z);
    w *= lengthD;
    x *= lengthD;
    y *= lengthD;
    z *= lengthD;
 
    return new Quaternion(x, y, z, w);
}
 
//Changes the sign of the quaternion components. This is not the same as the inverse.
public static Quaternion InverseSignQuaternion(Quaternion q){
 
    return new Quaternion(-q.x, -q.y, -q.z, -q.w);
}
 
//Returns true if the two input quaternions are close to each other. This can
//be used to check whether or not one of two quaternions which are supposed to
//be very similar but has its component signs reversed (q has the same rotation as
//-q)
public static bool AreQuaternionsClose(Quaternion q1, Quaternion q2){
 
    float dot = Quaternion.Dot(q1, q2);
 
    if(dot < 0.0f){
 
        return false;                    
    }
 
    else{
 
        return true;
    }
}

 

 

参考：

Rotations

Averaging Quaternions and Vectors

Maths - Quaternion Interpolation (SLERP)

Joint Orientation Smoothing [Unity C#]

“Average” of multiple quaternions?

Exchanging data between MATLAB and VREP

How would I apply an Exponential Moving Average to Quaternions?