FCN中反卷积、上采样、双线性插值之间的关系

未完待续。。。。。。

　　最近看很多人在群里问关于FCN中反卷积，上采样和双线性插值之间的关系，想着有必要整理下思路总结下，欢迎拍砖指正，也欢迎大家一同更新！

---

先看几个概念：
1、图像上采样
上采样upsampling的主要目的是放大图像，几乎都是采用内插值法，即在原有图像像素的基础上，在像素点值之间采用合适的插值算法插入新的元素。

2、线性插值法(linear interpolation)
　　这里讲解线性插值法的推导为了给双线性插值公式做铺垫。
　　线性插值法是指使用连接两个已知量的直线来确定在这个两个已知量之间的一个未知量的值的方法。
　　假设已知两个坐标 (x0,y0) 和 (x1,y1) ，要得到 [x0,x1] 区间内某一位置x在直线上的值。

　　该直线的方程可表示为： y−y0y1−y0=x−x0x1−x0
　　假设方程两边的值为α，那么这个值就是插值系数——从 x0 到 x 的距离与从 x0 到 x1 的距离的比值。由于x已知，所以可以从公式中得到α的值:
　　 α=y−y0y1−y0=x−x0x1−x0
这样
　　 y=(1−α)y0+αy1 =(1−x−x0x1−x0)y0+x−x0x1−x0y1

　　 =x1−xx1−x0y0+x−x0x1−x0y1 =x1−xx1−x0f(x1)+x−x0x1−x0f(x0)
　　
也就是：
　　 y=x1−xx1−x0f(x1)+x−x0x1−x0f(x0)

３、双线性插值
　　双线性插值是插值算法中的一种，是线性插值的扩展。利用原图像中目标点四周的四个真实存在的像素值来共同决定目标图中的一个像素值，其核心思想是在两个方向分别进行一次线性插值。

　　已知的红色数据点和待插值的绿色数据点
　　假如我们想得到未知函数f在点P= (x,y) 的值，假设我们已知函数f在 Q11=(x1,y1)、Q12=(x1,y2),Q21=(x2,y1)以及Q22=(x2,y2) 四个点 值。
　　第一步：X方向的线性插值，在Q12,Q22中插入蓝色点R2，Q11，Q21中插入蓝色点R1；
　　 f(R1)=x2−xx2−x1f(Q11)+x−x1x2−x1f(Q21)
　　
　　 f(R2)=x2−xx2−x1f(Q12)+x−x1x2−x1f(Q22)
　　第二步 ：Y方向的线性插值 ,通过第一步计算出的R1与R2在y方向上插值计算出P点。
　　 f(P)=y2−yy2−y1f(R1)+y−y1y2−y1f(R2)
　　在x与y方向上，z值成单调性特性的应用中，此种方法可以做外插运算，即可以求解Q11~Q22所构成的正方形以外的点的值。
　　
总结：线性插值法利用原图像中两个点计算像素值进行插值，双线性插值法利用原图像中四个点计算目标像素值进行插值。

---

3、FCN中的反卷积DeConvolution
　　使用反卷积将上一层的feature map放大，并使其输出在crop layer中进行切割，使其与ground truth具有相同的尺寸来计算每个像素点的误差。在作者的原文中提到deconvolutional layer中的kernel是可以被训练的，也可以是固定的，即默认的二维bilinear kernel。

　　之所以说FCN中的反卷积操作不是原则意义上transposed convolution，是因为作者设置其中的学习率lr_mult为0，没有让该层学习。即卷积核是固定不变的。
下列为train.prototxt关于DeConv层的代码：

layer {
  name: "upscore"
  type: "Deconvolution"
  bottom: "score_fr"
  top: "upscore"
  param {
    lr_mult: 0
  }
  convolution_param {
    num_output: 21
    bias_term: false
    kernel_size: 64
    stride: 32
  }
}

4、tranposed convolution

先看下卷积运算与矩阵运算之间的关系：
考虑如下一个简单的卷积层运算，其参数为：i=4,k=3,s=1,p=0，根据卷积运算得：o=2

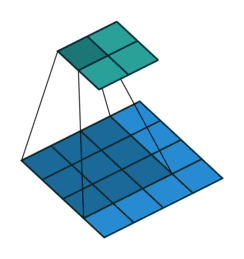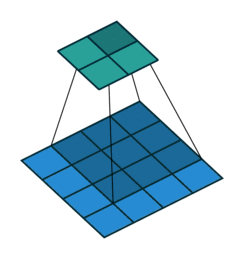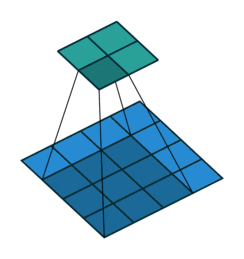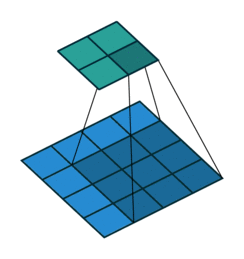
对于上述卷积运算，原图为X，我们把上图所示的3×3卷积核重叠划分为如下所示的[4,16]的稀疏矩阵 ,以行为主，每一行的元素为：卷积核每在一个位置时，与X进行成绩的核值（未覆盖到的位置为0）：
⎛⎝⎜⎜⎜⎜w0,0000w0,1w0,000w0,2w0,1000w0,200w1,00w0,00w1,1w1,0w0,1w0,0w1,2w1,1w0,2w0,10w1,20w0,2w2,00w1,00w2,1w2,0w1,1w1,0w2,2w2,1w1,2w1,10w2,20w1,200w2,0000w2,1w2,000w2,2w2,1000w2,2⎞⎠⎟⎟⎟⎟
未完待续。。。。。
参考博文：http://blog.csdn.net/kekong0713/article/details/68941498
知乎：https://www.zhihu.com/question/50349594