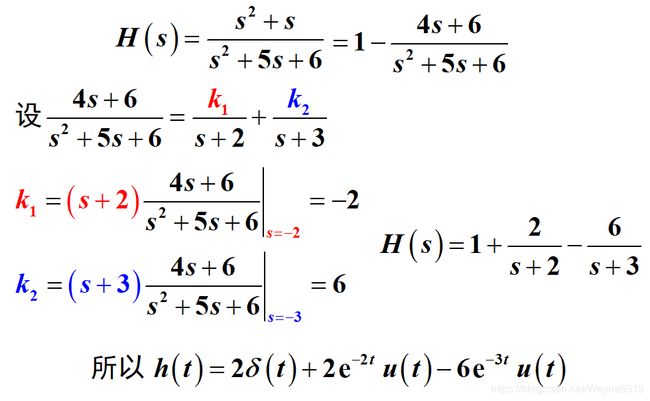s域等效电路与系统函数的引出
拉普拉斯变换分析动态电路
主要思路:将时域的电路图转换为 s s s域电路图,列写代数方程;
如果没有给出电路,只给出时移微分方程,则将微分方程中的每一项进行拉氏变换转换到 s s s域。
电路的 s s s域等效模型
电源
{ − E , t < 0 E , t > 0 \left\{\begin{aligned}-E, t<0\\E,t>0\end{aligned}\right. {−E,t<0E,t>0
两边取拉氏变换 E ( s ) = E s \bm{E(s)=\frac{E}{s}} E(s)=sE
无记忆性元件(电阻、导纳)
 或写成
或写成
由 i R ( t ) = v R ( t ) R \bm{i_R(t)=\frac{v_R(t)}{R}} iR(t)=RvR(t) 得 I R ( s ) = 1 R V R ( s ) \bm{I_R(s)=\frac{1}{R}V_R(s)} IR(s)=R1VR(s)
记忆性储能元件(电容、电感)
根据时域微分性质:
L [ f ′ ( t ) ] = s F ( s ) − f ( 0 − ) \bm{\mathscr{L}[f^{'}(t)]=sF(s)-f(0_{-})} L[f′(t)]=sF(s)−f(0−)
L [ f ( 2 ) ( t ) ] = s 2 F ( s ) − s f ( 0 − ) − f ′ ( 0 − ) \bm{\mathscr{L}[f^{(2)}(t)]=s^2F(s)-sf(0_{-})-f^{'}(0_{-})} L[f(2)(t)]=s2F(s)−sf(0−)−f′(0−)
L [ f ( 3 ) ( t ) ] = s 3 F ( s ) − s 2 f ( 0 − ) − s f ′ ( 0 − ) − f ′ ′ ( 0 − ) \bm{\mathscr{L}[f^{(3)}(t)]=s^3F(s)-s^{2}f(0_{-})-sf^{'}(0_{-})-f^{''}(0_{-})} L[f(3)(t)]=s3F(s)−s2f(0−)−sf′(0−)−f′′(0−)

等效为 S S S域中的一个感抗为 L s Ls Ls的电感与原始储能为 L i L ( 0 − ) Li_L(0_{-}) LiL(0−)的电压源串联。
亦可根据单边拉氏变换积分性质:
L [ ∫ 0 t f ( t ) d t ] = F ( s ) s + f ′ ( 0 − ) s \bm{\mathscr{L}[\int_0^t f(t)dt]=\frac{F(s)}{s}+\frac{f^{'}(0_{-})}{s}} L[∫0tf(t)dt]=sF(s)+sf′(0−)
L [ ∫ 0 t ⋅ ⋅ ⋅ ∫ 0 t f ( t ) d t ] = F ( s ) s n \bm{\mathscr{L}[\int_0^t···\int_0^t f(t)dt]=\frac{F(s)}{s^n}} L[∫0t⋅⋅⋅∫0tf(t)dt]=snF(s)
等效为 S S S域中的一个感抗为 L s Ls Ls的电感与原始储能为 i L ( 0 − ) s \bm{\frac{i_L(0_{-})}{s}} siL(0−)的电流源并联。
即 I L ( s ) = V L ( s ) s L + i L ( 0 − ) s \bm{I_{L}(s)=\frac{V_{L}(s)}{sL}+\frac{i_L(0_{-})}{s}} IL(s)=sLVL(s)+siL(0−)


亦可根据微分性质,由 i C ( t ) = C d v C ( t ) d t 得 I C ( s ) = C s V C ( s ) − C v C ( 0 − ) \bm{i_C(t)=C\frac{dv_C(t)}{dt} 得 I_C(s)=CsV_C(s)-Cv_C(0_{-})} iC(t)=CdtdvC(t)得IC(s)=CsVC(s)−CvC(0−)
即也有电压源串联和电流源并联两种等效模型。
系统函数
在零状态响应的条件下,s域模型可以得到简化,网络任意端口激励信号的拉氏变换与任意端口响应信号的拉氏变换之比仅有网络元件的阻抗、导纳特性决定,可用系统函数(或网络函数)来描述这一特性。
系统函数 H ( s ) = 零 状 态 响 应 的 拉 氏 变 换 激 励 的 拉 氏 变 换 = R ( s ) E ( s ) \bm{H(s)=\frac{零状态响应的拉氏变换}{激励的拉氏变换}=\frac{R(s)}{E(s)}} H(s)=激励的拉氏变换零状态响应的拉氏变换=E(s)R(s)
激励、零状态响应、冲激响应分别为 e ( t ) 、 r ( t ) 、 h ( t ) e(t)、r(t)、h(t) e(t)、r(t)、h(t)
时域分析中, r ( t ) = h ( t ) ∗ e ( t ) \bm{r(t) = h(t) * e(t)} r(t)=h(t)∗e(t)
由卷积定理得 s 域 s域 s域分析中, R ( s ) = H ( s ) ⋅ E ( s ) \bm{R(s) = H(s)·E(s)} R(s)=H(s)⋅E(s)
H ( s ) = R ( s ) E ( s ) = L [ h ( t ) ] \bm{H(s)=\frac{R(s)}{E(s)}=\mathscr{L}[h(t)]} H(s)=E(s)R(s)=L[h(t)],冲激响应 h ( t ) h(t) h(t)与系统函数 H ( s ) H(s) H(s)构成变换对。
运用系统函数求解的方便之处就在于零状态下初始条件项都为0
对微分方程两边取双边拉氏变换