前面的文章实现了无向图深度优先搜索和广度优先搜索解决了无向图中的路径寻找,不过无向图中还有几个比较常见的问题需要解决,判断图中的连通分量,在无向图中,如果从顶点vi到顶点vj有路径,则称vi和vj连通。如果图中任意两个顶点之间都连通,则称该图为连通图,否则,称该图为非连通图,则其中的极大连通子图称为连通分量,这里所谓的极大是指子图中包含的顶点个数极大。
连通分量
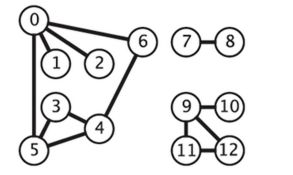
为了编程和理解,我们还是使用之前文章的非连通图,如下图所示,图中有三个连通分量,看着这个图对照上文中的概念比较好理解:
代码中跟深度优先搜索有所改动,需要一个新的数组存储对应的值,数组中0-6都属于一个连通分量,那么我们可以将数组中索引在0-6之间的变量赋值为0,代码如下:
@interface GraphCC : NSObject
//记录顶点是否被标记
@property (strong,nonatomic) NSMutableArray *marked;
@property (assign,nonatomic) NSInteger count;//连通的分量
@property (strong,nonatomic) NSMutableArray *ids;//顶点所在的连通分量的标识符
//连通分量递归初始化
-(instancetype)initWithGraph:(Graph *)graph;
-(void)depthSearch:(Graph *)graph vertex:(NSInteger)vertex;
@end
实现代码如下:
@implementation GraphCC
#pragma mark getter and setter
-(NSMutableArray *)marked{
if (!_marked) {
_marked=[[NSMutableArray alloc]initWithCapacity:1];
}
return _marked;
}
-(NSMutableArray *)ids{
if (!_ids) {
_ids=[[NSMutableArray alloc]initWithCapacity:1];
}
return _ids;
}
-(instancetype)initWithGraph:(Graph *)graph{
self=[super init];
if (self) {
for (NSInteger i=0; i测试代码:
Graph *graph=[[Graph alloc]initWithVertex:13];
[graph addEdges:0 endVertex:1];
[graph addEdges:0 endVertex:2];
[graph addEdges:0 endVertex:5];
[graph addEdges:0 endVertex:6];
[graph addEdges:3 endVertex:4];
[graph addEdges:3 endVertex:5];
[graph addEdges:4 endVertex:5];
[graph addEdges:4 endVertex:6];
[graph addEdges:7 endVertex:8];
[graph addEdges:9 endVertex:10];
[graph addEdges:9 endVertex:11];
[graph addEdges:9 endVertex:12];
[graph addEdges:11 endVertex:12];
GraphCC *graphCC=[[GraphCC alloc]initWithGraph:graph];
for (NSInteger i=0; i效果如下:
是否有环
环简单就是几个顶点之间是否存在闭合,从顶点1通过若干个顶点是否可以返回到顶点1,此次判断通过之前文章的一个连通图:
@interface GraphCycle : NSObject
//记录顶点是否被标记
@property (strong,nonatomic) NSMutableArray *marked;
@property (assign,nonatomic) Boolean hasCycle;
//初始化
-(instancetype)initWithGraph:(Graph *)graph;
-(void)depthSearch:(Graph *)graph vertex:(NSInteger)vertex nextVertex:(NSInteger)nextVertex;
@end
实现代码:
@implementation GraphCycle
#pragma mark getter and setter
-(NSMutableArray *)marked{
if (!_marked) {
_marked=[[NSMutableArray alloc]initWithCapacity:1];
}
return _marked;
}
-(instancetype)initWithGraph:(Graph *)graph{
self=[super init];
if (self) {
for (NSInteger i=0; i测试代码:
Graph *graph=[[Graph alloc]initWithVertex:6];
[graph addEdges:0 endVertex:5];
[graph addEdges:2 endVertex:4];
[graph addEdges:2 endVertex:3];
[graph addEdges:1 endVertex:2];
[graph addEdges:0 endVertex:1];
[graph addEdges:3 endVertex:4];
[graph addEdges:5 endVertex:3];
[graph addEdges:0 endVertex:2];
GraphCycle *cycle=[[GraphCycle alloc]initWithGraph:graph];
if ([cycle hasCycle]) {
NSLog(@"图中含有环");
}else{
NSLog(@"图中不含有环");
}
NSLog(@"技术交流群:%@",@"228407086");
NSLog(@"原文地址:http://www.cnblogs.com/xiaofeixiang");
测试效果:
二分图
我们也许会看到过这么一个问题就是是否能够用两种颜色将图中的所有顶点着色,,使得任意一条边的两个点都不相同,其实这个问题等价于图是否是二分图:
@interface GraphTwoColor : NSObject
//标记数组
@property (strong,nonatomic) NSMutableArray *marked;
@property (strong,nonatomic) NSMutableArray *color;
@property (assign,nonatomic) Boolean isTwoColorable;
//初始化
-(instancetype)initWithGraph:(Graph *)graph;
//深度搜索
-(void)depthSearch:(Graph *)graph vertex:(NSInteger)vertex;
@end实现代码:
@implementation GraphTwoColor
#pragma mark getter and setter
-(NSMutableArray *)marked{
if (!_marked) {
_marked=[[NSMutableArray alloc]initWithCapacity:1];
}
return _marked;
}
-(NSMutableArray *)color{
if (!_color) {
_color=[[NSMutableArray alloc]initWithCapacity:1];
}
return _color;
}
-(instancetype)initWithGraph:(Graph *)graph{
self=[super init];
if (self) {
for (NSInteger i=0; i测试代码:
Graph *graph=[[Graph alloc]initWithVertex:6];
[graph addEdges:0 endVertex:5];
[graph addEdges:2 endVertex:4];
[graph addEdges:2 endVertex:3];
[graph addEdges:1 endVertex:2];
[graph addEdges:0 endVertex:1];
[graph addEdges:3 endVertex:4];
[graph addEdges:5 endVertex:3];
[graph addEdges:0 endVertex:2];
GraphTwoColor *graphColor=[[GraphTwoColor alloc]initWithGraph:graph];
if ([graphColor isTwoColorable]) {
NSLog(@"图是一个二分图");
}else{
NSLog(@"图不是一个二分图");
}
NSLog(@"技术交流群:%@",@"228407086");
NSLog(@"原文地址:http://www.cnblogs.com/xiaofeixiang");
测试效果:
如果我们修改一下Graph,比如图只有四个顶点,四条边,肯定是一个二分图:
Graph *graph=[[Graph alloc]initWithVertex:4];
[graph addEdges:0 endVertex:1];
[graph addEdges:0 endVertex:2];
[graph addEdges:1 endVertex:3];
[graph addEdges:2 endVertex:3];