二分匹配和一般图匹配

二分匹配

匈牙利算法

例题

不说过程了，也没有动图。。。

因为只是一个比较潦草的学习笔记。

首先，我们找到一个公牛，去找一个母牛，如果她没匹配，就匹配，匹配了，就让她匹配了，就让她的公牛找別的找到了，就可以多算一对了。

当然，这样会超时，为何

虚线为未匹配边，实线为匹配边，这张图会陷入无限死循环。

因此我们要标记这个母牛在这次DFS有没有找过。

而且这样还有个好处，找过的母牛就算其他公牛再找她，最后也是找不到的，毕竟原本我找她都没有，你找她就会有了？

代码：

#include
#include
#include
using  namespace  std;
int  match[210000],n,m,k,ans;
bool  chw[210000];
struct  node
{
	int  y,next;
}a[210000];int  len,last[210000];
void  ins(int  x,int  y)
{
	len++;
	a[len].y=y;a[len].next=last[x];last[x]=len;
}
bool  findmu(int  x)
{
	for(int  k=last[x];k;k=a[k].next)
	{
		int  y=a[k].y;
		if(chw[y]==true)
		{
			chw[y]=false;//防止超时的
			if(match[y]==0  ||  findmu(match[y])==true)
			{
				match[y]=x;
				return  true;
			}
		}
	}
	return  false;
}
int  main()
{
	scanf("%d%d%d",&n,&m,&k);
	for(int  i=1;i<=k;i++)
	{
		int  x,y;scanf("%d%d",&x,&y);
		ins(x,y);
	}
	for(int  i=1;i<=n;i++)
	{
		memset(chw,true,sizeof(chw));//每头母牛还没找
		if(findmu(i)==true)ans++;
	}
	printf("%d\n",ans);
	return  0;
}

练习

1

1

我们可以把课程与日期相连边，再跑二分匹配。

#include
#include
using  namespace  std;
struct  node
{
	int  x1,x2,y,next;
}a[210000];int  len=0,last[10][20];
struct  muniu
{
	int  q,p;
	muniu()
	{
		q=0;p=0;
	}
}match[501];
int  n,tt=0,chw[501];
void  ins(int  x,int  y,int  z)
{
	len++;
	a[len].x1=x;a[len].x2=y;a[len].y=z;
	a[len].next=last[x][y];last[x][y]=len;
}
bool  find_muniu(int  x,int  y)
{
	for(int  k=last[x][y];k>0;k=a[k].next)
	{
		int  z=a[k].y;
		if(chw[z]!=tt)
		{
			chw[z]=tt;
			if(match[z].q==0  ||  find_muniu(match[z].q,match[z].p)==true)
			{
				match[z].q=x;match[z].p=y;
				return  true;
			}
		}
	}
	return  false;
}
int  main()
{
	scanf("%d",&n);
	for(int  i=1;i<=n;i++)
	{
		int  m;scanf("%d",&m);
		for(int  j=1;j<=m;j++)
		{
			int  x,y;scanf("%d%d",&x,&y);
			ins(x,y,i);
		}
	}
	memset(chw,0,sizeof(chw));tt=0;
	int  s=0;
	for(int  i=1;i<=7;i++)
	{
		for(int  j=1;j<=12;j++)
		{
			tt++;
			if(find_muniu(i,j)==true)s++;
		}
	}
	printf("%d\n",s);
}

2

2

我们可以判断这个老鼠可不可以在规定时间跑到地洞里去，可以就连边。

#include
#include
#include
using  namespace  std;
struct  laoshu
{
	double  x,y;
}ls[110];
struct  didong
{
	double  x,y;
}dd[110];
struct  node
{
	int  x,y,next;
}a[210000];int  len,last[11000];
int  n,m,tt=0;
int  match[11000],chw[11000];
void  ins(int  x,int  y)
{
	len++;
	a[len].x=x;a[len].y=y;a[len].next=last[x];last[x]=len;
}
double  dis(laoshu  n1,didong  n2)
{
	return  sqrt((n2.x-n1.x)*(n2.x-n1.x)+(n2.y-n1.y)*(n2.y-n1.y));
}
bool  find_muniu(int  x)
{
	for(int  k=last[x];k>0;k=a[k].next)
	{
		int  y=a[k].y;
		if(chw[y]!=tt)
		{
			chw[y]=tt;
			if(match[y]==0  ||  find_muniu(match[y])==true)
			{
				match[y]=x;
				return  true;
			}
		}
	}
	return  false;
}
int  main()
{
	int  s,v;
	while(scanf("%d%d%d%d",&n,&m,&s,&v)!=EOF)
	{
		len=0;memset(last,0,sizeof(last));
		for(int  i=1;i<=n;i++)scanf("%lf%lf",&ls[i].x,&ls[i].y);
		for(int  i=1;i<=m;i++)scanf("%lf%lf",&dd[i].x,&dd[i].y);
		for(int  i=1;i<=n;i++)
		{
			for(int  j=1;j<=m;j++)
			{
				if(dis(ls[i],dd[j])<=s*v)
				{
					ins(i,j);
				}
			}
		}
		memset(match,0,sizeof(match));
		memset(chw,0,sizeof(chw));tt=0;
		int  ans=0;
		for(int  i=1;i<=n;i++)
		{
			tt++;
			if(find_muniu(i)==true)ans++;
		}
		printf("%d\n",n-ans);
	}
	return  0;
}

最小覆盖

例题

---

一下摘自http://caioj.cn/problem.php?id=1151

最少点覆盖所有边
中山市第一中学 沈楚炎

在oi和ACM比赛中，直接用最大二分匹配(匈牙利算法)解题的题目较少，往往披上一层“最小覆盖”的外衣，这类题目从表面看好像跟最大二分匹配无关，然而应用König定理可以轻松解决这类问题，本文给出König定理的证明，并且应用König定理展示解题中基本的构图技巧。

阅读本文需要读者先理解二分图的概念并且掌握匈牙利算法。

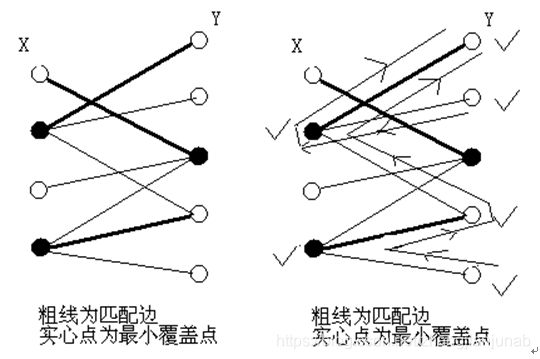
最小点覆盖数：在二分图中选了一个点(X集合或Y集合都行)就相当于覆盖了以它为端点的所有边，求覆盖所有边所需的最少点数。

König定理：一个二分图中的最大匹配数等于这个图中的最小点覆盖数。

在证明定理之前，让我们先用它来解决例题1。

König定理证明：

虽然直接应用König定理可以解决许多最小覆盖的题目，但这类题难点往往在于构图，要做到灵活构图应用König定理，则对其证明需要有一定的了解。König定理的证明是建立在匈牙利算法操作细节上的，掌握匈牙利算法的全过程很重要。
假设二分图G分为左边X和右边Y两个互不相交的点集。G经过匈牙利算法后找到一个最大匹配M，则可知G中再也找不到一条增广路径。

根据König定理从最大匹配边中选M个点。下来说明选点策略，再证明这个策略的正确性。

选点策略：

标记右边未匹配边的顶点，并从右边未匹配边的顶点出发，按照边：未匹配→匹配→未匹配→……的原则标记途中经过的顶点，则最后一条经过的边必定为匹配边(否则为增广路经)。重复上述过程，直到右边不再含有未匹配边的点。

记得到的左边已标记的点和右边未标记的点为S， 以下证明S即为所求的最小顶点集。

证明选点策略：

1、| S | 等于 M

左边标记的点全都为匹配边的顶点，右边未标记的点也为匹配边的顶点。因此，我们得到的点与匹配边一一对应。

2、S能覆盖G中所有的边。

根据左右端点是否被标记，G中所有的边有以下四种情况：

① 左右均标记；

② 左右均无标记；

③ 左边标记，右边未标记；

④ 左边未标记，右边标记；

前三种，S 中点(包含：左边的点(标记)+右边的点(未标记))都能得到的，除了④。下面证明④不存在。

假如存在一条边e不属于S所覆盖的边集，且e 左边未标记右边标记。

如果e不属于匹配边，那么左端点就可以通过这条边右端点到达（从而得到标记）；

如果e属于匹配边，那么右端点的标记从哪里来？它的标记只能是从这条匹配边的左端点过来，那么左端点就应该有标记。

3、S是最小的覆盖。

因为最大匹配M中，M条边两两之间没有共同交点，所以要覆盖这M条匹配边至少就需要M个点。

证毕。

总结：如果你真的超级无敌懒(严重不推荐)，那就记住以下结论(如果你理解了以上证明，也要背以下结论)：

1、要摧毁所有边，选“最大匹配数”个点。(做题建造模型的时候要着重思考什么当成边，什么当成点)

2、扩展，选最少的点消失，让X集合和Y集合失去联系 (提醒这个是为了以后网络流的最小割做点不知道会起什么作用的铺垫)

#include
#include
using  namespace  std;
struct  node
{
	int  x,y,next;
}a[210000];int  len=0,last[11000];
int  n,m,tt=0;
int  match[11000],chw[11000];
void  ins(int  x,int  y)
{
	len++;
	a[len].x=x;a[len].y=y;a[len].next=last[x];last[x]=len;
}
bool  find_muniu(int  x)
{
	for(int  k=last[x];k>0;k=a[k].next)
	{
		int  y=a[k].y;
		if(chw[y]!=tt)
		{
			chw[y]=tt;
			if(match[y]==0  ||  find_muniu(match[y])==true)
			{
				match[y]=x;
				return  true;
			}
		}
	}
	return  false;
}
int  main()
{
	int  k;scanf("%d%d%d",&n,&m,&k);
	for(int  i=1;i<=k;i++)
	{
		int  x,y;scanf("%d%d",&x,&y);
		ins(x,y);
	}
	memset(match,0,sizeof(match));
	memset(chw,0,sizeof(chw));tt=0;
	int  s=0;
	for(int  i=1;i<=n;i++)
	{
		tt++;
		if(find_muniu(i)==true)s++;
	}
	printf("%d\n",s);
}

练习

1

1

我们把每个地雷的行和列连接，跑一边最小覆盖

#include
#include
using  namespace  std;
struct  node
{
	int  x,y,next;
}a[210000];int  len=0,last[11000];
int  n,m,tt=0;
int  match[11000],chw[11000];
void  ins(int  x,int  y)
{
	len++;
	a[len].x=x;a[len].y=y;a[len].next=last[x];last[x]=len;
}
bool  find_muniu(int  x)
{
	for(int  k=last[x];k>0;k=a[k].next)
	{
		int  y=a[k].y;
		if(chw[y]!=tt)
		{
			chw[y]=tt;
			if(match[y]==0  ||  find_muniu(match[y])==true)
			{
				match[y]=x;
				return  true;
			}
		}
	}
	return  false;
}
int  main()
{
	scanf("%d%d",&n,&m);
	for(int  i=1;i<=m;i++)
	{
		int  x,y;scanf("%d%d",&x,&y);
		ins(x,y);
	}
	memset(match,0,sizeof(match));
	memset(chw,0,sizeof(chw));tt=0;
	int  s=0;
	for(int  i=1;i<=n;i++)
	{
		tt++;
		if(find_muniu(i)==true)s++;
	}
	printf("%d\n",s);
	return  0;
}

2

2

我们预处理出每个水在几号横向木板和纵向木板，连边。。。

#include
#include
#include
using  namespace  std;
int  match[210000],chw[210000],a[60][60],b[60][60],n,m,nn=1,mm=1,tt;
char  ss[60][60];
struct  node
{
	int  y,next;
}tr[210000];int  len,last[210000];
void  ins(int  x,int  y)
{
	len++;
	tr[len].y=y;tr[len].next=last[x];last[x]=len;
}
bool  find_muniu(int  x)
{
	for(int  k=last[x];k;k=tr[k].next)
	{
		int  y=tr[k].y;
		if(chw[y]!=tt)
		{
			chw[y]=tt;
			if(match[y]==0  ||  find_muniu(match[y])==true)
			{
				match[y]=x;
				return  true;
			}
		}
	}
	return  false;
}
int  main()
{
	scanf("%d%d",&n,&m);
	for(int  i=1;i<=n;i++)
	{
		scanf("%s",ss[i]+1);
		for(int  j=1;j<=m;j++)
		{
			if(ss[i][j]=='*')a[i][j]=nn;
			else  if(ss[i][j]=='.'  &&  ss[i][j-1]=='*')nn++;
		}
		if(ss[i][m]=='*')nn++;
	}
	for(int  i=1;i<=m;i++)
	{
		for(int  j=1;j<=n;j++)
		{
			if(ss[j][i]=='*')b[j][i]=mm;
			if(ss[j][i]=='.'  &&  ss[j-1][i]=='*')mm++;
		}
		if(ss[n][i]=='*')mm++;
	}
	for(int  i=1;i<=n;i++)
	{
		for(int  j=1;j<=m;j++)
		{
			if(ss[i][j]=='*')ins(a[i][j],b[i][j]);
		}
	}
	int  ans=0;
	for(int  i=1;i<=nn;i++)
	{
		tt++;
		if(find_muniu(i)==true)ans++;
	}
	printf("%d\n",ans);
	return  0;
}

二分图一般独立集

例题

一般独立集=点数-最小覆盖数。

#include
#include
using  namespace  std;
struct  node
{
	int  x,y,next;
}a[2100000];int  len=0,last[1100000];
long  long  n,m,tt=0;
long  long  match[1100000],chw[1100000];
void  ins(int  x,int  y)
{
	len++;
	a[len].x=x;a[len].y=y;a[len].next=last[x];last[x]=len;
}
bool  find_muniu(int  x)
{
	for(int  k=last[x];k>0;k=a[k].next)
	{
		int  y=a[k].y;
		if(chw[y]!=tt)
		{
			chw[y]=tt;
			if(match[y]==0  ||  find_muniu(match[y])==true)
			{
				match[y]=x;
				return  true;
			}
		}
	}
	return  false;
}
int  main()
{
	long  long  k;scanf("%lld%lld%lld",&n,&m,&k);
	for(int  i=1;i<=k;i++)
	{
		long  long  x,y;scanf("%lld%lld",&x,&y);
		ins(x,y);
	}
	memset(match,0,sizeof(match));
	memset(chw,0,sizeof(chw));tt=0;
	int  s=0;
	for(int  i=1;i<=n;i++)
	{
		tt++;
		if(find_muniu(i)==true)s++;
	}
	printf("%lld\n",n+m-s);
}

一般图

一般图的最大独立集。

这道题目是NP问题来的，我们容易知道：一般图的最大独立集=一般图补图的最大团

而最大团怎么做？

在这给大家推介两道题（放的都是https://vjudge.net/上的，容易上去）：

HDU-1530

POJ-2989

我们先讲最大团：

我们知道，我们是可以$O(2^n)$计算极大团（在一般图中不能再加入其他点的团）的数量的，也可以计算最大团（极大团中点数最多的团）点个数，但是$O(2^n)$你确定不会炸？

于是我们引进优美的暴力Bron-Kerbosch 算法

怎么做？

以极大团个数为例

首先，我们设立三个数组：some、all、none

all表示目前团中的点

some表示目前与all中所有点有边相连的点，也就是有可能成为团的点。

none表示这个点进过团后出来就进入none，可以理解为不能进入all里了，且none的点与all中所有点有边相连，作用是判重。

show time

1. 我们一开始把所有点踢进some里
2. 遍历some集合，然后把some里面的点加入团。
3. 将加入的点的临点与some和none做交集。
4. 做下一层循环，重复2过程
5. 循环结束，回复4过程前做的，且把目前加入的点踢入none里面
6. 如果some的点个数与none的点数为0，all中的就是极大团了。
7. 但是，如果some为0，而none不为0，这就不是极大团了，因为加入none的点不是会更大吗，但是这个团跟以前重复了。

pivot优化：
我们可以在some中选一个pivot点，如果我们选了pivot点，那么他的在some中的临点下次也会被选中，所以，pivot点的临点就不用再DFS了，而且我们可以按度数来排序，这样可以更好的利用pivot点。

POJ-2989
代码：

#include
#include
#include
using  namespace  std;
bool  maps[140][140];
int  some[140][140],all[140][140],none[140][140];
int  n,m,ans;
int  deg[140];
bool  cmp(int  x,int  y){return  deg[x]>deg[y];}//度数排序
void  BK(int  pos,int  al,int  so,int  no)
{
	if(so==0  &&  no==0)
	{
		ans++;
		return  ;
	}
	int  pi=0;//优化
	if(so)
	{
		pi=some[pos][1];
		for(int  i=1;i<=al;i++)all[pos+1][i]=all[pos][i];
	}
	for(int  i=1;i<=so;i++)
	{
		int  nxt=some[pos][i];
		if(maps[pi][nxt])continue;//优化
		int  nso=0,nno=0;
		all[pos+1][al+1]=nxt;
		for(int  j=1;j<=so;j++)
		{
			if(some[pos][j]!=-1  &&  maps[nxt][some[pos][j]])some[pos+1][++nso]=some[pos][j];
		}
		for(int  j=1;j<=no;j++)
		{
			if(maps[nxt][none[pos][j]])none[pos+1][++nno]=none[pos][j];
		}
		BK(pos+1,al+1,nso,nno);
		if(ans>1000)return  ;
		some[pos][i]=-1;none[pos][++no]=nxt;
	}
}
int  main()
{
	while(scanf("%d%d",&n,&m)!=EOF)
	{
		memset(maps,0,sizeof(maps));
		memset(deg,0,sizeof(deg));
		for(int  i=1;i<=n;i++)some[0][i]=i;
		for(int  i=1;i<=m;i++)
		{
			int  x,y;scanf("%d%d",&x,&y);
			maps[x][y]=maps[y][x]=true;
			deg[x]++;deg[y]++;
		}
		sort(some[0]+1,some[0]+n+1,cmp);
		ans=0;BK(0,0/*al*/,n/*so*/,0/*no*/);
		if(ans>1000)printf("Too many maximal sets of friends.\n");
		else  printf("%d\n",ans);
	}
	return  0;
}

极大团只需记录最大值：

POJ-2989

代码：

#include
#include
#include
using  namespace  std;
bool  maps[140][140];
int  some[140][140],all[140][140],none[140][140];
int  n,m,ans;
int  deg[140];
inline  bool  cmp(int  x,int  y){return  deg[x]>deg[y];}
void  BK(int  pos,int  al,int  so,int  no)
{
	if(al+so<=ans)return  ;
	if(so==0  &&  no==0)
	{
		ans=al;
		return  ;
	}
	int  pi=0;
	if(so)
	{
		pi=some[pos][1];
		for(int  i=1;i<=al;i++)all[pos+1][i]=all[pos][i];
	}
	for(int  i=1;i<=so;i++)
	{
		int  nxt=some[pos][i];
		if(maps[pi][nxt])continue;
		int  nso=0,nno=0;
		all[pos+1][al+1]=nxt;
		for(int  j=1;j<=so;j++)
		{
			if(maps[nxt][some[pos][j]])some[pos+1][++nso]=some[pos][j];
		}
		for(int  j=1;j<=no;j++)
		{
			if(maps[nxt][none[pos][j]])none[pos+1][++nno]=none[pos][j];
		}
		BK(pos+1,al+1,nso,nno);
		some[pos][i]=0;none[pos][++no]=nxt;
	}
}
int  main()
{
	while(scanf("%d",&n)!=EOF)
	{
		if(n==0)break;
		memset(maps,0,sizeof(maps));
		memset(deg,0,sizeof(deg));
		for(int  i=1;i<=n;i++)some[0][i]=i;
		for(int  i=1;i<=n;i++)
		{
			for(int  j=1;j<=n;j++)
			{
				int  x;scanf("%d",&x);
				if(x==1)maps[i][j]=true,deg[i]++;deg[j]++;
			}
		}
		sort(some[0]+1,some[0]+n+1,cmp);
		ans=0;BK(0,0/*al*/,n/*so*/,0/*no*/);
		printf("%d\n",ans);
	}
	return  0;
}

当然，大家发现了，在最大团中，all跟none都是没用的，而且极大团个数如果不用输出团的点也不用all。

于是我们可以试一试：

题目
代码：

#include
#include
#include
#define  N  410
#define  M  81000
using  namespace  std;
bool  maps[N][N];
int  some[N][N],dug[N];
int  n,m,ans;
inline  bool  cmp(int  x,int  y){return  dug[x]>dug[y];}
void  BK(int  pos,int  so,int  now)
{
	if(so+now<=ans)return  ;
	if(!so)
	{
		ans=now;return  ;
	}
	int  pi=some[pos][1];
	for(int  i=1;i<=so;i++)
	{
		int  nxt=some[pos][i];
		if(!maps[nxt][pi])continue;
		int  nso=0;
		for(int  j=1;j<=so;j++)
		{
			if(!maps[nxt][some[pos][j]])some[pos+1][++nso]=some[pos][j];
		}
		BK(pos+1,nso,now+1);
		some[pos][i]=0;
	}
}
int  main()
{
	scanf("%d%d",&n,&m);
	for(int  i=1;i<=n;i++)dug[i]=n-1,maps[i][i]=maps[0][i]=maps[i][0]=true,some[0][i]=i;
	for(int  i=1;i<=m;i++)
	{
		int  x,y;scanf("%d%d",&x,&y);
		dug[x]--;dug[y]--;maps[x][y]=maps[y][x]=true;
	}
	sort(some[0]+1,some[0]+n+1,cmp);
	ans=0;BK(0,n,0);
	printf("%d\n",ans);
	return  0;
}

真的可以优化！

至此，最大团完成

一般图匹配

带花树

带花树是一个致命的算法，很麻烦，但是我们可以逐步解析。

增广路

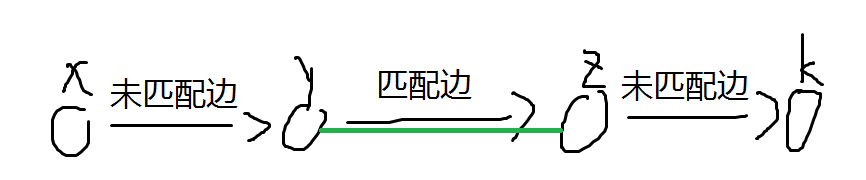
按照匈牙利算法，我们也可以找起点->未匹配边->匹配边->…->未匹配边（不能找到匹配边了）。
这条路径有什么好处？

原本，$match[y]=z,match[z]=y$，但是在这条增广路下，我们发现，我们可以把未匹配边变成匹配边，把匹配边变成未匹配边，而在增广路之下，未匹配边比匹配边多一条，所以就可以多一对匹配点。

联系

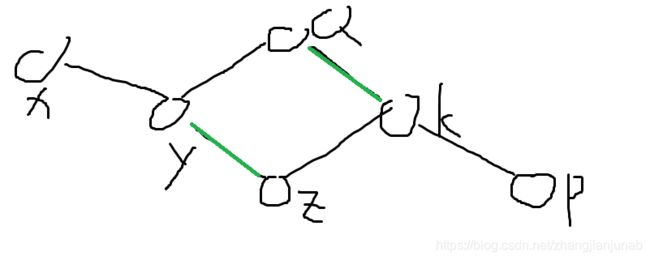
但是如何从k找回x呢？我们目前知道y、z可以用match联系，但z、k和x、y呢？

于是我们设定一个pre数组，$pre[y]=x,pre[k]=z$

其实就相当与是未匹配边的联系，不过是单向反过来的而已。

而且pre不能改，这里不需要理解，我们在后面会慢慢讲。

BFS神力

带花树我们使用BFS进行搜索的。

我们标mark标记，0表示没找过，1表示出去找的点，2代表在家呆着的点，起点为1号点，当我们找到一个点时，如果他没匹配过，代表找到增广路，结束，匹配过，标记他为2，标记他的配偶为1，让他的配偶继续找未匹配边。

奇环

我们找到了A,x,y,Q,z,P,Q,k，但是k找到了Q，而Q是什么呢？

Q是1类点！

这个时候，我们会发现：y,z,k,Q,p只要有一个点找到的匹配点，然后A,X匹配，y,z,k,Q,p的另外四个点也各自匹配，就可以多一个点了。

所以当我们找到一个1类点，我们就把奇环（y,z,k,P,Q）当成一个点，简称开花，我们把这朵花里面的点全部设成1号点，且我们需要把未匹配边的两个点的pre互相设置（之前只是单向设置），当然，一些情况pre不能改，代码见。

细节见代码。

偶环

我们现在用BFS找到了x,y,z,k,Q（找不到P，因为k->p是未匹配边）

但是，Q又找到了y，发现了一件事情，y被找过了，而且还是2类点，这就说明这是个偶环，但是这不是奇环，如果我们重复奇环的过程，我们会发现偶环里面只剩奇数个点，必然会破坏原本的匹配，所以偶环我们什么也不理，没有特殊情况。

LCA

其实指的就是BFS路径上的最近公共祖先，不过需要注意的是，奇环是一个点

int  vis[N]/*标记*/,ts/*时间戳*/;
int  LCA(int  x,int  y)
{
    ts++;//时间增加
    while(x!=0)
    {
        x=find(x);
        vis[x]=ts;
        x=pre[match[x]];
    }
    while(y!=0)
    {
        y=find(y);/*奇环*/if(vis[y]==ts)return  y;
        vis[y]=ts;
        y=pre[match[y]];
    }
    return  0;
}

那么至此，带花树基本讲解结束。

代码

#include
#include
#define  N  11000
#define  M  210000
using  namespace  std;
int  n,m;
struct  node
{
	int  y,next;
}a[M];int  len,last[N];
inline  void  ins(int  x,int  y){len++;a[len].y=y;a[len].next=last[x];last[x]=len;}
int  fa[N];
int  find(int  x){fa[x]!=x?fa[x]=find(fa[x]):0;return  fa[x];}//判断是否在一朵花里面
inline  void  unit(int  x,int  y){int  tx=find(x),ty=find(y);tx!=ty?fa[tx]=ty:0;}//合并两个人的fa
int  mark[N]/*mark标记*/,pre[N]/*前一个点*/,match[N]/*匹配点*/;
int  head,tail,list[N];
void  group(int  x,int  r)
{
	int  y,z;
	while(x!=r)
	{
		y=match[x];z=pre[y];
		if(find(z)!=r)pre[z]=y;//如果z原本就在r所在的花里面，z就不能更新，
		if(mark[y]==2)//花里面全是1
		{
			mark[list[tail++]=y]=1;
			if(tail==n+1)tail=1;
		}
		if(mark[z]==2)
		{
			mark[list[tail++]=z]=1;
			if(tail==n+1)tail=1;
		}
		unit(x,y);unit(y,z);//合并
		x=z;
	}
}
int  vis[N],ts;
int  LCA(int  x,int  y)//求LCA
{
	ts++;
	while(x!=0)
	{
		x=find(x);//奇环是个点
		vis[x]=ts;
		x=pre[match[x]];
	}
	while(y!=0)
	{
		y=find(y);//奇环是个点
		if(vis[y]==ts)return  y;
		vis[y]=ts;
		y=pre[match[y]];
	}
	return  0;
}
bool  bfs(int  st)
{
	for(int  i=1;i<=n;i++)fa[i]=i,mark[i]=pre[i]=0;//初始化
	mark[st]=1;list[head=1]=st;tail=2;
	while(head!=tail)
	{
		int  x=list[head++];if(head==n+1)head=1;
		for(int  k=last[x];k;k=a[k].next)
		{
			int  y=a[k].y;
			if(mark[y]==2)continue;//偶环，不管
			if(find(x)==find(y))continue;//一朵花？不管
			if(mark[y]==1)//缩点
			{
				int  r=LCA(x,y);
				if(find(x)!=r)pre[x]=y;//如group里面一样
				if(find(y)!=r)pre[y]=x;
				group(x,r);group(y,r);
			}
			else
			{
				if(!match[y])//找到增广路了！
				{
					int  p1=x,p2=y;
					while(p1!=0)
					{
						int  tt=match[p1];
						match[p1]=p2;match[p2]=p1;
						p2=tt;p1=pre[tt];
					}
					return  true;
				}
				else//没有
				{
					mark[list[tail++]=match[y]]=1;mark[y]=2;
					if(tail==n+1)tail=1;
					pre[y]=x;
				}
			}
		}
	}
	return  false;
}
int  main()
{
	scanf("%d%d",&n,&m);
	for(int  i=1;i<=m;i++)
	{
		int  x,y;scanf("%d%d",&x,&y);
		ins(x,y);ins(y,x);
	}
	int  ans=0;
	for(int  i=1;i<=n;i++)
	{
		if(!match[i])
		{
			if(bfs(i))ans++;
		}
	}
	printf("%d\n",ans);
	return  0;
}

完结撒花