生成式模型（一）：蒙提霍尔问题与贝叶斯定理

一、 生成式模型

这个系列将讨论人工智能领域非常重要、也十分被看好的一类模型：生成式模型（generative model）。因为这类模型不但能根据特征预测结果，还能“理解”数据是如何产生的，并以此为基础“创造”数据，这才是“真正意义上”的人工智能。而且正如费曼¹所说的“What I cannot create, I do not understand（我不能创造的东西，我就不了解）”，生成式模型在某种意义上是真正理解了数据。

生成式模型的理论基础是贝叶斯定理²。这是一个简单而又深刻的数学定理：一方面，它只涉及乘法、除法以及条件概率，推导过程只需要用到高中数学；另一方面，它引出了很多极具哲学思辨色彩的学术概念，比如先验概率、后验概率等，甚至在统计学里也派生出相应的贝叶斯学派。（这篇文章将大量使用条件概率这个数学概率，对此不是特别熟悉的同学，可以参考这篇文章《生成式模型（零）：条件概率》）

贝叶斯定理是深入理解生成式模型的关键，因此这篇文章将深入讨论这个数学定理，以及如何基于它搭建模型。

二、 蒙提霍尔问题

在讨论严谨的数学公式之前，先看一个有趣又引人深思的游戏—蒙提霍尔问题（Monty Hall problem）。参加这个游戏的选手面对3扇关闭的门，其中一扇门的背后是汽车，另外两扇的背后是山羊，但从选手的角度来看，这3扇门是完全一样的。选手需要按如下的步骤选中一扇门，如果选中的门背后是汽车，则他会免费得到汽车，否则什么都得不到。

• 选手做出最初的决定，选择其中一扇门，如图1中标记1所示。
• 主持人会从剩下的两扇门中，打开一扇后面是山羊的门，如图1中标记2所示。
• 这时选手需要再做一次决定，坚持最初的选择或者更改选择。

如果是读者参加这个游戏会怎么选择呢？从直觉上来讲，似乎对于剩下的两扇门，它们背后是汽车的概率是相等的，都为0.5，那么没必要修改自己的最初决定。

但遗憾的是，直觉是错误的：更改选择后的获奖概率远高于坚持最初决定的。事实上，借助Python针对蒙提霍尔问题做一个简单的统计模拟³，可以得到如图1⁴中标记4所示的结果（模拟的代码可在Github上下载）。根据模拟结果，更改后的获奖概率接近70%，而坚持最初选择的获奖概率只有30%左右。

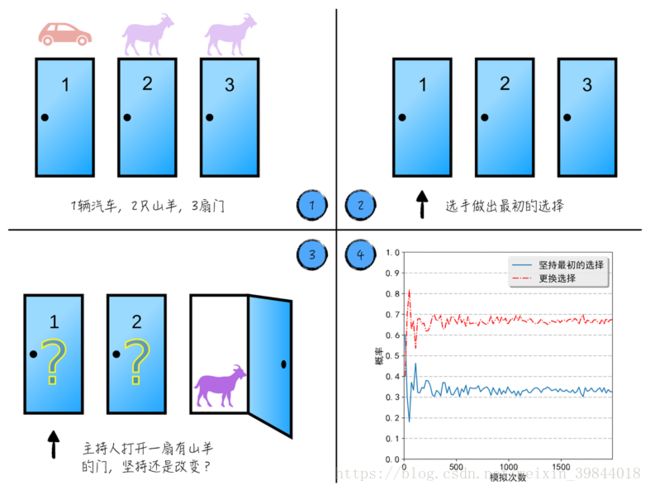图1

为什么会出现如此奇怪的结果呢？直觉上哪里出了错呢？下面将从数学角度给出这个疑问的解释。

三、 条件概率

为了表述清楚，不妨假设选手最初选择的是1号门，而剩下的2号门和3号门对主持人是没有任何差别的。用随机事件$A$表示汽车所在的位置，比如$A=1$表示汽车在1号门的背后。那么在选手做最初选择的时候，汽车在每扇门背后的概率都是一样的，为$1/3$。

$$P(A=1)=P(A=2)=P(A=3)=1/3\text{\hspace{1em}(1)}$$

用随机事件$B$表示主持人打开的门号，比如$B=3$表示主持人打开了3号门。由于2号门和3号门没有差别，那么只需讨论在已知主持人打开3号门的情况下，汽车在1号门以及汽车在2号门的概率。用条件概率来翻译上面这句话就是需要计算$P(A=1|B=3)$以及$P(A=2|B=3)$，其中$P(A=1|B=3)$表示坚持最初选择的获奖概率，而$P(A=2|B=3)$表示更改选择后的获奖概率。根据条件概率的公式，有：

$$P(A=2|B=3)=\frac{P(A=2,B=3)}{P(B=3)}\text{\hspace{1em}(2)}$$

其中$P(A=2,B=3)$表示汽车在2号门且主持人打开3号门的概率。同样根据条件概率的公式，可以得到$P(A=2,B=3)=P(B=3|A=2)P(A=2)$。注意到如果已知汽车在2号门，那么主持人必然会打开3号门，因为规则限制主持人一定要打开后面是山羊的一扇门。由此可得$P(B=3|A=2)=1$，结合公式（1），可以得到公式（3）：

$$P(A=2,B=3)=1\times \frac{1}{3}=\frac{1}{3}\text{\hspace{1em}(3)}$$

接下来需要计算的是$P(B=3)$，即主持人打开3号门的概率。根据概率的定义，可以将这个概率分解为3个概率之和，如公式（4）所示：

$$P(B=3)=P(B=3,A=1)+P(B=3,A=2)+P(B=3,A=3)\text{\hspace{1em}(4)}$$

值得注意的是$P(B=3,A=3)=0$，因为主持人不会打开背后是汽车的门。与公式（3）类似，可以得到$P(B=3,A=1)=P(B=3|A=1)P(A=1)$。由于汽车在1号门时，主持人打开剩下两扇门的概率是一样的⁵，也就是说$P(B=3|A=1)=0.5$，那么$P(B=3,A=1)=1/6$，结合公式（3）可以得到：

$$P(B=3)=\frac{1}{3}+\frac{1}{6}=\frac{1}{2}\text{\hspace{1em}(5)}$$

将公式（5）和公式（3）的结果代入公式（2），得到$P(A=2|B=3)=2/3$。也就是说更换选择后，获奖的概率为，高于坚持最初选择的获奖概率。这与图1中标记4所示的模拟结果是吻合的。

将上面的数学推导用通俗的语言来解释，就是主持人打开3号门这个事件其实隐含了两条信息：

• 汽车在1号门后，主持人是随机打开3号门的；
• 汽车在2号门后，主持人并没有其他选择，只能打开3号门。

这两条信息对选手的最终选择有决定性的影响，而且是完全相反的影响。如果按照第1条信息，应该坚持最初的决定；如果按照第2条信息，则应该更换选择。

不仔细考虑的话，直觉上会认为这两条信息出现的频率是相等的，或者说这两条信息带来的价值是一样的。这会导致我们得到错误的结论：坚持最初决定和更改选择的获奖概率是一样的。为了克服直觉上的缺陷，需要使用合适的数学工具来量化信息带来的价值。而上面的数学推导表明，条件概率可以很好地完成这个任务，这正是贝叶斯框架的精妙之处。

四、 先验概率与后验概率

现在从上面的具体例子回到抽象的数学。对于监督式学习，数据的变量分为自变量和标签变量（因变量）。自变量往往表示事物的表象，是很容易被观测到的，用$X$表示。而标签表示事物的内在，不容易被观测到，也是模型需要预测的量，用$y$表示，则贝叶斯定理的数学公式为：

$$P(y|X)=\frac{P(X|y)P(y)}{P(X)}\text{\hspace{1em}(6)}$$

公式（6）中的$P(X|y)$在学术上被称为先验概率（prior probability），而$P(y|X)$被称为后验概率（posterior probability）。通常可以这样理解，先验概率是用概率的形式表示生活中的常识。比如在蒙提霍尔问题中，在已知汽车在2号门背后的情况下，主持人打开各扇门的概率。而后验概率是通过事物的表象对产生原因的一种猜测，比如同样在蒙提霍尔问题中，在观察到主持人打开3号门的情况下，汽车在2号门背后的概率。用一句话来概括，先验概率是知因求果，后验概率是知果求因。

五、广告时间

这篇文章的大部分内容参考自我的新书《精通数据科学：从线性回归到深度学习》。

李国杰院士和韩家炜教授在读过此书后，亲自为其作序，欢迎大家购买。

另外，与之相关的免费视频课程请关注这个链接

---

1. 理查德·菲利普斯·费曼（Richard Phillips Feynman），美国理论物理学家，量子电动力学创始人，曾被评选为有史以来最伟大的十位物理学家之一。 ↩︎

2. 贝叶斯定理以英国数学家托马斯·贝叶斯（Thomas Bayes）的名字命名 ↩︎

3. 这种统计模拟的方法在学术上被称为蒙特卡洛方法（Monte Carlo method）。该方法使用随机数（或者严谨地说是伪随机数）来解决很多复杂的概率计算问题 ↩︎

4. 图片参考自维基百科 ↩︎

5. 这是因为前面假设了2号门和3号门对主持人没有任何差别。如果假设主持人对某扇门有特殊的偏好，比如在条件允许的范围内总是优先打开3号门，则条件概率不再适合，需要直接使用联合分布概率来解决这个问题（这也是蒙提霍尔问题最难理解的地方）。这种情况下，更换选择后的获奖概率为$P(A=2,B=3)+P(A=3,B=2)=2/3$，具体的计算过程同公式（3）类似。
   更直接地，对于主持人不同的开门策略，使用蒙特卡洛方法模拟，得到的结果是大体一致的 ↩︎