python矩阵中matrix()和array()函数区别

本篇主要介绍内容是矩阵中matrix()和array()函数的区别。主要从以下几方面说起：

1. 使用numpy库生成指定矩阵的方法差异
2. 矩阵性质的差异
3. 在矩阵乘法的不同体现
4. matrix()和array()关于秩的区别
   
5. array()函数和mat()函数之间的转换
   
6. 一些基本知识

1 具体矩阵生成方式的不同：

我们指定以下生成以下矩阵：

我选取此矩阵的原因是：二阶方便计算；矩阵可逆；逆函数好求出（可口算出）。

import numpy as np

a1 = np.array([[1, 2], [3, 4]])
b1 = np.mat([[1, 2], [3, 4]])

a2 = np.array(([1, 2], [3, 4]))
b2 = np.mat(([1, 2], [3, 4]))

a3 = np.array(((1,2), (3,4)))
b3 = np.mat(((1,2), (3,4)))

b4 = np.mat('1 2; 3 4')

print("\n",a1,"\n",b1,"\n",a2,"\n",b2,"\n",a3,"\n",b3,"\n",b4)

输出结果均为：

 [[1 2]
 [3 4]] 

上述函数变化的无非就是把函数大括号内的"[]"换成"()"，但括起来的认为一个整体，不同之处在于  b4 内用引号、空格和分号来产生矩阵，这个方法只可以在  matrix() 函数中使用，不可以写成的 a4 = np.array('1 2; 3 4') 。

2. 矩阵性质的差异

matrix()和 array ()函数都可以通过对象后面加上 .T 得到其转置。但是matrix()还可以在后面加 .H 得到共轭矩阵, 加 .I 得到逆矩阵， array()就不可以，例子如下：

1）转置：

import numpy as np

a1 = np.array([[1, 2], [3, 4]])
b1 = np.mat([[1, 2], [3, 4]])

print(a1.T)
print(b1.T)

输出结果均为：

[[1 3]
 [2 4]]

2）共轭和逆矩阵

import numpy as np
a1 = np.array([[1, 2], [3, 4]])
print(a1.H)

结果为：

AttributeError: 'numpy.ndarray' object has no attribute 'H'

程序最后一行换成：

print(a1.I)

结果为：

AttributeError: 'numpy.ndarray' object has no attribute 'I'

所以，  array() 就不具有 .H   .I ，但是，如果用  b1 计算共轭矩阵和逆矩阵则是可以的，如下：

import numpy as np
b1 = np.mat([[1, 2], [3, 4]])

print(b1.H)
print(b1.I)

共轭矩阵和逆矩阵分别为：

[[1 3]
 [2 4]]
[[-2.   1. ]
 [ 1.5 -0.5]]

3. 在矩阵乘法的不同体现

3.1 观察以下两个输出语句结果的不同：

import numpy as np

a1 = np.array([[1, 2], [3, 4]])
c1 = np.array([[5,6],[7,8]])

b1 = np.mat([[1, 2], [3, 4]])
d1 = np.mat([[5,6],[7,8]])

print("a1乘c1的结果：",a1*c1)
print("b1乘d1的结果：",b1*d1)

输出结果会有不同，分别为：

a1乘c1的结果： [[ 5 12]
 [21 32]]
b1乘d1的结果： [[19 22]
 [43 50]]

于是我们可以得知： array()函数的乘法是矩阵元素所对应位置的两个数进行相乘！而 mat()函数是遵循矩阵乘法规则，所以一定要谨慎使用这两个函数。

不过，无论用array()函数还是mat()函数，若让他们都遵循矩阵乘法的规则，可以对此二阶矩阵应用dot()函数，看下面计算：

print(dot(a1,c1))
print(dot(b1,d1))

输出结果均为：

[[19 22]
 [43 50]]
[[19 22]
 [43 50]]

3.2 根据上文分析，如果我们要算一个矩阵的平方（即两个相同矩阵相乘）。把输出函数变一下，观察一下结果的不同：

print("a1的平方",a1**2)
print("b1的平方",b1**2)

输出结果为：

a1的平方 [[ 1  4]
 [ 9 16]]
b1的平方 [[ 7 10]
 [15 22]]

结果正好验证了3.1的结论。用array()函数求的平方是对应位置之积形成的矩阵。用mat()函数求的平方实际上是遵循矩阵计算得出来的（注意：此时的a1、b1矩阵均是2X2的，遵循矩阵乘法计算，如果换成2X3的矩阵就不可以了，这点应注意）。

总结一下：array()函数的相乘中：*代表点乘（对应元素相乘），dot()代表矩阵乘积。

mat()函数的乘法中：*代表矩阵乘，multiply()代表点乘。

上述观点只是应用于一般场合，具体区别详见：我的其他博客内容

4. matrix()和array()关于秩的区别

关于秩rank的概念，在线性代数(math)中rank表示秩，但是必须明确的是在numpy里rank不是表示秩的概念，是表示维数的概念，姑且这里暂理解为秩。

ndarray.ndim

数组的轴（维度）的个数。在Python世界中，维度的数量被称为rank。

ndarray.shape

数组的维度。这是一个整数的元组，表示每个维度中数组的大小。对于具有n行和m列的矩阵，shape将是(n,m)。

因此，shape元组的长度就是rank或维度的个数ndim。

4.1 对于一维的矩阵：

array()秩是1

mat()秩是2（无论几维，返回的均是2）

>>> from numpy import *
>>> a = array([1,2,3])
>>> a
array([1, 2, 3])
>>> a.shape
(3,)
>>> a.ndim
1
>>> b = mat([1,2,3])
>>> b
matrix([[1, 2, 3]])
>>> b.shape
(1, 3)
>>> b.ndim
2

观察上面得知，a.shape得到的是（3,）,其长度为1，所以a.ndim为1。b .shape得到的是（1,3）,其长度为2，所以a.ndim为2。

4.2 对于二维以上的矩阵：

array()秩是其维数（大于等于2）

mat()的维数返回值必须是2

>>> from numpy import *
>>> a1 = array([[3,4,5],[4,5,6]])
>>> a1
array([[3, 4, 5],
       [4, 5, 6]])
>>> a1.shape
(2, 3)
>>> a1.ndim
2
>>> a2 = mat([[3,4,5],[4,5,6]])
>>> a2
matrix([[3, 4, 5],
        [4, 5, 6]])
>>> a2.shape
(2, 3)
>>> a2.ndim
2

观察上面得知，a1.shape和a2 .shape得到的是（2,3）,其长度为2，所以a1.ndim和a2.ndim都是2。

>>> from numpy import *
>>> b1 = array([[[3,4],[5,6]],[[7,8],[9,10]]])
>>> b1
array([[[ 3,  4],
        [ 5,  6]],

       [[ 7,  8],
        [ 9, 10]]])
>>> b1.shape
(2, 2, 2)
>>> b1.ndim
3
>>> b2 = mat([[[3,4],[5,6]],[[7,8],[9,10]]])
    raise ValueError("matrix must be 2-dimensional")
ValueError: matrix must be 2-dimensional

观察上面得知，b1.shape 得到的是（2,2,2）,其长度为3，所以b1.ndim是3,如果让array()变为mat()时，直接报错，要求矩阵必须是二维的！

5. array()函数和mat()函数之间的转换

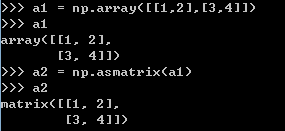
从array()函数到mat()函数用np.asmatrix()

使用交互式命令观察一下：

从 mat()函数到 array()函数用 np.asarray()

使用交互式命令观察一下：

建议在使用中，尽量只使用一种类型的计算，这样避免了计算时候会迷糊。

6. 一些基本知识

• 由于数组array是NumPy中的默认值，大部分返回的是array类型。但给出一个矩阵作为参数，一些函数也可能返回一个数组。 这不应该发生在NumPy函数（如果它是一个错误），但是基于NumPy的第三方代码可能不符合像NumPy这样的类型保存。
• 大多数Numpy函数返回array，然而Scipy里又有一堆返回matrix的函数，搞得很混乱。看到其他网友的方法是：每行矩阵运算代码，都在旁边注释其结果到底是array还是 matrix，什么形状；对于传来的参数，不管是matrix还是array，一律先 A = matrix(A) 显示转换为matrix再说，这就减少了不必要的麻烦。我是觉得大家自己使用可以只用一种类型的，使用多了，记住哪些特殊的函数输出结果类型变了就很容易多了。
• 在numpy中的特殊类型，是作为array的子类出现，所以继承了array的所有特性并且有自己的特殊的地方，专门用来处理线性代数操作。

更多资料参考：http://scipy.github.io/old-wiki/pages/NumPy_for_Matlab_Users