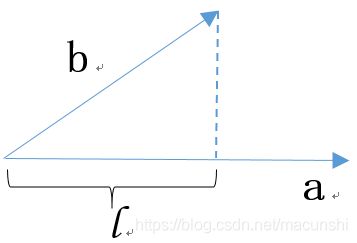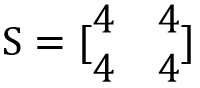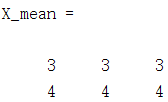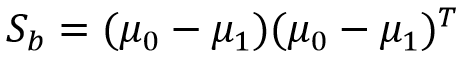线性判别分析（LDA）的一点见解

LDA的中文名字是线性判别分析，以前在机器学习课上老师留过作业，对西瓜书上的数据进行了一次LDA分类，详见博客：

https://blog.csdn.net/macunshi/article/details/80756016，里面有详细的MATLAB代码，后来在实际的课题项目里也用到了LDA，发现对某些数据二分类的效果还是很不错的，现在复习这个知识，顺便写一下我对LDA的一些见解。

（1）关于简单投影问题

           

b向量投影到a向量的长度怎么计算呢？就是右上边这个式子，如果a的模为1,那么 l 的长度就变成了第三行的式子，a向量的作用就是给定了一个方向。

（2）关于协方差矩阵

我们先不考虑它的意义，看一下协方差矩阵是怎么算的。

比如我这儿有了一组数：

        

把它看成三个二维的点，记为x1、x2、x3， 也就是三组观察量，记为n组，每组有两个特征。我们先求出X所有变量的均值x_mean,然后根据下面的公式求得X的协方差矩阵S。

这个求协方差矩阵的式子是不是和数理统计里面方差的定义异曲同工！

当然你也可以把x_mean扩展成X_mean如下：

然后协方差矩阵就可以写成这样了：

其实两者的计算是一样的，数据是有n维特征的那么协方差矩阵就是n*n的。

（3）LDA是怎么推导的呢？

西瓜书讲的不错，我们先借西瓜书上的一张图：

我们假设有图上两类点，用Xi,ui,Si分别表示不同类的点集合、均值、协方差矩阵。将这些点投影到直线w上，那么就有：

以上求出来全是实数。

我们对投影以后的期望是什么呢？就是像图中一样，同类尽可能的紧凑，不同类尽可能的分开。所以我们要使两个投影后点集的方差和尽可能的小，而两个投影中心点的距离尽可能的大，也就可以得到如下目标函数：

这样我们就引出了类内散度矩阵Sw，w是within的首字母，即内部的意思。

同时还有类间散度矩阵Sb, b是between的首字母，即之间的意思。

所以现在明白白这两个重要的矩阵是怎么来的了吧。

于是目标函数就可以写成下面的形式了：

然后这就是一个最优化的问题了。

（4）关于瑞利商

这个东西就是矩阵理论里有点难的东西了，以前上矩阵理论课的时候就学的迷迷糊糊的，老师纯讲理论根本听不懂啊，我倒是知道学过瑞利商这个玩意，但是干嘛的有什么意义一头懵逼。

现在又把它翻出来一看，原来在这等着呢。当年老师要是从机器学习讲起，再讲矩阵理论的应用，我应该学会的知识还多一点。

关于瑞利商，看这个大哥的帖子：https://www.cnblogs.com/pinard/p/6244265.html，这位大哥应该对机器学习有深入的理解，我截一部分过来看看。

 回头看，我们的目标函数就是广义瑞利商。

如果你是不理解矩阵的推导，那就先记住一条瑞利商的定理：

瑞利商的取最大值的时候，x向量为 A逆矩阵 的最大特征值 所对应的特征向量。

其中A矩阵是Hemitan矩阵，这个特征向量的模为1，此时你在想想博文开头讲了什么。

通过上面图中推导的内容，你大概也就猜出对于目标函数广义瑞利商最大值的一个定理了：

广义瑞利商的取最大值的时候，w向量为 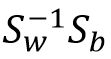矩阵 的最大特征值 所对应的特征向量。w表示一个投影的方向。

所以你现在知道LDA怎么求最佳投影向量w了。