动态规划--数塔

数塔是动态规划的一道经典题
认识数塔前，先认识一下动态规划，动态规划不是一种特定的算法，而是一种具有较强的技巧性的手段，或者说是思想，但所有动态规划的题离不开两个核心：
1.状态
2.状态转移方程
当我们抓住这两个核心，我们的问题就能解决一大半！
—————————————————————————————————————
题目：

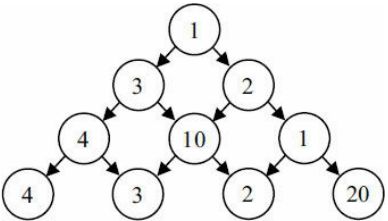
图片上便是一个数塔，现在要解决的问题是，从数塔顶层到底层，沿途将权重（即数值）相加和最大是多少？

分析：
首先再回想一遍动态规划的两个核心。
状态分析：我们会发现，当在每个节点都会做一个选择，（例如：在1时，是选择左还是选择右）
而选择了左或者右的时候又继续会有选择，我们此时马上就会想到递归（见a）
状态转移方程分析：题目要求最大的走法，所以我们可以初步得出一个方程雏形
a[选择后的结果]=b[节点]+max(a[左],a[右])
现在就需要一点点技巧性了，如何将方程雏形改成真正的状态转移方程
此处我们给出一个二维数组的处理办法，如图所示：

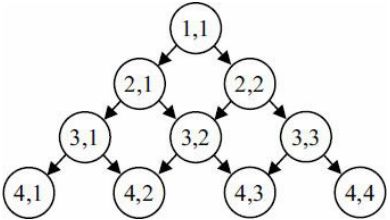
即可得出状态转移方程：
a[i,j]=b[i,j]+max(a[i+1,j],a[i+1,j+1])
理解了题目的状态，得出状态转移方程后，便要考虑计算的问题了
- a
-递归计算
！！注意边界处理，递归没有什么要讲的，直入代码

int dp(int i,int j)
{
	if(i<=n)
		return b[i,j]+max(dp(i+1,j),dp(i+1,j+1))
	if(i>n)
		return 0;
}

例子代码：

#include
#include
using namespace std;
int a[105][105],m;
int dp(int i,int j)
{
    if(i<=m)
        return a[i][j]+(max(dp(i+1,j),dp(i+1,j+1)));
    if(i>m)
        return 0;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&m);
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=i;j++)
            {
                scanf("%d",&a[i][j]);
            }
        }
        printf("%d",dp(1,1));
    }
    return 0;
}

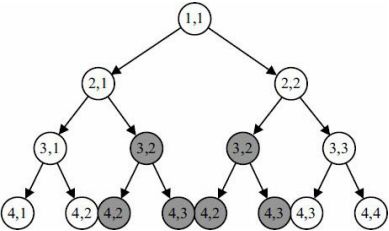
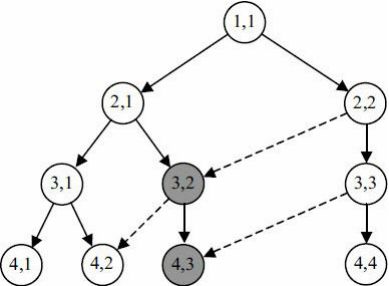
递归算法保证子结构为最优解，所以上一结构也是最优，所以可以得出最大数值路径，但是会产生大量的重复计算，如图片2中会将（3，2）（4，2）（4，3）重复计算两次，如果数塔层数过大，那么效率是很低的，所以孕育而生了递推计算（见b） 记忆化搜索（见c）

- b
递推计算
！！边界处理，递推采用的是一种逆向思维，从数塔最后一层进行处理，比递归计算处理更加的简洁，
在大多数情况下（每个决策时间一样），递推法的时间复杂度是：状态总数×每个状态的决策个数×决策时间。

	for(int i=1;i=1;i--)
	{
		for(int j=1;j<=i;j++)
		{
			b[i][j]=a[i][j]+max(b[i+1][j],b[i+1][j+1]);
		}
	}

例子代码：

#include
#include
using namespace std;
int a[105][105];
int b[105][105];
int m;
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&m);
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=i;j++)
            {
                scanf("%d",&a[i][j]);
            }
        }
    for(int i=1;i<=m;i++)
		b[m][i]=a[m][i];
	for(int i=m-1;i>=1;i--)
	{
		for(int j=1;j<=i;j++)
		{
			b[i][j]=a[i][j]+max(b[i+1][j],b[i+1][j+1]);
		}
	}
	printf("%d",b[1][1]);
   }
   return 0;
}

- c
记忆化搜索
记忆化搜索是递归的优化版本，利用另一个数组将处理过的数组记录，达到优化目的
记录处理：利用memset(b,－1,sizeof(b))将b[ ][ ]数组都初始化为-1，当数组进行过处理直接返回当前数值即可

int dp(int i,int j)
{
		if(b[i][j]>=0)
			return b[i][j];
		if(i<=m)
			b[i][j]=a[i][j]+max(dp(i+1,j),dp(i+1,j+1));
		if(i>m)
			return 0;
} 

例子代码和递归没多大差别，就是要注意每次进行需要将数组b[][]进行初始化为-1为下一次计算做准备
递归与记忆化搜索的区别 见下图：

图示已将优化体现的很明显了~

注：
1.片段代码或者语言如有错误望谅解并请指出。
2.图摘自算法竞赛入门经典第二版，侵权请联系博主删除/笑哭/笑哭。