线性表（顺序存储）

1.特征

数据元素之间仅具有单一的前驱和后继关系。

2.逻辑结构

2.1逻辑结构图

2.2抽象数据类型定义

线性表需要可以完成存取访问，插入删除等基本操作。其抽象数据类型定义为：

ADT List
	DataModel
		线性表中元素具有相同类型，相邻元素具有前驱和后继关系
	Operation
		InitList
			输入：无
			功能：线性表的初始化
			输出：空的线性表
		CreatList
			输入：n个数据元素
   			功能：建立一个线性表
   			输出：具有n个元素的线性表
		DestroyList
   			输入：无
      			功能：销毁数据表      			
      			输出：释放线性表的存储空间
      		PrintList
      			输入：无
      			功能：遍历操作，按序号一次输出线性表中的元素
      			输出：线性表的各个数据元素
      		Length
      			输入：无
      			功能：求线性表的长度
      			输出：线性表中数据元素的个数
      		Locate
      			输入：数据元素x
      			功能：按值查找，在线性表中查找值等于x的元素
      			输出：如果查找成功，返回元素x在线性表中的序号，否则返回0
      		Get
      			输入：元素的符号i
      			功能：按位查找，在线性表中查找序号为i的数据元素
      			输出：如果查找成功，返回序号为i的元素值，否则返回查找失败信息
      		Insert
      			输入：插入位置i和待查元素x
      			功能：插入操作，在线性表的第i个位置插入一个新元素x
      			输出：如果插入成功，返回
		Delete
			输入：删除位置i
			功能：删除操作，删除线性表中的第i个元素
			输出：如果删除成功，返回被删元素，否则返回删除失败信息
		Empty
			输入：无
			功能：判空操作，判断线性表是否为空表
			输出：如果是空表，返回1，否则返回0
endADT		

操作由三部分组成：1.输入 2.功能 3.输出

2.3顺序存储结构及实现

2.3.1存储结构定义

使用一维数组实现顺序表，可以通过数组的下标得到顺序表元素的位置。而使用数组，我们就需要给数组在内存中分配固定长度的空间。用MaxSize表示数组的长度，用length表示线性表的长度。同时，顺序表是在我们定义的数组的范围中之中的，所以数组的长度一定大于顺序表的长度，即MaxSize一定大于length。
如同现在有一栋楼，我们现在把其中的一层买了下来，这样这层楼的“屋子”只有我们能用了（定义数组）。假设这层楼有十个“屋子”分别是1-10号，这是我们的MaxSize就是“屋子的个数”，即为10。
现在，我们可以使用这十个“屋子”了，我们可以把我们使用的“屋子”叫做“家”（顺序表的元素），把家的个数叫做length，无论我怎么使用，“家”的号码绝不可能超出“屋子”号码的范围，即MaxSize一定大于length。

数组的长度和线性表的长度具有不同含义：

下面给出顺序表的存储结构定义：

#define Maxsize 100	//假设顺序表最多存放100个元素
typedef int DataType;	//定义线性表的数据类型，假设为int型
typedef struct
{
 DataType data[Maxsize];	//存放数据元素的数组
 int length;	//线性表的长度
} SeqList;

2.3.2实现

上文已经提到“操作由三部分组成：1.输入 2.功能 3.输出”，
当我们制作操作接口时，我们也需要考虑三部分：
1.输入是否合法
2.功能如何实现
3.根据输入的合法性和功能的结果，确定输出

（1）初始化顺序表

所谓初始化，就是把一个东西恢复到最初的状态，对于线性表来说，就是把所有的元素都删除，只留下一个有表结构的空表。我们把顺序表的长度length初始化为0，顺序表里面的原有元素就无法使用了（事实上在数组里还存在），这样，就能造成，顺序表中的所有元素都被删除的效果，也就是完成了初始化。

即，初始化顺序表只需将顺序表的长度length初始化为0，C语言实现如下

void InitList(SeqList *L)
{
 L->length=0;
}

（2）建立顺序表

建立顺序表，我们只需要把数组中的元素赋给顺序表即可（不要忘了设置顺序表长度）。
即，建立顺序表需要四步：
1.判断输入合法性，不合法则返回0；
2.把数组中的元素赋给顺序表；
3.设置顺序表长度；
4.建立成功，返回1；

建立顺序表的操作顺序图：

int CreatList(SeqList *L,DataType a[],int n)
{
 if(n>Maxsize)		//1.判断输入合法性，不合法则返回0
 {
  printf("顺序表空间不够，无法建立顺序表\n");
  return 0;
 }
 for(int i = 0;i<n;i++)		//2.把数组中的元素赋给顺序表
  L->data[i]=a[i];
 L->length=n;		//3.设置顺序表长度
 return 1;	//4.建立成功，返回1
}

（3）销毁顺序表

顺序表是静态存储分配，在顺序表变量退出作用域时自动释放该变量所占内存单元，因此，顺序表无须销毁。

（4）判空操作

顺序表的判空操作只需判断长度length是否为0，如果为0，就说明顺序表为空，C语言实现如下：

int Empty(SeqList *L)
{
 if(L->length==0)
  return 1;	//顺序表为空返回1
 else return 0;
}

（5）求顺序表的长度

在顺序表的存储结构定义中用结构体成员length保存了像线性表的长度，因此，求线性表的长度只需返回成员length的值，C语言实现如下：

int Length(SeqList *L)
{
 return L->length;
}

（6）遍历操作

在顺序表中，遍历操作既是按下标依次输出各元素，C语言实现如下：

void PrintList(SeqList *L)
{
 for(int i=0;i<L->length;i++)
  printf("%d ",L->data[i]);	//输出线性表的元素值，假设为int型
}

（7）按值查找

在顺序表中实现按值查找操作，需要对顺序表中的元素依次进行比较，如果查找成功，返回元素的序号（不是下标，元素的序号与数组的下标差1），否则返回查找失败的标志0。

int Locate(SeqList *L,DataType x)
{
 for(int i=0;i<L->length;i++)
  if(L->data[i]==x)
   return i+1;		//返回序号
 return 0;	//退出循环，说明查找失败
}

（8）按位查找

顺序表中第i个元素存储在数组中下标为i-1的位置。函数Get的返回值表示返回是否成功（0代表不成功，1代表成功）。若查找成功，通过指针参数返回查找到的元素值，C语言实现如下：

int Get(SeqList *L,int i,DataType *ptr)
{
 if(i<i||i>L->length)
 {
  printf("查找位置非法，查找失败\n");
  return 0;
 }
 else
 {
  *ptr=L->data[i-1];
  return 1;
 }
}

（9）插入操作

插入前：

插入后：

在表的第i（1<=i<=n+1）个位置插入一个新元素x，使长度为n的线性表变成长度为n+1的线性表。
必须从最后一个元素开始移动。
方法的实现有五步
1.如果表满了，则输出上溢错误信息，插入失败；
2.如果元素的插入位置不合理，则输出位置错误信息，插入失败；
3.将最后一个元素直至第i个元素分别向后移动一个位置；
4.将元素x填入位置i处；
5.表长加1；

int Insert(SeqList *L,int i,DataType x)
{
 if(L->length>=Maxsize)	//1.如果表满了，则输出上溢错误信息，插入失败；
 {
  printf("上溢错误，插入失败\n");
  return 0;
 }
 if(i<1||i>L->length)	//2.如果元素的插入位置不合理，则输出位置错误信息，插入失败；
 {
  printf("位置错误，插入失败");
  return 0;
 }
 //j表示元素序号
 for(int j=L->length;j>=i;j--)	//3.将最后一个元素直至第i个元素分别向后移动一个位置；
  L->data[j]=L->data[j-1];
 L->data[i-1]=x;	//4.将元素x填入位置i处；
 L->length++;	//5.表长加1；
 return 1;
}

（10）删除操作

删除前：

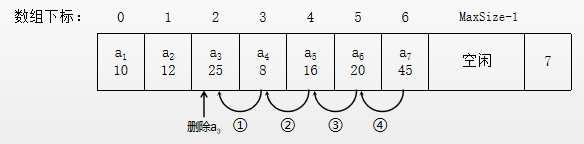
删除后：

将表的第i（1<=i<=n）个元素删除，使长度为n的线性表变成长度为n-1的线性表。
必须从i+1个元素开始移动，并且要取出被删元素（因为在删除时有可能发生误删，如回收站的作用）。
方法的实现有五步
1.如果表空，则输出下溢错误信息，删除失败；
2.如果元素的删除位置不合理，则输出位置错误信息，删除失败；
3.取出位置i的元素；
4.将i+1个元素直至最后一个元素分别向前移动一个位置；
5.表长减1；

int Delete(SeqList *L,int i,DataType *ptr)
{
 if(L->length==0)	//1.如果表空，则输出下溢错误信息，删除失败；
 {
  printf("下溢错误，删除失败\n");
   return 0;
 }
 if(i<1||i>L->length)	//2.如果元素的删除位置不合理，则输出位置错误信息，删除失败；
 {
  printf("位置错误，删除失败\n");
  return 0;
 }
 *ptr = L->data[i-1];	//3.取出位置i的元素；
  //j表示元素序号
 for(int j=i;j<L->length;j++)	//4.将i+1个元素直至最后一个元素分别向前移动一个位置；
  L->data[j-1]=L->data[j];
 L->length--;	//5.表长减1；
 return 1;
}