图像插值
1、最邻近元法
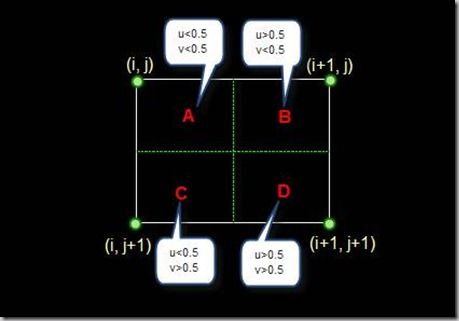
这是最简单的一种插值方法,不需要计算,在待求象素的四邻象素中,将距离待求象素最近的邻象素灰度赋给待求象素。设i+u, j+v(i, j为正整数, u, v为大于零小于1的小数,下同)为待求象素坐标,则待求象素灰度的值 f(i+u, j+v) 如下图所示:
如果(i+u, j+v)落在A区,即u<0.5, v<0.5,则将左上角象素的灰度值赋给待求象素,同理,落在B区则赋予右上角的象素灰度值,落在C区则赋予左下角象素的灰度值,落在D区则赋予右下角象素的灰度值。
最邻近元法计算量较小,但可能会造成插值生成的图像灰度上的不连续,在灰度变化的地方可能出现明显的锯齿状。
1 function outImg=nearest(inImg, outSize) 2 outImg=zeros(outSize(1),outSize(2)); 3 [m,n] = size(inImg); 4 for row=1:outSize(1) 5 for col=1:outSize(2) 6 outImg(row,col) = inImg(ceil(row/outSize(1)*m),... 7 ceil(col/outSize(2)*n)); 8 end 9 end 10 end
2、双线性内插法
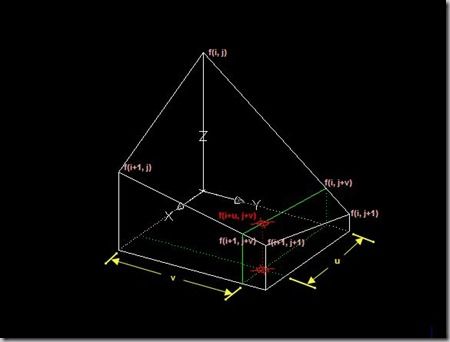
双线性内插法是利用待求象素四个邻象素的灰度在两个方向上作线性内插,如下图所示:
对于 (i, j+v),f(i, j) 到 f(i, j+1) 的灰度变化为线性关系,则有:
f(i, j+v) = [f(i, j+1) - f(i, j)] * v + f(i, j)
同理对于 (i+1, j+v) 则有:
f(i+1, j+v) = [f(i+1, j+1) - f(i+1, j)] * v + f(i+1, j)
从f(i, j+v) 到 f(i+1, j+v) 的灰度变化也为线性关系,由此可推导出待求象素灰度的计算式如下:
f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) + u * v * f(i+1, j+1)
双线性内插法的计算比最邻近点法复杂,计算量较大,但没有灰度不连续的缺点,结果基本令人满意。它具有低通滤波性质,使高频分量受损,图像轮廓可能会有一点模糊。
1 function outImg=bilinear(inImg,outSize) 2 % f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) 3 % + u(1-v)f(i+1,j) + uvf(i+1,j+1) 4 outImg = zeros(outSize); 5 inSize = size(inImg); 6 for outRow = 1:outSize(1) 7 for outCol = 1:outSize(2) 8 inRow = (outRow+0.5)/outSize(1)*(inSize(1)-0.5); 9 inCol = (outCol+0.5)/outSize(2)*(inSize(2)-0.5); 10 11 i = floor(inRow); 12 u = inRow - i; 13 j = floor(inCol); 14 v = inCol - j; 15 if i==0, i=1; end 16 if j==0, j=1; end 17 18 outImg(outRow,outCol) = (1-u)*(1-v)*inImg(i,j) + ... 19 (1-u)*v*inImg(i,j+1) + u*(1-v)*inImg(i+1,j) + ... 20 u*v*inImg(i+1,j+1); 21 end 22 end 23 end
3、三次内插法
该方法利用三次多项式S(x)求逼近理论上最佳插值函数sin(x)/x, 其数学表达式为:
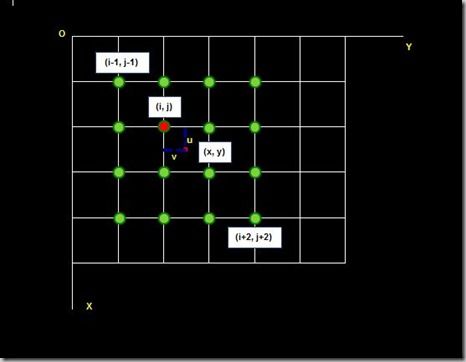
待求像素(x, y)的灰度值由其周围16个灰度值加权内插得到,如下图:
待求像素的灰度计算式如下:
f(x, y) = f(i+u, j+v) = ABC
三次卷积法考虑一个浮点坐标(i+u,j+v)周围的16个邻点,目的像素值f(i+u,j+v)可由如下插值公式得到:
f(i+u,j+v) = [A] * [B] * [C]
[A]=[ S(u + 1) S(u + 0) S(u - 1) S(u - 2) ]
┏ f(i-1, j-1) f(i-1, j+0) f(i-1, j+1) f(i-1, j+2) ┓
[B]=┃ f(i+0, j-1) f(i+0, j+0) f(i+0, j+1) f(i+0, j+2) ┃
┃ f(i+1, j-1) f(i+1, j+0) f(i+1, j+1) f(i+1, j+2) ┃
┗ f(i+2, j-1) f(i+2, j+0) f(i+2, j+1) f(i+2, j+2) ┛
┏ S(v + 1) ┓
[C]=┃ S(v + 0) ┃
┃ S(v - 1) ┃
┗ S(v - 2) ┛
┏ 1-2*Abs(x)^2+Abs(x)^3 , 0<=Abs(x)<1
S(x)={ 4-8*Abs(x)+5*Abs(x)^2-Abs(x)^3 , 1<=Abs(x)<2
┗ 0 , Abs(x)>=2
S(x)是对 Sin(x*Pi)/x 的逼近(Pi是圆周率——π)
插值曲线公式sin(x*PI)/(x*PI),如图: