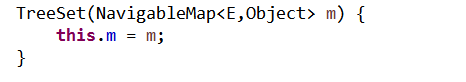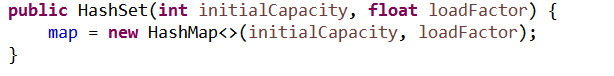JAVA总结(五)----- 容器(二)-----Set
注:以下概念与代码均参考自:《java编程思想》、《算法导论》、《Effective Java》、《数据结构和Java集合框架》
目录
一、为什么选择Set
二、基于红黑树实现 —— TreeSet
1、红黑树
2、TreeSet
三、基于散列表实现 —— HashSet
1、散列表
2、HashSet
四、内部链表的散列表 —— LinkedHashSet
五、equals、hashCode、compareTo方法
1、equals方法
2、hashCode方法
3、compareTo方法
附录A
附录B
一、为什么选择Set
在上一片文章中,已经介绍了Collection接口保存一组元素的序列,这些序列需要遵循一个多个的规则存放。List采用元素存放的顺序存放元素,利用索引检索元素,并且可以用有重复的元素。
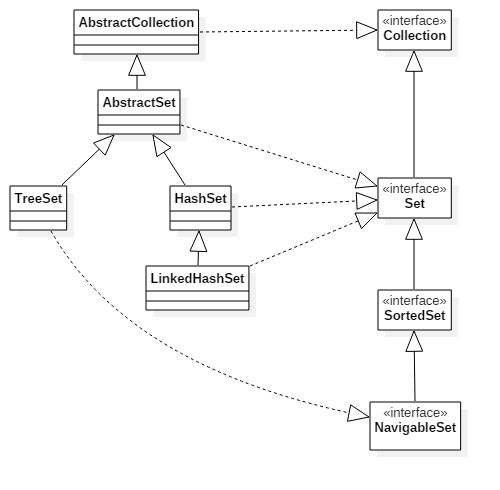
Set接口:Set继承了Collection接口,提供另外一种元素的存放的规则:存放的元素不能有重复,存放的顺序基于Set的不同实现。使用Set最常被用作测试归属性,这使得必须很容易地询问某个元素是否在Set中,因此检索就变成Set最常用的操作。Set的实现与List实现不同,它采取更复杂,更有针对性的数据结构。比如,HashSet采用散列表来实现快速查找。TreeSet采用红黑树维护元素存入的顺序。
| Set(interface) |
存入Set的元素的每个元素必须唯一,因为Set不保存重复元素。存入Set的元素也必须重写equals()以确保元素的唯一性。Set接口不保证维护元素的次序。 |
| HashSet | 为快速检索而设计的Set,采用散列表实现。存入HashSet中的元素必须重写hashCode()生成对象的在散列表中的桶位 |
| TreeSet | 维护次序的Set,采用红黑树为它的实现。使用它可以提取有序的序列,存入的元素必须实现Comparable接口。使用红黑树可以获取更高检索性能的检索树 |
| LinkedHashSet | 具有HashSet的查询速度,且内部使用链表维护元素的顺序(插入的次序)。于是在使用迭代器遍历Set时,结果会按照元素的插入次序显示。存入的元素也必须实现hashCode() |
二、基于红黑树实现 —— TreeSet
注:附录A为我手写的红黑树源码,在实现红黑树的功能下,还支持用泛型指定存储数据的类型。另外我重写了toString方法,使得输出该对象时可以按照中序遍历输出。另外存储数据,和删除数据的方法为add(),与delete()我封装了红黑树的源码。
1、红黑树
注:以下内容参考自《算法导论》
①、为什么TreeSet使用红黑树
对于二叉搜索树,其字典的操作的averageTime(n)为O(lgn),但在最坏的情况下,比如说二叉树退化成链表那么其字典操作需要worstTimeO(n)为O(n)。红黑树的插入删除操作等的字典操作都具有O(lgn)的性能(它不会像搜索树那样退化成链表),而AVL也具有相同的性能。但为什么使用红黑树进行实现TreeSet而不使用AVL。其原因是,AVL树是一颗高度平衡的树,对于插入和删除都必须满足平衡性,所以AVL需要更多的旋转维护平衡性,而红黑树最多只进行三次旋转就可以完成操作。所以红黑树的统计性能方面要由于AVL树。此外,红黑树通常应用于关联数组。
②、什么红黑树
红黑树是一颗近似平衡的二叉搜索树,可以保证在最坏情况下基本的动态集合操作的时间复杂度为O(lgn)。通过对任何一条从根到叶子的路径上各个结点的颜色进行约束,红黑树保证没有一条路径会比其他路径长2倍。
一颗红黑树是满足下面红黑性质的二叉搜索树:
1)每个结点或红色,或是黑色
2)根结点是黑色
3)每个叶子结点是黑色的
4)如果一个结点是红色,那么它的孩子都是黑色
5)对每个结点,从该结点到其所有后代的简单路径上,均包含相同数目的黑色结点。
黑高(black-height)定义:从某个结点(不含该结点)出发到达一个叶子结点的任意路径上的黑色结点个数称为该结点的黑高。同样的从根结点出发到达一个叶子结点的任意路径上的黑色结点个数称为该红黑树的黑高。
引理:一个有n个内部结点的红黑树的高度至多为2lg(n+1)
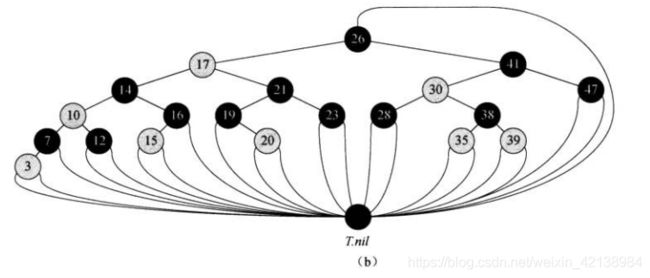
一颗红黑树的每个结点包含五个字段:color、item、left、right和p。如果一个结点没有孩子结点或者双亲结点,那么该结点的相应属性值NIL,我们使用哨兵sentry T.nil替代NIL,也就说是哨兵结点是所以叶子结点与根结点的双亲结点。下图为一颗红黑树。
②、旋转
当某颗树违反了平衡性质,或者红黑性质。需要通过修改指针维护这些性质,那么旋转(Rotation)就是一种能保持二叉搜索树性质的搜索树局部指针修改操作。
旋转操作分为:左旋与右旋。下面介绍这两种操作的实现。
1)左旋:前提:旋转结点x必须要有右孩子y。
a)不变量:x的左孩子,y的右孩子
b)首先把y的左孩子称为x的左孩子。
c)x的双亲成为y的双亲
d)x成为y的左孩子
下面是其伪代码:
leftRorate(x) {
// x没有右孩子时,退出左旋操作
if (x.right == null)
return ;
y = x.right;
// y的左孩子成为x的右孩子
x.right = y.left;
if (y.left != null)
y.left.p = x;
// y指向x的双亲
y.p = x.p;
// 如果x的双亲为null,那么根结点为y
if (x.p == null)
root = y;
// 如果x是其双亲的左孩子,那么y成为x双亲的左孩子
else if (x == x.p.left)
x.p.left = y;
// 否则成为右孩子
else
x.p.right = y;
// x成为y的左孩子
y.left = x;
x.p = y;
}2)右旋:右旋的操作与左旋的操作时对称的。前提:旋转结点x要有左孩子y
a)不变量:x的右孩子,y的左孩子
b)首先把y的右孩子称为x的的左孩子
c)x的双亲称为y的双亲
d)x成为y的右 孩子
下面是其伪代码:
rightRotate(x) {
// x的左孩子不能为null
if (x.left == null)
return ;
y = x.left;
// y的右孩子成为x的左孩子
x.left = y.right;
if (y.right != null)
y.right.p = x;
// 下面同左旋
y.p = x.p;
if (x.p == null)
root = y;
else if (x = x.p.left)
x.p.left = y;
else
x.p.right = y;
// x成为y的右孩子
y.right = x;
x.p = y;
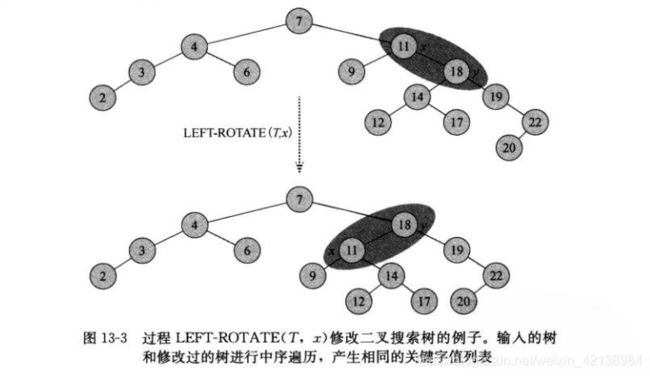
}对于leftRotate与rightRotate都在O(1)时间内完成。在旋转过程中只有指针改变,其它的属性都保持不变。下面看一个具体的左旋图。
③、插入
红黑树的插入操作可以在包含n个结点O(lgn)时间内完成。插入操作初始时,通过将新结点z着为红色插入到红黑树中,然后维护红黑树性质。
1)插入:红黑树的插入与搜索树的插入类似。首先初始化遍历指针x(用于寻找插入的合适位置)和x的双亲指针y(y的存在是因为x找到合适位置时,x为null,此时无法获取它的双亲指针,也就无法就行链接操作)。在while循环中,通过对待插入元素z与x进行值比较,确定z向树的那个方向进行插入。在最后,把插入元素z的孩子指向哨兵,把涂上红色,调用维护红黑性质的方法。下面是其实现的伪代码
redBlackInsert(x) {
// 初始化时,y指向哨兵
y = sentry;
// x从root开始遍历
x = root;
while (x != sentry) {
y = x;
if (z.key < x.key)
x = x.left;
else
x = x.right;
}
// 退出循环后,x找到合适的插入位置,那么z指向x的双亲
z.p = y;
// y是哨兵,说明z是树中第一个元素,那么root指向它
if (y == sentry)
root = z;
// z小于y,那么z成为y的左孩子
else if(z.key < y.key)
y.left = z;
// 否则成为右孩子
else
y.right = z;
// z的孩子指向哨兵,z着为红色
z.left = sentry;
z.right = sentry;
z.color = RED;
// 维护红黑性质
redBlackInsertFixup(z);
}2)维护红黑性质:首先看看那些性质会被破坏
a)性质1,插入后此时树中结点要么是红色,要么是黑色。满足
b)性质2:插入后,如果插入的元素是根结点,那么不满足此条(因为插入z后,将其着为红色)
c)性质3:插入后,因为插入的孩子指向哨兵,哨兵为黑色结点。满足
d)性质4:假设插入后,z的双亲红结点,z也为红色。违反性质4。不满足
e)性质5:因为插入的红色,所以对于包含插入结点的简单路径上黑色结点数目将保持不变。满足
综上,插入的结点将违反性质2、或性质4.。
下面说明while循环中保持的3个循环不定式:
a.结点z是红结点
b.如果z.p是根结点,那么z.p是黑结点
c.如果有任何红黑性质被破坏,则至多有一条被破坏。或是性质2、或是性质4.。其原因是z为根结点时,那么就不可能违反性质4(性质4需要双亲结点)。如果z不是根结点,那么就不可能违反性质2。下面给出证明
*初始化:在循环第一次迭代之前,从一颗正常的红黑树开始,并新值红结点z
a.当循环之前,z是新增的红结点
b.如果z.p是根,那么z.p开始为黑色
c. 如果违反性质2,则红色的结点一定是新增的结点z,它是树中唯一的内部结点。如果违反性质4、由于z的孩子都是黑色,且该树在z加入之前没有其他性质的违反,那么必然是z和z.p为红色。
*循环:进入循环的条件是z.p为黑结点,那么必然不会违反性质2,只能违反性质4,此时z结点只能是根结点。也就是说进入循环只能破坏性质4。所以此时z与z.p都为红色。回到循环,在循环中实际需要考虑六种情况。其取决于z.p是z.p.p的左孩子还是右孩子,与z的叔结点(z.p的兄弟结点)是红色还是黑色和z是z.p的左孩子还是右孩子。下面分条件讨论这些情况。
注:当进入循环后,z.p为红结点,那么z.p.p只能是黑结点(因为不能违反性质4)。
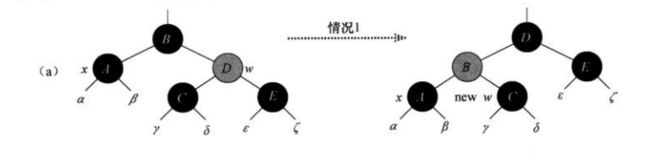
a、情况a:当z.p为z.p.p的左孩子,且叔结点y为红色时
此时z、z.p与y都为红结点,那么把z.p与y着为黑色,解决z与z.p都为红色的问题。并把z.p.p着为红色,解决性质5问题。此时z' = z.p.p进入下次循环。下面证明循环不定式:
1、这次迭代把z' = z.p.p着为红色,所以结点z'在下次迭代前都为红色
2、如果这次迭代中z'.p的颜色不会改变,如果它是根的话,那么在这次迭代之前就已经为黑色。
3、如果z'在下次迭代开始时是根结点,则在这次迭代过程中修正了被唯一破坏的性质4。并且z‘为红色那么性质2成为了唯一破坏的性质
如果z'在下次迭代开始时不是根结点,则不会违反性质2。如果z'.p为黑色,那么也不会违反性质2。如果z'.p为红色,那么也就只能违反性质4。
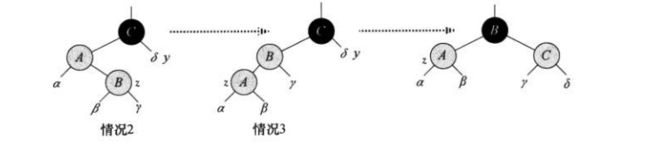
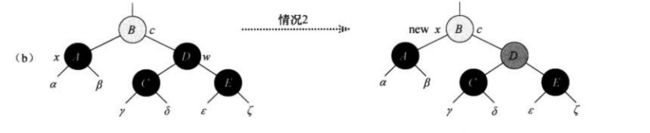
b、情况b:当z.p为z.p.p的左孩子,且叔结点为黑色,z为z.p的右孩子时
情况b中,z为其双亲的右孩子,此时通过左旋变为情况c。z就变为双亲的左孩子,且z与z.p都为红色,所以旋转操作并不影响性质5。并进入情况c。
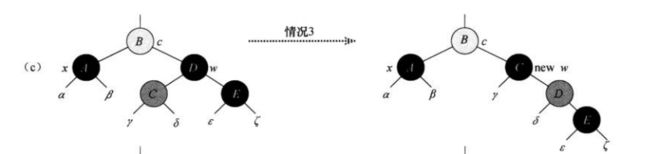
c 、情况c:当z.p为z.p.p的左孩子,且叔结点为黑色,z为z.p的左孩子时
在情况c中,通过改变z的双亲为黑色,z的祖先为红色(此时没有破坏性质5),并以z的祖先做右旋操作,使得树中没有两个相邻的红色结点。下面证明情况b与情况c的循环不定式:
1、情况b让z指向红色的z.p。在情况b与情况c中z的颜色不再改变
2、情况c中让z.p为黑色,如果z.p为根结点,那么下一次迭代一定为黑色的
3、情况b与情况c都保持了性质1、3、5。首先z在情况b与c中不可能为根结点,所以不可能违反性质2。对于违反的性质4、通过情况c的右旋操作使得修正。
e、情况e:当z.p为z.p.p的右孩子,且叔结点为红色时。
情况e与情况a完全对称,所以其维护性质4的操作也相同,这就不赘述了。
f、情况f:当z.p为z.p.p的右孩子,且叔结点为黑色,z为z.p的左孩子时。
同样,情况f与情况b对称,不同的是情况b需执行左旋维持性质5。而情况f需执行右旋操作维持性质5。
g:情况g:当z.p为z.p.p的右孩子,且叔结点为黑色,z为z.p的右孩子时
同样,情况g与情况c对称,执行着色相同,不同的是情况c执行的右旋,而情况g执行的是左旋。
终止: 循环终止的条件是z.p为黑结点,根据上面的分析,进入循环只能是破坏了性质4。那么此时只能破坏性质2。所以z只能是根结点,z.p则为哨兵元素。所以在返回之前,把root着为黑色。
下面给出实现redBlackInsertFixup的伪代码:
redBlackInsertFixup(z) {
// 循环的条件区分是破坏性质2还是性质4
while (z.p.color == RED) {
if (z.p == z.p.p.left) {
y = z.p.p.right;
if (y.color == RED) {
z.p.color = RED; // caseA
y.color = BLACK; // caseA
z.p.p.color = RED;// caseA
z = z.p.p; // caseA
continue; // caseA
} else if (z == z.p.right) {
z = z.p; // caseB
leftRotate(z); // caseB
}
z.p.color = BLACK; // caseC
z.p.p.color = RED; // caseC
rightRorate(z.p.p); // caseC
} else {
y = z.p.p.left;
if (y.color == RED) {
z.p.color = RED; // caseD
y.color = BLACK; // caseD
z.p.p.color = RED;// caseD
z = z.p.p; // caseD
continue; // caseD
} else if (z == z.p.left) {
z = z.p; // caseE
rightRorate(z); // caseE
}
z.p.color = BLACK; // caseF
z.p.p.color = RED; // caseF
leftRorate(z.p.p); // caseF
}
}
// 维护性质2
root.color = BLACK;
}④、删除
红黑树的删除操作删除一个结点同样需要O(lgn)。
1)替换操作
调用redBlackTransplant(u,v)会把结点u的位置替换成结点v。下面给出其实现的伪代码
redBlackTransplant(u,v) {
// 如果u是根结点,那么v成为根结点
if (u.p == sentry)
root = v;
// 如果u是其双亲的左孩子,那么v成为u双亲的左孩子
else if (u == u.p.left)
u.p.left = v;
// 反之,v成为u双亲的右孩子
else u.p.right = v;
// v替换掉u的位置
v.p = u.p;
}2)删除操作
红黑树的删除操作同二叉搜索树。需要考虑三种情况
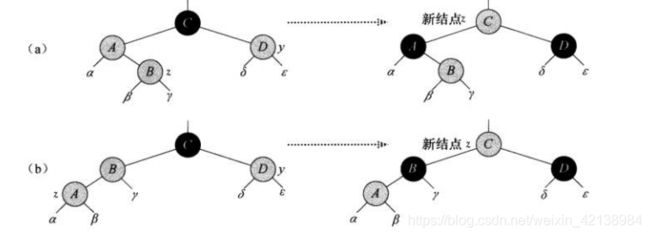
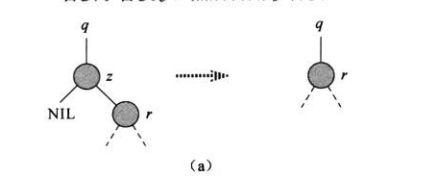
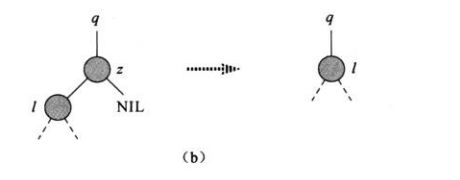
i)当删除的结点没有左孩子时,那么把其替换到删除结点的位置。如图a
ii)如果z仅有一个左孩子,那么把其替换到删除结点的位置。如图b
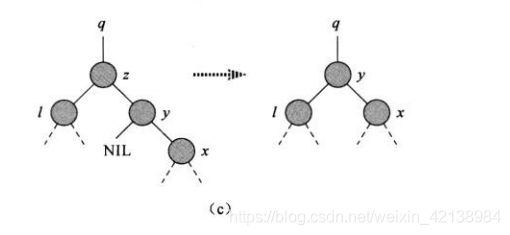
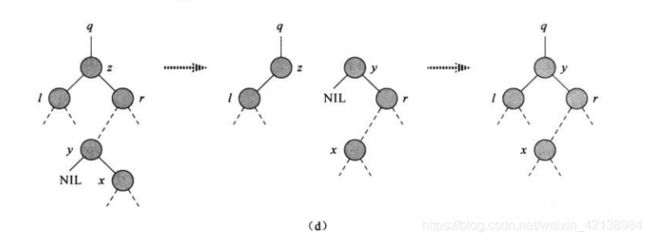
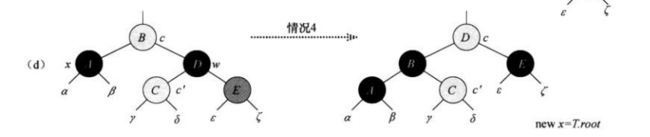
iii)如果z有两个孩子,那么找它的后继元素y。当y为删除结点的右孩子时,那么把y替换到z的位置,如图c。当y不为其右孩子,(注:如果某一结点有两个孩子,那么它的后继元素没有左孩子)x为y的右孩子,此时x替换y,y替换z。如图d。下面是其删除的伪代码
redBlackDelete(z) {
y = z;
// 记录的第一个量,y的原始颜色
y-original-color = y.color;
// 情况1
if (z.left == sentry) {
x = z.right;
redBlackTransplant(z, z.right);
// 情况2
} else if (z.right == sentry) {
x = z.left;
redBlackTransplant(z, z.left);
// 情况3
} else {
y = treeMinimum(z.right); // 找z的后继元素
y-original-color = y.color;
x = y.right;
// 后继元素为z的右孩子时
if (y.p == z)
x.p = y; // 保证y的右孩子始终指向y
// 后继元素不为z的右孩子
else {
// x替换y
redBlackTransplant(y, y.right);
y.right = z.right;
y.right.p = y;
}
// y替换z
redBlackTransplant(z, y);
// z还是联系其孩子,所以使y指向z的孩子
y.left = z.left;
z.left.p = y;
// 把y的颜色着为z的颜色,以此维持红黑性质
y.color = z.color
if (y-original-color == BLACK)
redBlackDeleteFixup(x);
}
}3)维护操作
在删除中,我们需跟踪两个量:一是删除结点或删除结点的后继元素y的原始颜色(因为颜色可能被替换)。二是替换结点y的位置记录结点x。比如说替换结点是:z.left替换z,那么x = z.left记录当前的位置。跟踪这两个量是为了当删除后,维护红色性质。回到代码中,替换y与z替换后,y的颜色变为z的颜色。首先考虑下,如果y的原始颜色为红色时,那么会不会违反红黑性质。答案是不会的。原因如下:
1、性质1:此时树中结点要么是红色,要么是黑色。满足
2、性质2:如果替换的元素z为根结点,那么替换后y为根结点,并且获取了z的颜色。满足
3、性质3:叶子结点还是黑色。满足
4、性质4:y替换z的位置,z没有被替换前满足红黑性质,那么y替换后还是满足。如果y原来为红色,x就必然为黑色,y.p为黑色。所以x替换y位置也必定不会违反红黑性质。满足
5、性质5:y原来为红色,即使y替换了z。在包含y的简单路径上,它的黑高还是不变的。
综上:当y的原始颜色为红色决不会违反红黑性质。
那么看看y原始颜色为黑色会不会违反红黑性质:
1、性质1:此时树中结点要么是红色,要么是黑色。满足
2、性质2:在删除情况1、2中,y为删除结点z。如果y就是原来的根结点,那么它的一个红色孩子结点就会替换它,这将违反性质2。不满足
3、性质3:叶子结点还是黑色。满足
4、性质4:因为y的原始颜色为黑色,那么x与y.p结点都可能为红色。当x替换y之后,那么此时有两个相邻的红结点。不满足
5、性质5:当y替换到z的位置处,那么在包含y的简单路径上将少一个黑色结点,那么黑高将会变化。不满足
综上:当y为黑结点时,将违反性质2、4、5。
*解决思想:想要维护红黑性质,那么把x视为还有一层黑色。比如说,原来x为红结点,那么此时x将既有红色又有黑色。原来x为黑结点,那么此时x就含有两层黑色。但添加的额外黑色是针对x结点它是逻辑上存在,不反映在它的color属性上。此时,红黑树中将不会违反性质5。但却违反了性质1,因为x结点即可以为红色又可以为黑色。所以以下的解决过程都是说明红黑树怎么维护性质1、2、4的
redBlackDeleteFixup()过程中将包含八种情况。在研究每种情况之前,我们还需要说明几点问题:
1)while循环:whilie循环的目标是将额外的黑色延树上移,直到:(注:x进入循环只能是红色,如果x为黑色那么将不会违反红黑性质)
1、由情况a->情况b与情况e->情况f时,x指向红黑结点,将x着为(单个)黑色
2、x指向根结点,此时可以简单地“擦除”额外的黑色
3、执行适当的旋转和重新着色,退出循环
2)变换中保持性质5:
在每种情况中,从子树的根(包括根)到每棵子树α、β、...、ξ之间的黑结点个数(包括x的额外的黑色)并不会被变换改变。因此,如果性质5在变换之前成立,那么在变换之后也成立。比如说,情况a中(图a),在变换前后,根结点至子树α或β之间的黑结点都为3。(结点x添加了一层额外的黑色)类似地,在变换前后根结点至子树γ、δ、ε、ζ中任何一个之间的黑结点数都为2。
3)变换中维护的性质2:
当调用redBlackDeleteFixup时,如果进入情况a,那么会由情况a进入b、c、d中一种情况。
如果情况a->情况b,那么退出循环的条件不可能是x.color == black只能是x== root。因为x.color = red(此时x去掉一层黑色,x.p添加一层黑色)。
如果不进入循环,那么x== root。最后去掉添加的黑色。即满足性质2
如果重新进入循环,此时如果直接进入情况b。又经由情况b退出循环后,(经由上面分析,只有删除情况为1或2时才能破坏性质2)那么此时x一定是root。 所以也满足性质2
如果重新进入循环,此时如果进入了情况c、或d那么x= root。(在执行之前已经去掉x的黑色)。并退出循环,此时root.color = black。所以满足性质2
4)变换中维护的性质4:
为了维护因为x与x.p都为红色结点的问题,通过对结点的着色与旋转解决(下面通过对每种情况分析说明)
a、情况a:当x为其双亲的左孩子,它的兄弟结点w为红色时
在情况a中,因为w的孩子必定为黑色,我们需要经过改变w为黑色,x.p为红色,并经过左旋后。此时,x的新兄弟必定为w的黑色左孩子,因此进入情况b、c、d的一种。此时没有违反任何红黑性质。
b、情况b:当x为其双亲的左孩子,它的兄弟结点为黑色,并且它的两个孩子都为黑色时
因为w的孩子为黑色,并且w也为黑色,那么从x与w去除一层黑色,使得x只有一层黑色而w为红色。为了补偿x与w去掉的黑色,在原来是红色或是黑色的x.p添加一层黑色。并通过x.p作为新结点重复while循环。注意到,如果是因为情况a->情况b的话那么作为下次while循环的新结点x是红黑树的。在最后,将其着为单一的黑色。
(注:浅阴影的颜色是红黑色。)
c、情况c:当x为其双亲的左孩子,它的兄弟结点为黑色,并且它的左孩子是红色,它的右孩子是黑色时
在情况c中通过交换w和其左孩子的颜色,并对w进行右旋。此时由情况c进入情况d。并且这过程不违反任何红黑性质。
d、情况d:当x为其双亲的左孩子,它的兄弟结点为红色,并且它的右孩子是红色时
在情况d中通过对某些颜色进行更改并且对x.p做一次左旋,此时可以去掉x的额外黑色,并且没有破坏任何的红黑性质,在最后x为root退出循环,返回。
e、情况e:当x为其双亲的右孩子,它的兄弟结点为红色时
情况e与情况a对称,不同的是需情况a进行右旋而情况e进行左旋操作
f、情况f:当x为其双亲的右孩子,它的兄弟结点为黑色,并且它的两个孩子都为黑色时
情况f同样与情况b对称。
g、情况g:当x为其双亲的右孩子,它的兄弟结点为黑色,并且它的左孩子是黑色,它的右孩子是红色时
情况g与情况c对称,不同的是情况c需右旋而情况g左旋
h、情况h:当x为其双亲的右孩子,它的兄弟结点为黑色,并且它的右孩子是黑色时
情况h与情况d对称,不同的是情况d需左旋而情况h右旋
下面给出维护删除的伪代码:
redBlackDeleteFixup(x) {
// x为黑色时不会违反任何性质4、5,如果x为根那么就只有删除情况1、2
// 如果x为红色,我们使其变为单一的黑色即可
while (x != root and x.color == BLACK) {
if (x == x.p.left) {
w = x.p.right;
// 当进入情况a时,它可以进入情况b、c、d中的一种
if (w.color == RED) { // caseA
w.color = BLACK; // caseA
x.p.color = RED; // caseA
leftRorate(x.p); // caseA
w = x.p.right; // caseA
}
if (w.left.color == BLACK and w.right.color == BLACK) {
w.color = RED; // caseB
x = x.p; // caseB
continue;
} else if (w.right.color == BLACK) {
w.left.color = BLACK;// caseC
w.color = RED; // caseC
rightRotate(w); // caseC
w = x.p.right; // caseC
}
w.color = x.p.color; // caseD
x.p.color = BLACK; // caseD
w.right.color = BLACK; // caseD
leftRorate(x.p); // caseD
x = root; // caseD
} else {
w = x.p.left;
if (w.color = RED) {
w.color = BLACK; // caseE
x.p.color = RED; // caseE
leftRorate(x.p); // caseE
w= x.p.left; // caseE
}
if (w.left.color == BLACK and w.right.color == BLACK) {
w.color = RED; // caseF
x = x.p; // caseF
} else if (w.left.color == BLACK) {
w.right.color = BLACK;// caseG
w.color = RED; // caseG
leftRorate(w); // caseG
w = x.p.left; // caseG
}
w.color = x.p.color; // caseH
x.p.color = BLACK; // caseH
w.left.color = BLACK; // caseH
rightRorate(x.p); // caseH
x = root; // caseH
}
}
x.color = BLACK; // 擦除额外黑色
}⑤、检索
红黑树的检查操作也可以在O(lgn)时间内完成
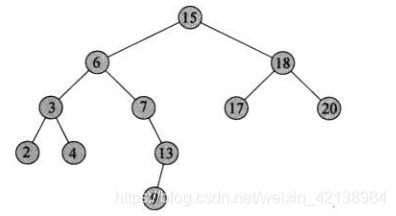
检索根据根结点按照寻找元素的大小条件依次递归直到遇到检索结点等于检索元素。比如说,我们需要检索3号元素,那么一开始从根结点15出发,因为3<15。所以在15结点左子树,此时检索结点x=6。3<6,那么继续往6的左子树查找。此时检索结点为3。所以3=3返回。
下面给出其伪代码:
redBlackTreeSerach(x, key) {
if (x == sentry or x.key == key)
return x;
// 递归找x的右子树
if (x.key < key)
return redBlackTreeSerach(x.right, key);
// 否则找x的左子树
else return redBlackTreeSerach(x.left, key);
}
2、TreeSet
TreeSet被设计用来保存按照某种次序存储元素的集合。它里面没有重复的元素,对于存储的元素需事先Comparable接口。TreeSet采用红黑树作为其存储数据的数据结构。而TreeSet类的设计基于实现红黑树的TreeMap(下面会具体说明)。这也就是说TreeSet存储的元素将由TreeMap存储。
①、TreeSet的类声明
②、TreeSet的关键字段
1)m字段
NavigableMap接口实际是TreeMap实现,其中key为我们存储的元素,value对于所有的元素都是相同。其值为PRESENT
2)present字段
③、TreeSet的构造器
1)接受实现NavigableMap接口参数的构造器
2)自然顺序空的无参TreeSet构造器
该构造器也是默认构造器,它将调用实现NavigableMap接口参数的构造器。为m字段赋值,其实质就是使用TreeMap存储元素
3)接受按照特定排序的Compaortor类型参数的构造器
该构造器,将按照实现Comparator接口的元素并按照其排序算法进行排序。此外它将调用TreeSet的默认构造器
4)自然顺序含有元素的构造器
调用该构造器,它将把Collection中的所以元素放入TreeSet中,并调用默认构造器
5)实现SortedSet接口参数的构造器
同3)号构造器,此时元素将按照特定的排序算法进行排序,并且把SortedMap中的所有元素放入TreeSet中。
④、TreeSet的重要方法
1)add()
在TreeSet中插入一个元素,实际使用TreeMap进行插入,其中key为我们插入的元素,value为一个固定的值PRESNET。
2)remove()
同add,也是根据TreeMap进行删除操作。
总之TreeSet中的所有关于集合的操作都是TreeMap进行操作。
⑤、TreeSet的实现
既然说TreeSet存储数据的结构是红黑树,那么红黑树在TreeMap中是怎么样定义的。
1)、TreeMap使用静态final内部类Entry做为构建红黑树结构
2)、Entry类包含七个字段:如下
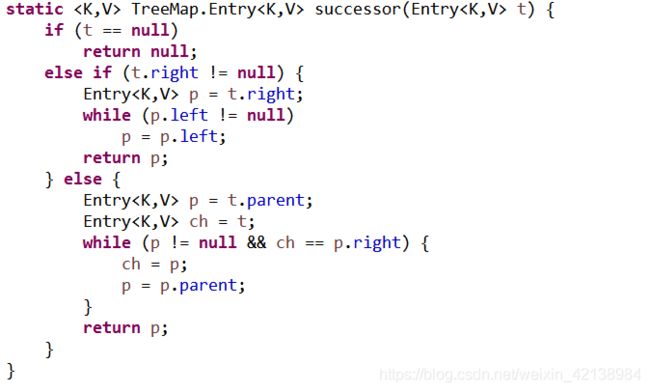
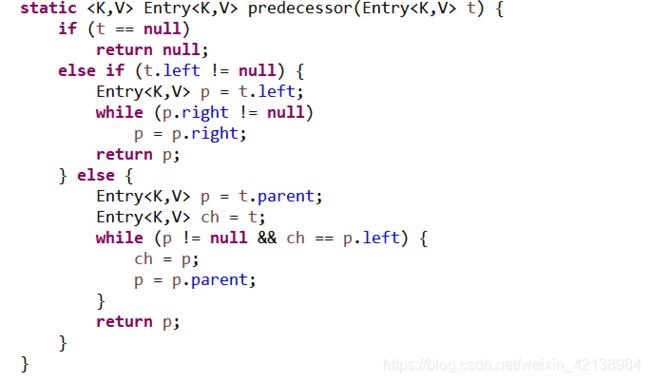
3)、Entry类中红黑树搜索前驱与后继的源码如下:
4)、Entry类中红黑树的左旋与右旋操作如下:
更多介绍请看我TreeMap的那一章。
三、基于散列表实现 —— HashSet
注:附录B为我手写的散列表,其中一个是基于链接法解决冲突的散列表,另一个是基于开放寻址法解决冲突的散列表
1、散列表
散列表是普通数组概念的推广。普通数组可以直接寻址,使得能在O(1)时间内访问数组中任何一个元素。但是当实际存储的关键字小于可能的全部关键字时,那么直接寻址的空间浪费率就会很高。此时采用散列表就成为直接寻址表的一个很好的替代。散列表并不是把关键字作为下标进行检索,而是根据关键字进行计算相应的下标。
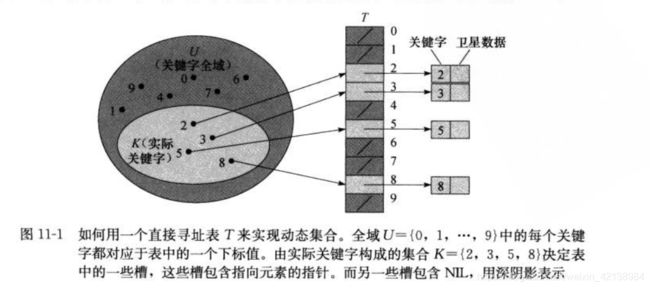
①、直接寻址表
令全域U={0,1,...,m-1}共有m个关键字。直接寻址表也可称为数组,记为T[o..m-1],其中每个位置称为槽,它对应全域U中一个关键字。槽k指向集合中一个关键字为k的元素。如果该集合没有关键字为k的元素,则T[k] = null。如图所示
采用直寻表最大的坏处是,当全域U很大,则在计算机内存放入容量为U的一张表示不实际的。特别的,当实际需要的关键字集合K比全域U小很多的时候,使得分配给U的大部分空间都将浪费。
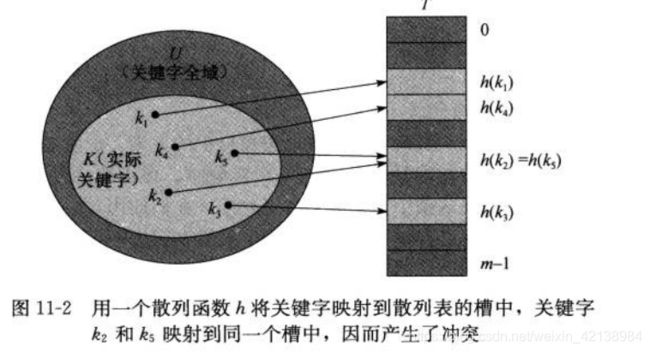
②、散列表
在直接寻址下,具有关键字k的元素被存放在槽k中(如上图所示)。在散列表中,该元素存放在槽h(k)中;即利用散列函数,由关键字k计算出槽的位置。通过由函数h将关键字的全域U映射到散列表T[0..m-1]的槽位上:
这里,h(k)为关键字k的散列值。如下图:
散列表能很好的利用分配给它的空间,使得我们所有的关键字k都能有存储空间。但是有一个致命的问题,就是散列函数h的设计,一个不好的散列函数使得我们可能有超过两个以上的关键字映射到同一个槽位上。这将产生“冲突”问题。
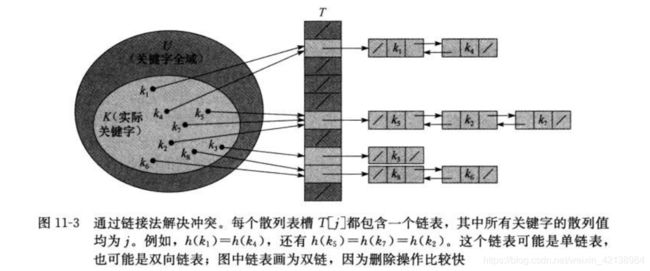
1)链接法解决冲突问题
在链接法中,每个槽位上存储了null或者链表的表头指针,通过把散列在同一个槽位上所有元素放在一个链表j中。
i)装载因子(load factor)α
定义:给定一个能存放n个元素、具有m个槽位的散列表T中,装载因子α为n/m,即一个链的平均存储元素数。假定,任何给定的一个元素等可能地分布到m个槽位中的一个,这个假设称为简单均匀散列。
定理1:在简单均匀散列的假设下,对于用链接法解决的冲突的散列表,一次不成功的查找的平均时间为O(1+α)(证明请看《算法导论第三版》p145-p146)
定理2:简单均匀散列的假设下,对于用链接法解决的冲突的散列表,一次成功的查找的平均时间为O(1+α)(证明请看《算法导论第三版》p146)
总结:当散列表中槽数至少与表中的元素数成正比时,那么n=O(m),即α=n/m=O(m)/m=O(1)。所以当链表采取双向链表时,插入、删除、检索都可以在O(1)时间内完成。
ii)链接法的插入操作
链接法的插入能在O(1)时间内完成,插入过程将完成以下几件事:通过散列函数计算出关键字k的散列值;找到散列表中存储位置槽j;如果槽j未插入元素,那么把关键字k插入进去;否则,找到槽j中链表的最后一个位置,在进行插入。其为代码如下:
chainInsert(k) {
// 获取关键字k在链接表的位置
serachNode = T[hashCode(k)];
// 如果当前位置已经连接了元素,那么不断轮询,直到能插入的位置
if (serachNode != null) {
while (serachNode.next != null)
serachNode = serachNode.next;
serachNode.next = k;
k.pre = serahNode;
} else
T[hashCode(k)] = k;
}
iii)链接法的删除操作
同样链接法的删除能在O(1)时间完成,删除过程将完成以下几件事:通过散列函数计算出关键字k的散列值;找到散列表中存储位置槽j;如果槽j中第一个链表元素恰好为查找元素,那么删除其引用,否则,继续轮询链表直到找到元素位置,解决该元素的连接。下面是其伪代码:
chainDelete(k) {
// 当k的散列值的槽位没有元素,那么抛出错误
if (T[hashCoed(k)] == null)
error: "initalize LinkedList"
else {
node = T[hashCode(k)];
while (node.next != null)
if (node.key == k)
break;
node = node.next;
// 退出循环时,首先得判断是不是找到的node
if (node.key != k)
error: "no such key on chain hash table"
// 当找到的node为链表一个元素时
if (node.pre == null) {
node.next.pre == null;
T[hashCode(k)] = node.next;
} else
node.pre.next = node.next;
// 当node为最后一个元素时
if (node.next == null)
node.pre.next = null;
else
node.next.pre = node.pre;
}
}iv)链接法的检索操作
链接法的检索操作同样可以在O(1)时间内完成。它的操作与删除操作类似:通过过散列函数计算出关键字k的散列值;找到散列表中存储位置槽j;如果槽j中第一个链表元素恰好为查找元素,那么返回它,否则,继续轮询链表直到找到元素位置,随后返回查找的元素。下面是其伪代码:
chainSerach(k) {
// 当发现查找的关键字在槽位上没有,那么报错
if (T[hashCode(k)] == null)
error: "initalize LinkedList";
node = T[hashCode(k)];
while (node != null && node.key != k)
node = node.next;
// 当找到的元素为空时,则报错
if (node == null)
error: "No such Key";
else
return node;
}2)开放寻址法解决冲突问题
在开放寻址法中所有的元素将放在散列表中,它不像链接法,每个槽位不会存储链表表头的指针。也就是说:每个槽位或者为关键字或者为null。当查找某个元素时,要系统地检查所有的表项,直到找到所需的元素。
因此,开放寻址法中,散列表可能将会被填满,以至于不能插入新元素。因此我们的装载因子α不能大于1。开放寻址法的好处是不用多余的空间存储指针,使得可以用同样的空间提供更多的槽,潜在地减少了冲突,提高了检索速度。
i)探查序列
使用开放寻址法插入一个元素,需要连续的检查散列表,这称为探查(probe),直到有空的位置能放入带插入的关键字位置。
探查序列是由散列函数扩充产生,对每一个关键字k,使用开放寻址法的探查序列(probe sequence)为:
探查函数定义如下:
因此对于插入、删除、检索将依靠这个探查序列探查到是否有符合的条件。探查号将从0开始直到m-1,依次检查散列表中的表项是否有符合的条件。
ii)开放寻址法的插入操作
开放寻址法的插入操作:它将根据探查函数的值作为散列表的下标查找对应的元素是否为空,若为空则返回,若不为空,那么继续下次探查此时探查号值增1直到找到这个元素或者探查号为m-1。其伪代码如下:
openAddressInsert(k) {
i = 0;
do {
j = h(k, i);
if (T[j] == null)
T[j] = k;
return ;
else i = i + 1;
} while (i ! m - 1)
error: "hash table overflow";
}iii)开放寻址法的删除操作
开放寻址法的删除和插入类似,通过探查序列找到需要删除的元素。但有一个问题,因为探查函数是根据上一个关键字的值来进行搜索下一个槽位。此时,如果将槽i的关键字删除,那么经过槽i搜索的下一个槽位将无法检索到。所以,我们删除元素时,需要人为的设置这个槽位为"Delete"替代原来的null标记该槽位空。(当然,插入操作也需要检索这个关键字“Delete”)。下面是其实现的伪代码:
openAddressDelete(k) {
i = 0;
do {
j = h(k, i);
if (T[j] == k)
// 当找到元素后,标记它为delete
T[j] == "Delete";
return ;
else i = i + 1;
} while (i != m - 1)
error: "no such";
}iv)开放寻址法的检索操作
开放寻址法的检索操作很简单:通过探查序列找到元素后直接返回。下面是它的伪代码:
openAddressSerach(k) {
i = 0;
do {
j = h(k, i);
if (T[j] == k)
return T[j];
i = i + 1;
} while (i != m -1)
error: "no such"
}v)探查函数的选择
假设:每个关键字的探查序列等可能地为<0, 1, ... , m-1>的m!中排序中的任一种称为均匀散列(uniform hashing)。均匀散列是前面的简单均匀散列概念一般化,它的结果是一个探查序列,而不是一个数。
a、线性探查:
给定一个普通的散列函数h': U->{0, 1, ... , m-1},称它为辅助散列函数,线性探查方法采用的散列函数为:
线性探查很容易实现,它的探查槽位顺序为:T[h'(k)]、T[h'(k) + 1]、... 、T[m-1]、...、T[0]、T[1]、...、T[h'(k)-1]。但线性探查存在一个问题,称为一次群集。当连续被占用的槽不断增加,平均查找时间也随之增加,此时元素的群集现象将很容易出现,这是因为一个空槽前有i个满的槽时,该空槽下一个将被占用的概率是(i+1)/m。
b、二次探查
二次探查将使用如下形式的散列函数:
其中h'为辅助散列函数,c1、c2为正的辅助常数,i=0,1,... ,m-1。初始探查探查的位置T[h'(k)],后续的探查位置要加上一个一个偏移量,该偏移量以二次的方式依赖于探查序号i。
二次探查看似加上一个偏移量就可以很好解决群集现象。但是,如果两关键字的初始探查位置相同,那么它们的探查序列也是相同的,这是因为h(k1,0)=h(k2,0)有h(k1,i)=h(k2,i)。这一性质将导致轻度的群集,称为二次群集。
c、双重散列
双重散列采用如下形式的散列函数:
其中,h1、h2均为辅助散列函数。初始探查位置为T[h1(k)],后续的探查位置时前一个位置加上偏移量h2(k)模m。因此,双重散列更依赖关键字k,因为初始探查位置,偏移量或者二者都会发生变化。因此它是用于开放寻址法最好的探查函数之一。
3)一个好的散列函数设计
在前面介绍的链接法与开放寻址法都依靠散列函数对关键字的检索。那么一个好的散列函数应该满足以下特点:一是对于每一个关键字都能等可能地散列到m个槽位中的任何一个,并与其它关键字以散列到哪个槽位无关。二是对于不是自然数的关键字都有办法转化为自然。
i)除法散列法
在除法散列法中,通过取k除以m的余数,将关键字k映射到m个槽位中的任何一个,散列函数为:
假设,如果散列表的大小m=12,关键字k为100,所以h(k)=4。
ii)乘法散列法
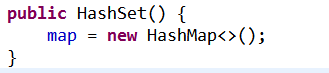
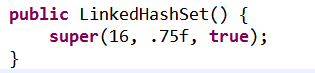
乘法散列法需要进过两个步骤:一是用关键字乘上常数A(0 HashSet是基于散列表实现的数据结构,为快速检索而存在的结构。同TreeSet是基于TreeMap实现,HashSet是基于HashMap实现。 ①、HashSet的类声明 ②、HashSet的字段 1)map字段 map是HashMap类型的,它的key即为HashSet存储的值,value为常量。 2)present字段 present字段作为在map中存储的常量value ③、HashSet的构造器 1)无参构造器 调用HashSet无参构造器,将会创建一个固定容量的HashMap。 2)含有元素接受Collection参数的构造器 向map中添加Collection中的所有元素,其中HashMap的初始化容量为Collection.size() / 0.75 + 1 3)自设初始化容量与负载因子大小的构造器 4)自设初始化容器的构造器 5)包私有构造器 该构造器是供HashSet的子类LinkedHashSet调用。 ④、HashSet的重要方法 1)add() 在HashSet的add方法中,也说明了:HashSet不是存储元素结构而是采用HashMap作为实际存储元素。其中HashMap的key为存储的元素,value为一个常量字段。 2)remove() 同add方法,删除元素也是由HashMap实现。 ⑤、HashSet的实现 HashSet实现真正是HashMap,HashMap采取键值对存储元素,其中数据结构为散列表。那么在HashMap怎么实现散列表? 1)结点的定义 。。具体分析情况我的HashMap哪一章 如果说TreeSet,HashSet的实现都是根据TreeMap,HashMap。同样LinkedHashSet也是基于LinkedHashMap实现。LinkedHashSet是具有双向链的散列表结构。在HashMap的Node结点的定义中,只给出了链接表的单向链实现。那么在LinkedHahsSet中实现了链表的双向链接。 在HashMap中元素迭代时是无序,它并不是按照我们元素的插入的顺序,而是按照散列表的位置顺序进行迭代。而LinkedHashMap中元素的迭代可以保证按照元素的插入顺序进行。虽然在性能上不如HashMap,但它解决了HashMap元素的迭代顺序问题。 LinkedHashSet类中的代码量很少,它继承自HashSet,它有4个构造器。 1、LinkedHashSet无参的构造器 无参的构造器将调用HashSet的包私有构造器,将为HashSet的map字段引用一个LinkedHashMap实例。 2、LinkedHashSet设置散列初始容量构造器 通过设置LinkedHashMap的初始容量创建一个LinkedHashMap 3、LinkedHashSet设置散列初始容量与负载因子大小构造器 同样,设置LinkedHashMap散列表的初始容量与负载因子的大小创建一个LinkedHashMap 4、LinkedHashSet接受Collection进行元素填充 调用该构造器将创建一个具有2*Collection.size()或者11大小初始容量与0.75负载因子大小的LinkedHashSet。并且把其元素填充到LinkedHashMap中。 此外LinkedHashMap详细介绍请看我相关章节。 equals方法作为Object类中设计用于扩展的方法,它声明了两个对象是否具备等价关系。它不同于“==”操作符,当使用“==”操作符比较两个对象时,比较的是它们地址,也就是说两个对象为同一个对象时它才能为真。而equals方法中,只要两个对象是同一个对象或者它们两个的关键域是相等的,那么可以说这两个对象具有等价关系。 equlas方法使用最多的就是集合中,在集合中放入的元素必须复写equals。以确保对象在集合中的“唯一性”(Map与Set中存储的元素必须重写)。比如说,在红黑树中我们查找某个元素,如果存入的元素没有重写equals方法。那么将会发生:明明已经插入,却查询不到元素。这是因为查询的元素与存入的元素没有实现“逻辑”相等的功能。 ①、equals方法的声明 下面为Object类中,equals方法: 该方法接受一个Object类型的参数,并返回布尔值。 ②、equals方法在什么情况下不需要被重写 1)类的每个实例本质上都是唯一的。 2)类是否提供了“逻辑相等”的测试功能。 3)超类已经覆盖了equals,那么子类无需在复写equals。 4)类是私有的或是包私有,此时equals将永远不会被调用。 ③、equals方法的通用约定 在Object类中对equals做出如下几点通用规定,以确保equals能得到正确的结果 1)自反性(reflexive):对于任何非null的引用值x,x.equals(x)必须返回true 2)对称性(symmetric):对于任何非null的引用值x和y,当且仅当y.equals(x)返回true时,x.equals(y)必须为true。 3)传递性(transitive):对于任何非null的引用值x、y和z,如果x.equals(y)返回true,并且y.equals(z)也返回true,那么x.equals(z)也必须返回true 4)一致性(consistent):对于任何非null的引用值x和y,只要equals的比较操作在对象中所用的信息没有被修改,多次调用x.equals(y)就会一致地返回true,或者false 5)非空性(non-nullity):对于任何非null的引用值x,x.equlas(null)必须返回false 尽管通用约定看似夸张,但是我们违反其中一条,将会造成不可预料的后果。(详情解释请看《Effective Java》第二版第8条)。 ④、怎么编写一个正确高质量的equals方法 1)使用“==”操作符检查“参数是否为这个对象的引用”。若是则返回true。 2)使用instanceof操作符检查“参数是否为正确的类型”。如果不是则返回false。“正确的类型”指equals方法所在的那个类。 3)把参数转换为正确的类型。在转换之前因为会进行类型测试所以会成功 4)对于该类中每个“关键域”,检查参数中的域是否与该对象中对应的域相匹配。对于基本类型的关键域那么使用“==”操作符比较;若是引用类型那么还是通过该引用类型的equals进行比较。 5)覆盖equals时总要覆盖hashCode 6)不要将equals声明中Object对象替换成其他的类型 下面是一个正确高质量的equals方法的编写: hashCode方法用于产生元素的散列码,只要我们覆盖了equals方法,那么必须也要覆盖hashCode方法。在那些基于散列表的集合中,如果我们不这样做的话,从而导致两个等价的对象具有不同的散列码,那么这些集合(hashSet、hashMap等)将无法正常工作。 ①、hashCode的方法声明: 上图为Object类中hashCode方法的声明。hashCode方法不接受任何参数,返回整型值。 ②、hashCode的通用约定 同equals方法,hashCode在Object类中也做出如下几点约定: 1)在程序执行期间,只要对象的equals方法的比较操作所用到的信息没有被修改,那么对这同一个对象调用多次hashCode方法都必须始终如一地返回同一个整数。 2)如果两个对象根据equals(object)方法比较是相等的,那么调用这两个对象中任意一个对象的hashCode方法都必须产生同样的结果 3)如果两个对象根据equals(object)方法比较是不相等的,那么调用这两个对象中任意一个对象的hashCode方法,则不一定要产生不同的整数结果。 对于如果不编写hashCode方法,那么必然违反第二条的规定。两个截然不同的实例上通过equals方法证明这两个实例存在“逻辑相等”,但是对于Object类来说它们两个仅仅是没有任何共通的对象。因此那些使用散列码的集合也必然不能正常的工作。 ③、java中如何编写一个高性能的散列函数 在前面介绍散列表的时候也说过,一个好的散列函数能使我们的元素均匀分布在散列表的每个槽位,使得散列表利用率达到最高,性能最好。但是我只是简单的介绍了两种散列函数的构造。在java中还有另外一种构造高效率的散列函数: 1)把某个非零的常数值,比如17,保存在名为result的int类型变量中 2)对于对象中每个关键域f(特指equals涉及到的每个域),完成以下步骤: a、为该域计算int类型的散列码c: i、如果该域是boolean类型,则计算(f?1:0) ii、如果该域是byte、char、short或int,则计算(int)f iii、如果该域是long类型,则计算(int)(f ^(f >>> 32)) iv、如果该域是folat类型,则计算Folat.floatToIntBits(f) v、如果该域是double类型,则计算Double.doubleToLongBits(f),然后按照步骤2.a.iii计算long类型的整型值 vi、如果该域是引用类型,则调用改域的hashCode。如果改域为null,则返回0 vii、如果该域是数组,则把数组中的每一个元素当做单独的域处理,递归的调用上述规则。 b、根据公式:result = 31 * result + c,把通过步骤a的散列码合并到result中。 3)返回result。 下面是一个正确编写的散列函数。(注:在HashMap还会通过mod槽位数,把每一个元素放入散列表中) compareTo方法是Comparable接口中唯一的方法。comparaTo方法允许进行简单的等同性测试(上面的equals就是一个等同性测试),而且允许执行顺序比较,并且它还可以接收泛型。当某个类实现了Comparable接口,就表明它的实例具有内在的排序关系(或按照字母顺序、数值顺序、甚至时间顺序等)。 在集合中依赖于有序关系的集合要求存储的对象实现Comparable接口,如TreeSet、TreeMap,与那些包含内置排序算法的Collections与Arrays也要求传递的元素实现Comparable接口。假设集合中存储了没有重写的compareTo方法元素,那么这个集合将无法正常的工作,因为检索、插入、删除全是依靠compareTo进行元素的比较,判断到树的那个方向进行检索。 ①、compareTo方法的声明 compareTo在Comparable接口的声明,它接受泛型参数,并返回整型值。 ②、compareTo的通用约定 同equals与hashCode方法,compareTo在Comparable接口也有通用约定。给定符号sgn,它为数学中的符号函数只能返回1、0、-1。 1)自反性:对于所有的x和y都满足sgn(x.compareTo(y)) == -sgn(y.compareTo(x))。 2)传递性:对于所有的x、y和z的比较关系是可传递的:sgn(x.compareTo(y))> 0 && sgn(y.compareTo(z))> 0,那么sgn(x.compareTo(z))> 0 3)对称性:当sgn(x.compareTo(y))== 0暗示着所有的z都满足sgn(x.compareTo(z)) == sgn(y.compareTo(z)) ③、编写正确的compareTo方法 在compareTo的通用约定也包含了较多的数学运算,但这并不妨碍我们有规律的编写正确的compareTo方法。在equals中,比较的对象只能是同一个类或者它的子类,而compareTo可以跨类比较。下面给出其规则: 1)对于整型,通过“<”、“==”、“>”操作符进行比较 2)对于浮点型,通过Float.compareTo()或Double.compareTo()比较 3)对于引用类型,那么递归比较该引用类型的关键域。如果引用类型没有实现Comparable接口,则可以同过构建Compartor进行比较 4)对于数组,通过把每一个数组元素按照上述规则进行比较。 5)对于比较关键域的顺序,应比较最关键的域,如果产生非零值则返回。否则,比较次关键域,依次类推。 逐个比较的compareTo方法 不指定返回值的compareTo方法 三元运算符不指定返回值的compareTo方法 ④、comparator接口 对于那些没有实现Comparable接口的类,或者实现的类比较方式不喜欢。都可以通过创建实现Comparator接口单独的类,编写定制的compareTo方法。Comparator接口包含两个方法:equals与compare方法。当然,我们可以选择不实现equals方法。 下面是Comparator中对compare声明: 传递两个泛型参数,并返回一个整数值 当我们编写了定制的Comparator接口时,应该把它实例化并传递给容器的构造器或者Arrays或Collections中。依次构建定制的compareTo方法。如下:2、HashSet
四、内部链表的散列表 —— LinkedHashSet
五、equals、hashCode、compareTo方法
1、equals方法
public boolean equals(Object o) {
if (o == this)
return true;
if (!(o instanceof PhoneNumber))
return false;
PhoneNumber pn = (PhoneNumber) o;
return pn.areaCode == areaCode
&& pn.prefix == prefix
&& pn.lineNumber == lineNumber;
}2、hashCode方法
![]()
public int hashCode() {
int result = 37;
result = 31 * result + areaCode;
result = 31 * result + prefix;
result = 31 * result + lineNumber;
return result;
} 3、compareTo方法
public int compareTo(PhoneNumber pn) {
// areaCode为整型(通过>或<比较),并且使最关键的域
if (areaCode > pn.areaCode)
return 1;
if (areaCode < pn.areaCode)
return -1;
if (prefix > pn.prefix)
return 1;
if (prefix < pn.prefix)
return -1;
if (lineNumber < pn.lineNumber)
return 1;
if (lineNumber > pn.lineNumber)
return -1;
// 所以比较完后,没有返回。说明这两个对象是相等
return 0;
}public int compareTo(PhoneNumber pn) {
int areaCodeDiff = areaCode - pn.areaCode;
if (areaCodeDiff != 0)
return areaCodeDiff;
int prefixDiff = prefix - pn.prefix;
if (prefixDiff != 0)
return prefixDiff;
int lineNumberDiff = lineNumber - pn.lineNumber;
if (lineNumberDiff != 0)
return lineNumberDiff;
return 0;
}public int compareTo(PhoneNumber pn) {
return areaCode != pn.areaCode ? areaCode - pn.areaCode :
(prefix != pn.prefix ? prefix - pn.prefix : (
lineNumber != pn.lineNumber ? lineNumber - pn.lineNumber : 0));
}![]()
public class TestComparator {
private int value;
private static Random random = new Random(47);
public TestComparator(int value) {
this.value = value;
}
final static class comparatorType implements Comparator
附录A
附录B