python实现HMM做中文分词-----有监督模型

隐马尔科夫模型的简单介绍：

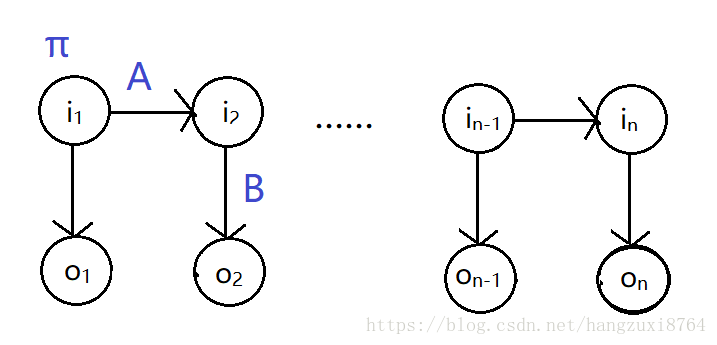
五个元组：
1、初始化π
2、状态转移矩阵 A _NN (N为所有可能的状态q数)
3、观测概率分布 B _NM（M为所有可能的观测值）
4、观测值序列 O {o₁,o₂……o_T}
5、状态值序列 I {i₁,i₂……i_T}

以中文分词为例

---

状态值的取值有四个{B,E,M,S}
B: begin 起始词
E：end 结尾词
M: middle 中间词
S：siggle 单个词
观测值则为要分词的句子，例：你和你那些本不属于这里的行李

---

其中的参数集合为λ=（A,B,π）
状态转移矩阵A：a_ij=P(i_t+1=q_j | i_t=q_i) 是在时刻t处于状态q_i的条件下，时刻t+1转移到状态q_j的概率。如第一个词的状态值是B，第二个词的状态分别为B,E,M,S的概率就是（a₀₀,a₀₁,a₀₂,a₀₃）。

观测概率矩阵B：b_ik=P(o_t=v_k | i_t=q_i) 是在时刻t出去状态q_i的条件下生成观测v_k的概率。

π是初始状态概率：π_i 是第一时刻状态q_i的概率。

HMM的三个基本问题：
1、概率计算问题
已知模型λ=（A,B,π）和观测序列 O {o₁,o₂……o_T}，计算在模型λ下观测序列出现的概率P(O|λ)。
2.学习问题：
已知观测序列 O {o₁,o₂……o_T}，求可以使观测序列P(O|λ)最大的λ=（A,B,π）参数。
3.预测问题：
已知模型λ=（A,B,π）和观测序列 O {o₁,o₂……o_T}，求给定观测序列条件概率P(I|O,λ)最大的序列I。

在有监督的分词中，我们要解决的是问题一（前向概率-后向概率）和问题三（Vertibi），

1.前向概率：
给定参数λ，定义 到时刻t的观测序列为o₁,o₂……o_t 且状态为q_i的概率为前向概率。
（给定参数λ，求1~t时刻的观测序列为o₁,o₂……o_t ，同时t时刻状态为i的概率）
α_t(i)=P(o₁,o₂…… o_t，i_t=q_i|λ)
由此可得，α_T(i)=P(o₁,o₂…… o_T，i_T=q_i|λ)
T时刻状态的可能性有N种，把每种状态下的前向概率加和，就可以得到
P(O|λ)=Σ_iα_t(i)

初值：α₁(i)=P(o₁,i₁=q_i|λ)
其实就是第一时刻，状态值为i的概率π_i(因为是初始时刻)观测值为o₁的概率：π_ib_io1

递推：α_t+1(i)={Σ α_t(j)α_ji}b_iot+1

后向概率：
给定λ，定义到时刻t状态为q_i的前提下，从t+1到T的观测序列为o_t+1,o_t+2……o_T的概率为后向概率。
β_t(i)=P(o_t+1,o_t+2…… o_T | i_t=q_i , λ )
有此可得，α_T(i)=P(o₁,o₂…… o_T，i_T=q_i|λ)
(公式之后还会补充的……)

---

简单的原理已经介绍完了，下面开始代码部分

1,用分好词的训练模型计算参数λ

#读取训练文本
f = file(".\\pku_training.utf8")
data = f.read()[3:].decode('utf-8')
f.close()
tokens = data.split('  ')
#len(data)=4065424  #文章长度
#len(tokens)=1109948 #分词长度

#对参数进行初始化 初始化状态 π，状态转移矩阵A，观测概率矩阵B
pi = [0] * 4   # 隐含状态有四个取值{B:0,M:1,E:2,S:3}
a = [[0] * 4 for x in range(4)]     # a[i][j]：从i状态转移到j状态的概率
b = [[0]* 65536 for x in range(4)]  # b[i][o]：从i状态到o观测值的概率
    
# 开始训练
last_q = 2 #初始化第一个词的状态是从E（2）开始转移

for k, token in enumerate(tokens):
    #对token进行洗涤
    token = token.strip() 
    n = len(token)
    if n <= 0:
	    continue
    
    #如果词的长度为1，则它的状态是S：3
    if n == 1: 
	    pi[3] += 1 
		a[last_q][3] += 1   # 从last_q状态转移到S的数量+1
	    b[3][ord(token[0])] += 1 #ord()函数是对token[0]字符取unicode数值
								 #状态为S 观测值为token的数量+1
	
     #如果n>1,则这个token包含一个B，E，如果还有多余词则包含n-2个M
     #状态B+1，状态E+1，如果n>2,则状态M+n-2
     pi[0] += 1
     pi[2] += 1
     pi[1] += (n-2)
        
     # 状态转移矩阵
     a[last_q][0] += 1
     last_q = 2
     #n==2,意味着这个token的状态是BE，则a[0][2]+1
     if n == 2:
	     a[0][2] += 1
     #n>2,意味着这个token的状态是BMME,其中的M数是n-2
     else:
	     a[0][1] += 1
	     a[1][1] += (n-3)
	     a[1][2] += 1
    
    # 发射矩阵
    b[0][ord(token[0])] += 1 #状态是B，观测值是token[0]的数量+1
    b[2][ord(token[n-1])] += 1 #状态是E，观测值token[n-1]的数量+1
    for i in range(1, n-1): #状态是M，观测值token[i]的数量分别都+1
	    b[1][ord(token[i])] += 1
    # 对概率取log值
    log_normalize(pi)
    for i in range(4):
        log_normalize(a[i])
        log_normalize(b[i])
    return

由此我们能看出，初始化状态概率π是各状态值在的出现概率，即π_i=p(i)