【韩松博士毕业论文】Efficient methods and hardware for deep learning

参考链接：https://blog.csdn.net/weixin_36474809/article/details/85613013

参考链接：https://blog.csdn.net/Uwr44UOuQcNsUQb60zk2/article/details/78334036

---

韩松Deep compression论文讲解——PPT加说明文字

https://blog.csdn.net/weixin_36474809/article/details/80643784

一、摘要

意义

模型压缩一直是机器学习的一个重要方向，并且一个模型不可能只在GPU和服务器上运行才可以。只有通过硬件化实现才能落地。但是神经网络也是非常耗费存储和耗费运算的。本文希望通过一些方法把原本耗费大量存储和运算的神经网络实现在硬件上。

方法

本文采用的方法是剪枝，权值共享和权值量化，还有哈夫曼编码的方法。

剪枝就是去掉一些不必要的网络权值，只保留对网络重要的权值参数；
权值共享就是多个神经元见的连接采用同一个权值，权值量化就是用更少的比特数来表示一个权值。
对权值进行哈夫曼编码能进一步的减少冗余。

作用

作者在经典的机器学习算法，AlexNet和VGG-16上运用上面这些模型压缩的方法，在没有精度损失的情况下，把AlexNet模型参数压缩了35倍，把VGG模型参数压缩了49倍，并且在网络速度和网络能耗方面也取得了很好的提升。

二、方法

2.1 剪枝

在初始化训练阶段后，我们通过移除权重低于阈值的连接而实现 DNN 模型的剪枝，这种剪枝将密集层转化为稀疏层。第一阶段需要学习神经网络的拓扑结构，并关注重要的连接而移除不重要的连接。然后我们重新训练稀疏网络，以便剩余的连接能补偿移除的连接。剪枝和再训练的阶段可以重复迭代地进行以减少神经网络复杂度。实际上，这种训练过程除了可以学习神经网络的权重外，还可以学习神经元间的连通性。这与人类大脑的发育过程 [109] [110] 十分相似，因为生命前几个月所形成的多余突触会被「剪枝」掉，神经元会移除不重要的连接而保留功能上重要的连接。

相对位置的参数：在压缩完参数之后，我们存了权值和权值对应的参数。之前的参数存的是绝对的参数，我们现在存相对的参数，就是两个参数的差值，比如我们用三个特存相对的参数，只要两个元素的距离小于8，都能把参数存为3个比特的，如果两个参数的距离大于这个值，我们就在第8个位置设置一个0值。

通过CSC得到了压缩的矩阵，可以通过差分存储进一步压缩存储数量。例如我们想用三比特的值来存储相应的Index。

3bit可以容忍的间距为8

当间距小于8时：用3比特的值就可以恢复出相应的位置。
当间距大于8时：在第8个位置插入0值，然后用3bit的与插入的0值的差分位置恢复出相应的位置。
间距大于8的倍数时：每隔8个位置插入0值，与最后一个0值的3bit的差分位置恢复出位置。

2.2 权值量化与共享

2.3 初始化权重的值

权值共享的是聚类中心点的位置，初始的聚类中心点是如何确定的呢？有三种方法可以确定聚类中心点的位置。一是随机的方法，就是在权值中随机的选k个值做为聚类中心点。还有一种是基于密度的初始化，我们可以看这个图，横轴是对应的权值的值，纵轴是权值的数量，类似于直方图一样。红色的线是权值的直方图统计，蓝色的线是权值的累积统计，类似于概率密度函数和概率累积函数。基于密度的初始化就是把权值从小到大等分成k份，然后每一份分界点的权值就是聚类的中心。线性的初始化就是直接把最小值最大值之间直接线性进行划分。

因为网络中大的权值往往是更重要的，前两种方法容易让聚类的中心点往概率密度大的地方累积，而线性分类法权值更容易是大的。所以线性的初始化方法比较好，通过后面的实验，也发现通过线性的分类方法取得了更好的准确率。

2.4 哈夫曼编码

哈夫曼编码运用字符出现的概率来进行编码，只要不是均匀分布的，哈夫曼编码就能减少一定的冗余，比如在AlexNet中，相应的权值的直方图和权值参数的直方图是上面这两种，用哈夫曼编码可以减少20-30%的信息冗余。

三、实验

首先第一个实验，不同压缩方法在不同压缩率下精度的损失。横轴是压缩率，越靠左压缩率越大，纵轴是精度的损失，就是压缩之前和压缩之后的准确率的减少的量。这条曲线越靠左上越好，表明更大压缩率下精度损失更少，我们看到最好的方法就是剪枝和权值共享和权值量化的方法。

然后就是权值共享过程中，聚类的初始化值对实验结果的影响，三条曲线分别是上面讲到的三种不同的聚类方法。横轴是压缩的比特数，越靠左表明压缩的比率越大，纵轴是准确率，表明随着压缩的越来越少的比特数，精度越来越低，所以曲线越靠上越好。效果最好的是红色的这条线，就是我们初始聚类初始化的时候，采用线性初始化的方法能达到最好的效果。

下面这三个图表示不同的压缩率对不同层的影响，第一个是压缩的比特数对全连接层的影响，第二个是压缩的比特数对卷积层的影响，第三个是两个层的压缩比特数对实验结果的影响，我们发现卷积层比全连接层对压缩的比特数更加敏感。

然后就是相应的实验，AlexNet压缩了35倍，把VGG压缩了49倍，相比其他的压缩方法，作者的方法没有精度损失并且达到了最大的压缩率。

---

韩松DSD:Dense-sparse-dense training for deep neural networks论文

https://blog.csdn.net/weixin_36474809/article/details/85322584

一、摘要

贡献点：

1.1 全新模型

提出了一个全新的DSD的训练流程，来使网络得到更好的训练。先Dense训练，获得一个网络权重；然后spars将网络剪枝，然后继续dense训练。从而获得更好的性能。

1.2 提升模型准确率

实验显示DSD在CNN，RNN，LSTM等图像分类、图像识别，语音识别等模型上都取得了很好的效果。

将GoogleNet的Top1 accuracy提升了 1.1%
VGG-16提升了4.3%
ResNet-18提升了1.2%
ResNet-50提升了1.1%

1.3. 易于实施

DSD易于实施，只在S阶段引入一个超参数，其他阶段也更易实现。

二、方法

2.1 区别

与dropout的区别

虽然都是在训练过程中有prune（剪枝）操作，但是DSD是有一定依据来选择去掉哪些connection，而dropout是随机去掉。

与模型压缩的区别

DSD的目的是提升准确率，不能带来模型的精简。

2.2 算法流程

D：将网络正常训练，获得相应的权重

S：将网络剪枝，将小于某值的权重去掉，然后继续训练。

D：将剪枝的权重恢复为0，重新训练网络。

2.3 相应权重的变化

（a）上图为权重的直方图。我们看到第一次Dense训练之后，权重分布都有，且在各处分布

（b）将绝对值小于某值的权重删除掉，我们看到某绝对值一下的权重都没有了

（c）进行sparse训练，我们看到边缘变得平滑。

（d）恢复剪枝的权重，全部置为0。则0值有一个高峰。

（e）再次进行训练，权重各处都有分布。

2.4 具体流程及解释

Initial Dense Training

即普通神经网络的训练方法，但此步的目的是1.学出权重的值 2.学出哪些权重更重要（绝对值越大则权重越重要）。

Sparse Training

按比例将小于某绝对值权重值的值置为0。

进行剪枝的数学推导：

假定我们有一个loss，loss受到权重值的影响，是权重值的函数。

权重值变化会带来Loss值的变化：

所以权重值越小，则置为0带来的权重的变化越小，Loss值的变化也越小。

Final Dense Training

恢复被剪枝的权重置为0，重新训练。

三、实验

（略）

四、讨论与原理

DSD带来了准确率的提升，作者进行了下面这些讨论：

跳过了鞍点（Saddle Point）

鞍点：鞍点（Saddle point）在微分方程中，沿着某一方向是稳定的，另一条方向是不稳定的奇点，叫做鞍点。在矩阵中，一个数在所在行中是最大值，在所在列中是最小值，则被称为鞍点。在物理上要广泛一些，指在一个方向是极大值，另一个方向是极小值的点。

鞍点梯度接近于0，模型接近于收敛。但是剪枝的过程跳过了这些点。

更好的局部极小值（Better Minima）

低权重置为0就获得了更好的局部极小值。（对此作者没有具体解释）

正则化与稀疏训练

稀疏的正则化将模型拉到了更低的维度，因此可以对于噪声更加鲁棒。

鲁棒的再次初始化

普通的模型只初始化一次，但是DSD进行了两次（或更多）的权值初始化。这里作者给出了一个猜想，作者采用的是0值初始化的方法，其他的初始化方法值得尝试。

打破了对称性（Symmetry）

剪枝能破坏权值的对称性，所以获得更好的训练。（此处不明意义，作者未给出详尽解释，我对于symmetry的理解不够好。贴出原文）

Break Symmetry: The permutation symmetry of the hidden units makes the weights symmetrical,thus prone to co-adaptation in training. In DSD, pruning the weights breaks the symmetry of the hidden units associated with the weights, and the weights are asymmetrical in the final dense phase.

---

韩松EIE:Efficient Inference Engine on Compressed Deep Neural Network论文详解

https://blog.csdn.net/weixin_36474809/article/details/85326634

EIE为韩松博士在ISCA 2016上的论文。实现了压缩的稀疏神经网络的硬件加速。与其近似方法的ESE获得了FPGA2017的最佳论文。

通过剪枝和量化训练 [25] [26] 实现的深度压缩能够大幅降低模型大小和读取深度神经网络参数的内存带宽。但是，在硬件中利用压缩的 DNN 模型是一项具有挑战性的任务。尽管压缩减少了运算的总数，但是它引起的计算不规则性对高效加速带来阻碍。例如，剪枝导致的权重稀疏使并行变的困难，也使优秀的密集型线性代数库无法正常实现。此外，稀疏性激活值依赖于上一层的计算输出，这只有在算法实施时才能知道。为了解决这些问题，实现在稀疏的压缩 DNN 模型上高效地运行，我们开发了一种专门的硬件加速器 EIE，它通过共享权重执行自定义的稀疏矩阵乘法，从而减少内存占用，并在执行推断时实现大幅加速和能耗节约。
————————————————
本文为CSDN博主「机器之心V」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/Uwr44UOuQcNsUQb60zk2/article/details/78334036

一、背景与介绍

1.1 Motivation

最新的DNN模型都是运算密集型和存储密集型，难以硬件部署。

1.2 前期工作

Deep compression 通过剪枝，量化，权值共享等方法极大的压缩了模型。Deep compression解析见下链接

https://blog.csdn.net/weixin_36474809/article/details/80643784

1.3 贡献点

提出了EIE （Efficient Inference Engine）的方法，将压缩模型应用与硬件。
对于压缩网络来说，EIE可以带来120 GOPS/s 的处理效率，相当于同等未压缩的网络 3TGOP/s的处理效率。(AlexNet需要1.4GOPS，ResNet-152需要22.6GOPS)
比CPU和GPU带来24000x和3400x的功率提升。
比CPU，GPU和Mobile GPU速度快189x， 13x，307x

二、方法

2.1 公式描述

神经网络的基本运算

对于神经网络中的一个Fc层，相应的运算公式是下面的：

其中，a为输入，v为偏置，W为权重，f为非线性的映射。b为输出。此公式即神经网络中的最基本操作。

对于神经元的运算

针对每一个具体的神经元，上面的公式可以简化为下面这样：

输入a与权重矩阵W相乘，然后进行激活，输出为b

Deep compression后的公式

Deep compression将相应的权重矩阵压缩为一个稀疏的矩阵，将权值矩阵Wij压缩为一个稀疏的4比特的Index Iij，然后共享权值存入一个表S之中，表S有16种可能的权值。所以相应的公式可以写为：

即位置信息为i，j，非零值可以通过Iij找到表S中的位置恢复出相应的权值。

查表与值

权值的表示过程经过了压缩。即CSC与CRC的方法找到相应的权值，即

具体可以参考Deep compression或者网上有详细的讲解。

https://blog.csdn.net/weixin_36474809/article/details/80643784

例如上面的稀疏矩阵A。我们将每一个非零值存下来在AA中。

JA表示换行时候的第一个元素在AA中的位置。例如A中第二列第一个元素在A中为第四个，第3行元素在A中为第6个。

IC为对应AA每一个元素的列。这样通过这样一个矩阵可以很快的恢复AA表中的行和列。

2.2 矩阵表示（重要）

这是我加入的对上图2图3的理解。

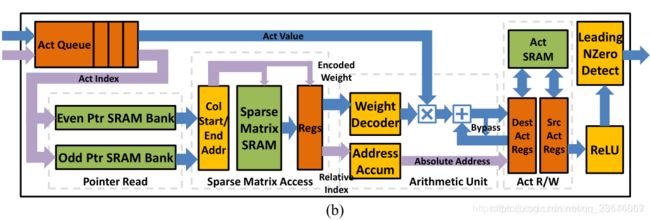
三、硬件实现

PE之间用H-tree结构，可以保证PE数量增加时布线长度以log函数增长（增长最缓慢的形式）

四、实验情况

实现平台

作者运用Verilog将EIE实现为RTL，synthesized EIE using the Synopsys Design Compiler (DC) under the TSMC 45nm GP standard VT library with worst case PVT corner. 运用台积电45nm和最差的PVT corner。作者用较差的平台来体现压缩及设计带来的数据提升。

We placed and routed the PE using the Synopsys IC compiler (ICC).We annotated the toggle rate from the RTL simulation to the gate-level netlist, which was dumped to switching activity interchange format (SAIF), and estimated the power using Prime-Time PX.

速度与功耗

运算平台：不同颜色是不同架构的运算平台，如CPU为Intel core i7 5930k，GPU为NVIDIA GeForce GTX Titan X，mobilt GPU为NVIDIA的cuBLAS GEMV。我们看到EIE起到了最快的效果。

运行的神经网络：如下：

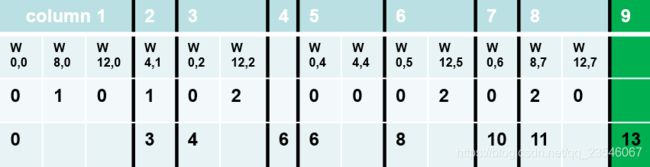
运行时间见下表

负载平衡中FIFO队列的长度

负载平衡见3.2 ，FIFO为先进先出队列，用于存储CCU发来的数据给PE进行处理。FIFO越长越利于负载平衡

因为每个PE分得的是否为稀疏的数量为独立同分布的，所以FIFO越长，其总和的方差越小。所以增大FIFO会有利于PE之间的负载平衡。

SRAM的位宽度

SRAM的位宽度接口，位宽越宽则获取数据越快，读取数据次数越少（下图绿线），但是会增大功耗（蓝色条）。如下图：

总体的能量消耗需要两者相乘，如下：

运算精度

作者运用的是16bit定点运算。会比32bit浮点减少6.2x的功率消耗，但是会降低精度。

并行PE数对速度的提升

与同类工作的对比

内容较多，感兴趣自行查看原文。