大白话解析Apriori算法python实现(含源代码详解)
大白话解析Apriori算法python实现(含源代码详解)
- 一、专业名词解释
- 二、算法思路
- 三、python代码实现
- 四、Aprioir的优点、缺点及改进方法
本文为博主原创文章,转载请注明出处,并附上原文链接。
原文链接: https://blog.csdn.net/qq_39872846/article/details/105291265
前言:Apriori算法是关联规则挖掘算法,也是最经典的算法。(它的进阶算法有FpGrowth算法,通过构造一个树结构来压缩数据记录,使得挖掘频繁项集只需要扫描两次数据记录,且该算法不需要生成候选集合,具体算法实现及python实现,可以移步到我另一篇博客–>简单详细叙述FpGrowth算法思想(附python源码实现))
Apriori算法是为了发现事物之间的联系的算法,比如我们熟知的啤酒与尿布故事,某超市在对顾客购物习惯分析时,发现,男性顾客在购买婴儿尿片时,常常会顺便搭配几瓶啤酒来犒劳自己,于是尝试推出了将啤酒和尿布摆在一起的促销手段,最后使得啤酒与尿布销量双双提升。
我们的Aprioir算法就是为了发现这样的关联而产生的,在文章中我会尽量用通俗的语言,讲解这个算法的思路,由于笔者水平有限,文章可能太过冗余,敬请谅解。
一、专业名词解释
假如现在有一组购物数据,共4条记录,每条记录都是一个顾客在超市购买商品产生的数据(我们只关心顾客买的种类,不关心它买了这类商品的数量,因为我们要找到是商品种类之间的关联,不是数量的关联)。
现在假设有5种商品,A B C D E,为了程序实现,把它换成数字表示更好一点A–>1, B–>2, C–>3, D–>4, E–>5 。
下面是这4条数据,把种类ABCDE换成数字 1 2 3 4 5。
[A C D] --> 1 3 4
[B C E] --> 2 3 5
[A B C E] --> 1 2 3 5
[B E] --> 2 5
1、什么是关联规则
现在有一个人,超市老板小红,她拿到了这组数据,想找出哪些商品是有关联的,关联是什么意思呢?举个例子,比如,你想买个泡面,你一桶面不够吃,两桶吃不了,你是不是就想,要不我在顺便买个香肠?还不够!在加个蛋呢?实在不行,再加个鸡腿!
好了,现在你就明白了,泡面、香肠、鸡蛋、鸡腿,这4个商品可能就是关联的,如果超市把这几个放在一起,你在买泡面的时候,是不是一不小心就多消费了(万恶的资本家啊),你就会不由感受到,现在连泡面都吃不起了。
2、支持度
继续思考怎样找出这些关联商品,小红现在有4条数据记录(实际的超市,每天产生的数据可能上千,我们这里就简化一点,方便理解),小红很聪明,她认为,如果某一种商品组合(这个组合,可以是1个,或者2个,甚至3个以上的不同种类商品的组合),在整条数据库中出现的次数太少,那我就认为他们没有关联, 这个道理很显然,比如,商品组合AB,假如A是白酒,B是头孢(不要问我为什么超市会卖药,反正它现在就得卖→_→),这两个一起吃可能会中毒,那么你在买酒的时候肯定不会刻意去买头孢吧(不要说是给女朋友买的 ̄へ ̄,来自单身狗的怨念),换句话说,如果你买了A,大概率不会买B,甚至会刻意不去买B,那么AB同时出现在一条购物记录的次数必然不会太多,因此可以认为两者没有关联。
那小红又在想,这个商品组合出现的次数小于多少,我才认为它是无关联的呢?
这个次数可以随意规定,我们称为支持度。但你试想一下,如果这个数定的太小,连 酒 和 头孢 您都认为有关联,然后 你把这两个摆在一起卖,显然不合适,算法意义也不大。如果定的太高,很多商品本来有关联,结果你定的太高,这些商品组合出现次数都不能满足这个数,那么这些商品组合你也就找不出来,算法也就失去了意义。所以这个值一定要取的合适才好。
这个取值就称为 最小支持度。
对应于我们文中的例子,
A在四条记录中出现了2次,它的最小支持度min_support(A)=2,这是以它出现的次数作为最小支持度。
还可以用A出现的概率来表示,就是 A出现的次数 ÷ 总记录次数
A出现的次数是2,我们总共有4条数据,最小支持度也可以表示为:
min_support(A)=2/4=0.5
在看一下BE的最小支持度:
BE同时出现的次数为3次,总记录数依旧是4条,
那 min_support(BE)=3 或 min_support(BE)=3/4
(在代码中用那种形式表示都可以,表示的意义是一样的)
3、置信度
小红又要开始想了(前面提到过她很聪明,手动狗头),只用次数大小来确定是否关联,是不是太草率了,假如你去买泡面,这个月钱快见底了(肯定啊,谁有钱会吃泡面),你打算买3或4包,到了地方,里面有很多口味的,比如麻辣,原味,三鲜,酸菜,但你就喜欢麻辣的,本来是想全买麻辣口味的,可惜的是每种口味都只剩2包了,无奈之下,你买了2包麻辣,还有1包酸菜的,走之前还拿了个蛋,,,这个时候你的这条购物信息是 {麻辣, 酸菜, 蛋},前面说了,我们不关心数量,只关心种类。
这个时候,虽然购物记录里面有 麻辣,和酸菜两种物品,但你要知道,你刚开始是想全买麻辣的,是因为麻辣的没了,才买了酸菜。虽然{麻辣,酸菜}同时出现了,且在计算支持度时,还提供了次数,可能会误认为麻辣和酸菜是 相关的,但其实你知道你是无奈才选的酸菜泡面,麻辣和酸菜并不是相关的,甚至顾客在买麻辣口味的时候,刻意不会去购买酸菜口味的泡面,它们是反相关的。
如果能计算出,顾客在买了麻辣的情况下,同时买了酸菜的概率多好啊,如果这个概率大,就表明顾客买了麻辣的,还要买酸菜的情况不是偶然,顾客就是同时喜欢吃这两种口味,每次买泡面,总是同时买这两种口味,两种口味是关联的。如果概率小,就表明顾客只喜欢其中一种口味,买酸菜是因为无奈之举,超市没货了。
现在就清楚了,我们算一下这个概率,很明显是条件概率的计算,用AB表示这两种商品,则 AB同时出现的次数 ÷ A单独出现的次数,就是顾客在买A的前提下,又买了B的概率,这个概率又称为 置信度,这个式子的意思表示,对于顾客 <买了A,同时又买了B的行为> 有多少自信,有多少把握,认为这个商品组合是有关联的。
和支持度类似,我们也得自己确定一个数,称为最小置信度,大于这个数就认为这个商品组合有关联。
- 下面对于文章给出的数据计算一下置信度:以BC为例
如:BC同时出现的次数为2,B单独出现的次数为3,
则置信度confidence(C–>B)=2/3,称为顾客 <买了C的情况下,又买了B的这个行为> BC具有关联性质的把握为2/3,换句话说,就是顾客买了C后,有 2/3 的概率去买B。
再算一下 顾客买了B的情况下,又买了C的置信度是多少,
BC同时出现的次数依旧为2,C单独出现的次数为3
confidence(B–>C)=2/3,称为顾客 <买了B的情况下,又买了C的这个行为> 的可信度2/3,换句话说,就是顾客买了C后,有 2/3的概率去买B。
(当然,我们使用的数据太少,有些数据计算出来是100%,这完全是巧合,如果数据足够大,这个概率就就不会这样夸张了)
!!!要注意 :只有当这个商品组合的支持度大于它的最小支持度并且置信度大于最小置信度,我们才认为这个商品组合是强关联的,我们称这个商品组合为频繁项集。(为了简化代码,我仅仅只用了支持度,如果某种商品组合的支持度 大于 最小支持度,就认为是频繁项集。 并没有用到最小置信度,,如果读者有能力,可以自己做出改进,只需要在求频繁项集的时候,在保持这种商品组合的支持度大于最小支持度的情况下,同时保证该商品组合的置信度 大于 最小置信度 即可。)
(从公式可以看出,AB同时出现的次数其实就是AB的支持度,A单独出现的次数就是A的支持度,支持度可以用次数表示,也可以用频率表示,如用概率表示,则置信度confidence公式如下)
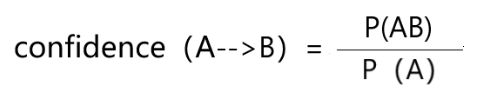
4、提升度
(也是一个度量某种商品组合是否为频繁项集的量(和支持度,置信度类似),大家可以了解一下,这个量我在代码中也没有体现,就是为了简化代码)
这时候小红还觉得不放心,她又思索了一下,发现这样一种情况:假如原来一个商品X,在总记录中出现的概率是80%(也就是支持度),但是XY两种商品同时出现的概率是50%,是不是在一定程度上,Y商品的出现反而降低了原来的商品X的销售额?
我们首先来看一个式子,

分析这个式子,对于P(AB),
- 如果A,B两个相互独立,即A发生不会影响到B,那么P(AB)=P(A)P(B),显然,最后这个式子结果为1
- 如果A,B不独立,即A发生会影响到B的发生,但是要注意,我们不能确定这个影响是什么类型,即A发生可能导致B发生的概率增加,也有可能A发生会导致B发生的概率减小。
上面这个式子就是提升度计算公式,即提升度 Lift(A–>B)为:
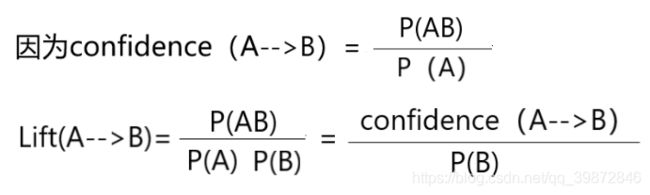
例子,我们来看一下文章给出的数据,比如BC:
BC同时出现的次数为2,支持度support(B–>C)=2/4
C单独出现的次数为3,支持度support(C)=3/4
B单独出现的次数为3,支持度support(B)=3/4
由以上数据可计算出B–>C的置信度,
confidence(B–>C)= support(B–>C) ÷ support(B) = 2/3
则提升度:
Lift(B–>C)=confidence(B–>C) ÷ support( C) = 8/9
因为提升度小于1,所以可以确定,购买B时,会降低对C的购买,如果计算出来提升度大于1,说明购买B时,会促进C的购买。
二、算法思路
先来看两个定律:
Apriori定律1 :如果某商品组合小于最小支持度,则就将它舍去,它的超集必然不是频繁项集。
Apriori定律2 :如果一个集合是频繁项集,即这个商品组合支持度大于最小支持度,则它的所有子集都是频繁项集
- 俩个定律都很容易理解,举个例子,
-对于定律1,假如有AB这个商品组合,它的出现的次数小于2,那么你还会指望ABC同时出现的次数大于2吗?
-对于定律2,假如ABC同时出现的次数比2大,那么不管是AB、AC、BC它门同时出现的次数至少不会比2小把。
如何实现算法?有两步
1、找出所有频繁项集。
就是该商品组合的支持度 大于 最小支持度
2、由频繁项集确定下一组候选集。(在下面的讲解中有具体说明)
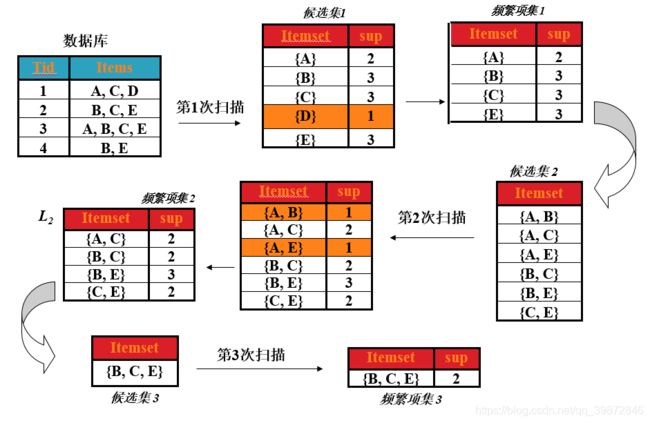
(1)第一次扫描
首先,求第一次扫描数据库后的候选集。
从图中可以看出,第一次扫描后,可以求出单个商品的支持度(图中支持度用出现次数表示),这个表称为第一次候选集,即下图所示:
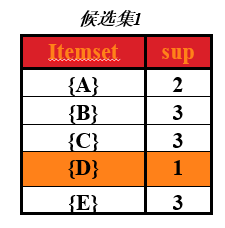
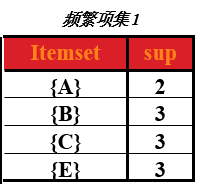
在第一次候选集基础上,求出第一次频繁项集,频繁项就是该商品的支持度 大于 最小支持度,支持度选择时随意的,在这里取最小支持度为 min_support=2
那么第一次频繁项集就是第一次候选集中,支持度大于或大于2的所有商品集合。即下表,(把 D 商品从表中去除了,因为它的支持度小于2)
(2)第二次扫描
先求出第二次的候选集。
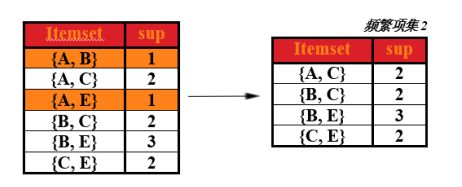
即在第一次频繁项集的基础上,找出第二次候选集,对商品进行组合,形成一个2元组,4种商品,不同组合有C42种,即 4x3=12 种,形成的表称为第二次候选集表。如下图

在求第二次频繁项集
对于上表,求出这两种商品同时出现在总记录中的次数(即求支持度),然后去掉支持度小于2的商品组合,形成的表即为第二次频繁项集。如下表
(3)第三次扫描
先求出第三次的候选集。
即在第二次频繁项集的基础上,找出第三次候选集。
就是将原来的2元组,拓展为3元组,怎么拓展呢?
设K为第K次扫描,要求第K个候选集,找出上一次扫描的频繁项集,然后观察里面的记录,对于里面的每个记录,前(K-2)个前缀相同的,归为一类,在同一类别中进行合并。
比如 这第三次扫描,要求出它的候选集,先找出上次扫描形成的第二次频繁项集表,里面有4条记录,分别为,AC,BC,BE,CE,这些记录中,前(K-2)个前缀,就是前(3-2)个前缀,也就是第一个前缀相同的归为一类,接着在属于同一类的记录中,进行合并,比如BC,BE,它门的第一个前缀都是B,那么在这一类中,把它门合并起来就形成了BCE。还剩下AC、CE,它门第一个前缀不相同,也没有其他元素和它门相同,那么就不用去管了。如果你非要合并,把AC、CE合并为ACE,我们看一下ACE的子集,它的子集是{AC、CE、AE},可以看出AC、CE确实是频繁项集,但是AE呢,你在求第二次的候选集时,因为AE的支持度小于2,你把它去除了,那么ACE也必然不是频繁项集。(Apriori定律1 :如果某商品组合小于最小支持度,则就将它舍去,它的超集必然不是频繁项集。)
-----------在这里要说明一下减枝的概念
比如刚才新形成的BCE这个组合,它的子集是{BC、CE、BE},显然BC和CE本来就是一个频繁项集,但是CE呢,我们必须对比上一次频繁项集中的元素,也就是第2次频繁项集的元素,如果CE不是第二次频繁项集的元素,那么就把新形成的 BC E 这个元素给 “减去”,也就是减枝,这一点我在代码中有体现,具体请看后面的代码。
(4)第四次扫描和前两次原理,一样,留给读者做练习。
最后值得一提的是,当最后生成的候选集表中,只有0个或1个的话,循环就结束了。
三、python代码实现
运行环境: python3.6 PyCharm编译器
算法如下:
'''
#请从最后的main方法开始看起
Apriori算法,频繁项集算法
A 1, B 2, C 3, D 4, E 5
1 [A C D] 1 3 4
2 [B C E] 2 3 5
3 [A B C E] 1 2 3 5
4 [B E] 2 5
min_support = 2 或 = 2/4
'''
def item(dataset): #求第一次扫描数据库后的 候选集,(它没法加入循环)
c1 = [] #存放候选集元素
for x in dataset: #就是求这个数据库中出现了几个元素,然后返回
for y in x:
if [y] not in c1:
c1.append( [y] )
c1.sort()
#print(c1)
return c1
def get_frequent_item(dataset, c, min_support):
cut_branch = {} #用来存放所有项集的支持度的字典
for x in c:
for y in dataset:
if set(x).issubset(set(y)): #如果 x 不在 y中,就把对应元素后面加 1
cut_branch[tuple(x)] = cut_branch.get(tuple(x), 0) + 1 #cut_branch[y] = new_cand.get(y, 0)表示如果字典里面没有想要的关键词,就返回0
#print(cut_branch)
Fk = [] #支持度大于最小支持度的项集, 即频繁项集
sup_dataK = {} #用来存放所有 频繁 项集的支持度的字典
for i in cut_branch:
if cut_branch[i] >= min_support: #Apriori定律1 小于支持度,则就将它舍去,它的超集必然不是频繁项集
Fk.append( list(i))
sup_dataK[i] = cut_branch[i]
#print(Fk)
return Fk, sup_dataK
def get_candidate(Fk, K): #求第k次候选集
ck = [] #存放产生候选集
for i in range(len(Fk)):
for j in range(i+1, len(Fk)):
L1 = list(Fk[i])[:K-2]
L2 = list(Fk[j])[:K-2]
L1.sort()
L2.sort() #先排序,在进行组合
if L1 == L2:
if K > 2: #第二次求候选集,不需要进行减枝,因为第一次候选集都是单元素,且已经减枝了,组合为双元素肯定不会出现不满足支持度的元素
new = list(set(Fk[i]) ^ set(Fk[j]) ) #集合运算 对称差集 ^ (含义,集合的元素在t或s中,但不会同时出现在二者中)
#new表示,这两个记录中,不同的元素集合
# 为什么要用new? 比如 1,2 1,3 两个合并成 1,2,3 我们知道1,2 和 1,3 一定是频繁项集,但 2,3呢,我们要判断2,3是否为频繁项集
#Apriori定律1 如果一个集合不是频繁项集,则它的所有超集都不是频繁项集
else:
new = set()
for x in Fk:
if set(new).issubset(set(x)) and list(set(Fk[i]) | set(Fk[j])) not in ck: #减枝 new是 x 的子集,并且 还没有加入 ck 中
ck.append( list(set(Fk[i]) | set(Fk[j])) )
#print(ck)
return ck
def Apriori(dataset, min_support = 2):
c1 = item (dataset) #返回一个二维列表,里面的每一个一维列表,都是第一次候选集的元素
f1, sup_1 = get_frequent_item(dataset, c1, min_support) #求第一次候选集
F = [f1] #将第一次候选集产生的频繁项集放入 F ,以后每次扫描产生的所有频繁项集都放入里面
sup_data = sup_1 #一个字典,里面存放所有产生的候选集,及其支持度
K = 2 #从第二个开始循环求解,先求候选集,在求频繁项集
while (len(F[K-2]) > 1): #k-2是因为F是从0开始数的 #前一个的频繁项集个数在2个或2个以上,才继续循环,否则退出
ck = get_candidate(F[K-2], K) #求第k次候选集
fk, sup_k = get_frequent_item(dataset, ck, min_support) #求第k次频繁项集
F.append(fk) #把新产生的候选集假如F
sup_data.update(sup_k) #字典更新,加入新得出的数据
K+=1
return F, sup_data #返回所有频繁项集, 以及存放频繁项集支持度的字典
if __name__ == '__main__':
dataset = [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]] #装入数据 二维列表
F, sup_data = Apriori(dataset, min_support = 2) #最小支持度设置为2
print("具有关联的商品是{}".format(F)) #带变量的字符串输出,必须为字典符号表示
print('------------------')
print("对应的支持度为{}".format(sup_data))
四、Aprioir的优点、缺点及改进方法
Aprori算法利可以很好的找出关联关系,但是每一次求候选集都需要扫描一次所有数据记录,那么在面临千万级别的数据记录就显得有点无力了。
因此FpGrowth算法出现了,它是通过构造一个树结构来压缩数据记录,使得挖掘频繁项集只需要扫描两次数据记录,且该算法不需要生成候选集合,所以效率会比较高。以后有时间在记录一下这个算法的思想。(FpGrowth算法已经写出来了,大家可以去看看哦–>简单详细叙述FpGrowth算法思想(附python源码实现))
本人学识尚浅,文章中难免有错误存在,还请大家指正,不胜感激!