论文研读 —— 矩阵乘积算符对深层神经网络的优化
前两天我主要学习了卷积神经网络的一些相关理论，并写成了一篇博客，这一期 ，基于前面学习过张量中矩阵乘积态的相关基础理论和深度学习中的卷积神经网络，我们下面将学习论文中 是如何将这二者完美的结合在一起！
矩阵乘积算符对深层神经网络的优化
- 一.深度学习简介
- 二 . 矩阵乘积算符回顾
- 三 . 全连接层与MPO的结合
一.深度学习简介
作为机器学习最重要的一个分支，深度学习近年来发展迅猛，在国内外都引起了广泛的关注。然而深度学习的火热也不是一时兴起的，而是经历了一段漫长的发展史。接下来我们通过一张图片就可以大概的了解一下它的发展历程：
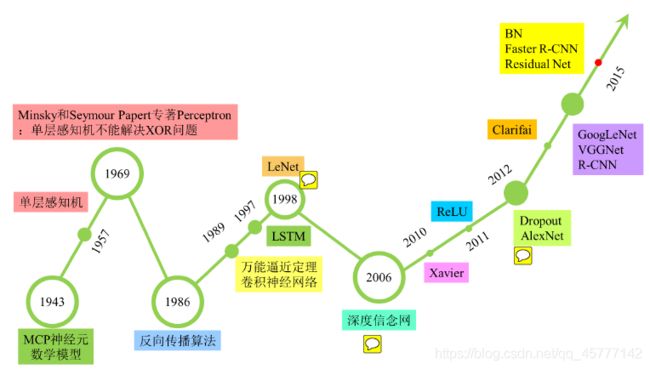
作为机器学习发展到一定阶段的产物，近年来深度学习技术之所以能引起社会各界广泛的关注，是因为不光在学术界，同时也在工业界取得了重大突破和广泛的应用。其中应用最广的几个研究领域分别是自然语言处理、语音识别和图像处理。
而我们这里需要深度理解学习的就是图像处理部分：
事实上，图像领域目前算是深度学习应用最为成熟的领域。也正是由于深度学习算法在ImageNet图像识别大赛中远超其它机器学习算法、以巨大优势夺魁才推动了深度学习发展的第三次浪潮。目前，通过卷积神经网络（CNN）构建的图像处理系统能够有效的减小过拟合、对大像素数图像内容能很好的识别，在融合GPU加速技术后，使得神经网络在实际中能够更好的拟合训练数据，更快更准确的识别大部分的图片。总而言之，深度学习模型可谓是和图像处理技术的完美结合，不仅能够提高图像识别的准确率，同时还可以在一定程度上提高运行效率，减少了一定的人力成本！
虽然对于一些特殊图像的处理我们的CNN 略有不同，但是CNN的 层级结构却总是确定的：即卷积计算层，全连接层，池化层和 非线性的元素激活步骤！
结合我们之前学习的 minist 手写数据集，这里的全连接层就是用过一定的函数将输入数据信号最终返回对应的预测标签值。那么全连接层的操作可以用如下
函数表示：
y = W T x + b \mathbf{y}=W^{T} \mathbf{x}+\mathbf{b} y=WTx+b
在上次的 论文研读中，我们也学过这个函数，这里的 x 与 y 显然就是来自上层的输入和该层数据处理后的输出，通常是凭借向量或者矩阵的形式！W 就是 权重系数，它所代表的便是 输入神经元和输出神经元之间的关联强度，因为不同的数据特征矢量我们给予的 权重也是不同的！b 就是与y 同维度的一个偏置矢量！
根据我们前面所学的知识：一维哈密顿量的基态可以用矩阵乘积态来表示，多自旋量子态的系数算符可以用矩阵乘积态表示为矩阵乘积算符(MPO) , 至此 ，就将指数爆炸增长的问题转移为参数成线性增加的多项式增加模型！所以 ，如果我们能用这样的思想来代替深度学习中全连接层中的 大量参数，那么我们的图像数据问题 相关的计算难度会瞬间降低！
二 . 矩阵乘积算符回顾
我们之前的几期博客都详细的介绍了什么是矩阵乘积算符和相关的重要知识点，并且是结合多自旋量子态的算符方法，这里我们还需要做一个简单的回顾，温故而知新嘛！
这里我们就不再介绍张量的新表示法和相关的内容了，直接看一下对于多体量子态，如何用MPS 表示：一个量子态可以用一个完备基矢表示的波函数表示，例如对于N 体波函数 的 ∣ Ψ ⟩ |\Psi\rangle ∣Ψ⟩ 可以表示为：
∣ Ψ ⟩ = ∑ i 1 i 2 … i N C i 1 i 2 i 3 … i N ∣ i 1 i 2 … i N ⟩ |\Psi\rangle=\sum_{i_{1} i_{2} \ldots i_{N}} C_{i_{1} i_{2} i_{3} \ldots i_{N}}\left|i_{1} i_{2} \ldots i_{N}\right\rangle ∣Ψ⟩=i1i2…iN∑Ci1i2i3…iN∣i1i2…iN⟩
其实这里就是基矢的一个叠加，其对应的权重系数也就是张量元素 C i 1 i 2 i 3 … i N C_{i_{1} i_{2} i_{3} \ldots i_{N}} Ci1i2i3…iN , 那们，对于的物理算符系数就是：
O ^ = ∑ i 1 i 2 … i N , j 1 j 2 … j N O i 1 i 2 i 3 … i N j 1 j 2 … j N ∣ j 1 j 2 … j N ⟩ ⟨ i 1 i 2 … i N ∣ \hat{O}=\sum_{i_{1} i_{2} \ldots i_{N}, j_{1} j_{2} \ldots j_{N}} O_{i_{1} i_{2} i_{3} \ldots i_{N} j_{1} j_{2} \ldots j_{N}}\left|j_{1} j_{2} \ldots j_{N}\right\rangle\left\langle i_{1} i_{2} \ldots i_{N}\right| O^=i1i2…iN,j1j2…jN∑Oi1i2i3…iNj1j2…jN∣j1j2…jN⟩⟨i1i2…iN∣
这里我们在前面也做了非常详细的解释，可以假设每个粒子的局部自由度为 d d d , 对于所有 n n n , i n i_{n} in 从1 取到 d d d ,所以权重张量和算符系数张量的 分别具有 d N d^{N} dN 和 d 2 N d^{2N} d2N ，我们之前是以单自旋量子态和多自旋量子态为例，向大家详细解释过，传送门~~
我们传统的张量网络在可以转换为一维形式下的矩阵乘积态，对于前面的张量 C C C 和 O O O ,我们用公式表达：
C i 1 i 2 … i N = ∑ k 1 k 2 … k ( N − 1 ) A k 1 ( 1 ) [ i 1 ] A k 1 k 2 ( 2 ) [ i 2 ] … A k ( N − 1 ) ( N ) [ i N ] C_{i_{1} i_{2} \ldots i_{N}}=\sum_{k_{1} k_{2} \ldots k_{(N-1)}} A_{k_{1}}^{(1)}\left[i_{1}\right] A_{k_{1} k_{2}}^{(2)}\left[i_{2}\right] \ldots A_{k_{(N-1)}}^{(N)}\left[i_{N}\right] Ci1i2…iN=k1k2…k(N−1)∑Ak1(1)[i1]Ak1k2(2)[i2]…Ak(N−1)(N)[iN]
这里的 A ( i ) A^{(i)} A(i) 就是定义在 i i i 处理一个局域张量 ， k 1 , k 2 … k N k_{1},k_{2}\dots k_{N} k1,k2…kN 是我们引入的辅助指标，为的是把 原本的矩阵形式的局域张量链接在一起！并且每个局域张量都是直积的形式结合！对于物理算符 O O O 来说，它的公式表达为：
O i 1 ⋯ i N ； j 1 … j N = ∑ k 1 k 2 … k ( N − 1 ) B k 1 ( 1 ) [ i 1 j 1 ] B k 1 k 2 ( 2 ) [ i 2 j 2 ] … B k ( N − 1 ) ( N ) [ i N j N ] O_{i_{1} \cdots i_{N} ；j_{1} \ldots j_{N}}=\sum_{k_{1} k_{2} \ldots k_{(N-1)}}B_{k_{1}}^{(1)}\left[i_{1} j_{1}\right] B_{k_{1} k_{2}}^{(2)}\left[i_{2} j_{2}\right] \ldots B_{k_{(N-1)}}^{(N)}\left[i_{N} j_{N}\right] Oi1⋯iN；j1…jN=k1k2…k(N−1)∑Bk1(1)[i1j1]Bk1k2(2)[i2j2]…Bk(N−1)(N)[iNjN]
下面的图片分别对应这两个公式：
显然，（a） 是权重张量 C C C 和它的矩阵乘积态表示，（b） 就是物理算符系数 O O O 和它的矩阵乘积态表示！
说了这么多，引入这两个东西的主要目的就是减少参数，绕过指数墙这一问题！本来对与一个多粒子量子态的系数张量，它的维数有 2 N 2^{N} 2N,但是现在，我们回过头来看 ，参数只有 D 2 d ( N − 2 ) + 2 D d D^{2} d(N-2)+2 D d D2d(N−2)+2Dd ，这里的 D D D 就是我们增加的辅助指标的个数，也叫键维数。对于张量 O O O来说，参数减少为： D 2 d 2 ( N − 2 ) + 2 D d 2 D^{2} d^{2}(N-2)+2 D d^{2} D2d2(N−2)+2Dd2， N N N 越大，这里的优势就越明显！
三 . 全连接层与MPO的结合
我们再把目光转移到CNN上，对于一个完整的图像处理，我们一般把卷积核都会设置的非常小，因为在不知道具体图像包含的特征位置和数量的情况下，维度较小的卷积核能更好的为我们搜集图像信息，而卷积核过大可能会遗漏一小部分，又因为一般的图片维数非常高，在后面全连接层接受这些参数之后，代入相应的映射函数，又会增加参数的数量，比如：对于全连接层来说，输入 x 和输出 y 元素个数分别为 N N N 和 M M M ,那么权重参数矩阵 W W W 中元素就会是 N × M N\times M N×M 个，本身 N N N 和 M M M就已经很大了，这样对你的CPU来说就有点麻烦，所以我们需要探寻一种新方法！
根据前面所说，MPO的降维效果在全连接层的应用是否有效？
先将 W W W 中的大量参数分成 W i j = W i 1 i 2 … i n , j 1 j 2 … j n W_{i j}=W_{i_{1} i_{2} \ldots i_{n}, j_{1} j_{2} \ldots j_{n}} Wij=Wi1i2…in,j1j2…jn ，显然满足： ∏ i = 1 n I i = N , ∏ i = 1 n J i = M \prod_{i=1}^{n} I_{i}=N, \quad \prod_{i=1}^{n} J_{i}=M ∏i=1nIi=N,∏i=1nJi=M 。
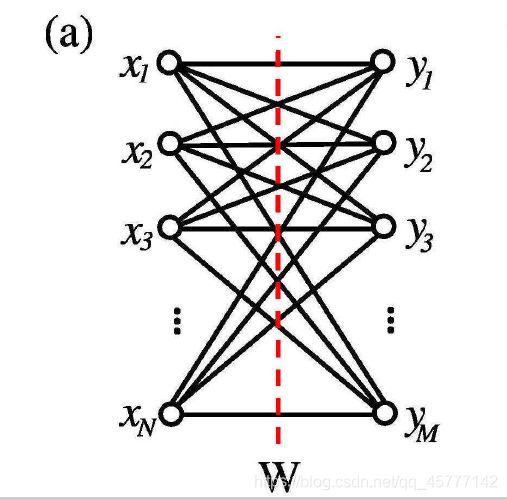这里我们就不再详细解释了，不过必须要知道的是，连接的实线就是权重系数，也就是组成 W W W 的元素！
直接将全连接层的权重系数 用MPO来表示为：
W i 1 i 2 … i n , j 1 j 2 … j n = ∑ k 1 k 2 … k ( n − 1 ) ω k 1 ( 1 ) [ i 1 j 1 ] ω k 1 k 2 ( 2 ) [ i 2 j 2 ] … ω k ( n − 1 ) ( n ) [ i n j n ] W_{i_{1} i_{2} \ldots i_{n}, j_{1} j_{2} \ldots j_{n}} =\sum_{k_{1} k_{2} \ldots k_{(n-1)}} \omega_{k_{1}}^{(1)}\left[i_{1} j_{1}\right] \omega_{k_{1} k_{2}}^{(2)}\left[i_{2} j_{2}\right] \ldots \omega_{k_{(n-1)}}^{(n)}\left[i_{n} j_{n}\right] Wi1i2…in,j1j2…jn=k1k2…k(n−1)∑ωk1(1)[i1j1]ωk1k2(2)[i2j2]…ωk(n−1)(n)[injn]
i i i 和 j j j正好和我们映射函数的输入和输出相对应，那 w ( i ) w^{(i)} w(i) 就是一个尺寸为 K i − 1 × K i K_{i-1} \times K_{i} Ki−1×Ki, ，当然开头结尾的局域张量还是三阶的， K K K依然是引入的虚拟辅助指标，图示表示为：
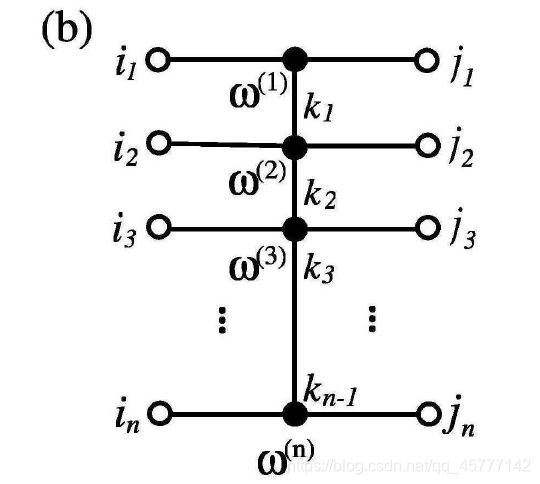这两个图片长得就非常的相似，空心圆圈代表的是指标 i m i_{m} im 和 i j i_{j} ij , w m [ i , j ] w^{m}[i,j] wm[i,j] 代表的是一个矩阵，（a）中 W W W 的左右两边代表的就是输入和输出！
这样的话，我们理论上是可以将维度大幅度降低，从而实计算效率的提升！