在MATLAB中利用符号函数功能,通过手动输入DH参数符号矩阵 or Excel文件导入DH参数表从而获得DH符号矩阵的公式
在MATLAB中利用符号函数功能,通过手动输入DH参数符号矩阵 or Excel文件导入DH参数表从而获得DH符号矩阵公式
- 1.前言
- 2.废话不多说,上代码演示效果
- 1. **函数使用方法一:==通过excel直接导入DH参数获得DH矩阵==**
- 2. **函数使用方法二:==将DH参数数据通过手动建立一个符号矩阵输入==**
- 注:本次利用到了matlab符号函数计算工具,具体的相关知识参考:
1.前言
由于自己的专业方向,现在正在开始学习机器人相关知识。在机器人领域中(特别是机械臂之类的工业机器人),如果需要对机器人进行运动学分析,我们常常需要用到D-H矩阵(即Denavit-Hartenberg矩阵)。
然而求过DH矩阵的小伙伴都知道,我们目前基本都是通过对应的DH参数表以及DH矩阵计算公式手动计算出各个DH转换矩阵。特别是在获得DH矩阵之后一般还需进行多个DH转换矩阵的相乘等操作,从而获得我们所需的变换关系。如果我们自己手动去计算这些矩阵,实在是恶心…
考虑到人工手动计算DH矩阵的麻烦,我便想“能不能利用工具,只要我输入DH参数就能自动算出对应的DH矩阵?”
今天,我在这里将要分享给大家的是一个自己写的 matlab 函数,这个函数便是用来求DH矩阵的。函数部分介绍如下:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 符号矩阵计算 DH 转换矩阵公式
% 1、函数功能:[Dof,A] = m_SigalMesu(DH_table_or_excelname,sheetname,range)
% 利用符号矩阵 or excel文件导入 D-H 参数表,自动获得转换矩阵
% DH_table_or_excelname —— DH参数符号矩阵 or 具有DH参数便表的excel文件名
% sheetname —— 只有在excel导入时候才有作用,它表示导入数据在excel文件的sheetname sheet中
% range —— 只有在excel导入时候才有作用,它表示DH参数表范围
% Dof —— 转换矩阵个数
% A —— 转换矩阵,三维数据。A(:,:,i)为求得的第i个DH矩阵
%
% 2、D-H参数输入格式:
% [连杆1长度a1 连杆1扭角aerf1 关节1偏移量d1 关节1角度theta1;
% 连杆2长度a2 连杆2扭角aerf2 关节2偏移量d2 关节2角度theta2;
% .... ]
% 符号矩阵直接创建方法:
% 1)M = sym('[a,2*b;3*a,0]');
% 2) M = str2sym('[a,2*b;3*a,0]');
% 注:sym函数可能不再适用
%
% 3、从excel导入输入格式:
% [Dof,A] = m_SigalMesu('excelname','sheetname','range')
% 如:[Dof,A] = m_SigalMesu('dh_test.xlsx','sheet1','B2:E8')
%
% 注:该函数如果输入一个参数,则表示输入为DH参数符号矩阵;
% 如果需要从excel导入,则需要根据自己建立的参数表输入:
% excel文件名、sheet名、甚至对应DH参数范围
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [Dof,A] = m_SigalMesu(DH_table_or_excelname,sheetname,range);
并且这样求得的矩阵还有个好处:利用matlab的符号运算功能,将获得的DH矩阵,能够直接通过matlab用于计算我们所需的变换矩阵!!!——从而不再需要我们自己手动计算 ~~~
由于创作不易,具体函数代码,大家如果需要,则到我主页下载;或留言邮箱~~~
下载网址:https://download.csdn.net/download/binheon/11180873
2.废话不多说,上代码演示效果
1. 函数使用方法一:通过excel直接导入DH参数获得DH矩阵
1)、建立一个excel文件,并将自己的DH参数按照固定格式(由于我在建这个函数时将格式给固定了,因此使用这函数时输入格式要按照固定格式来)输入到excel表中。如下例子:
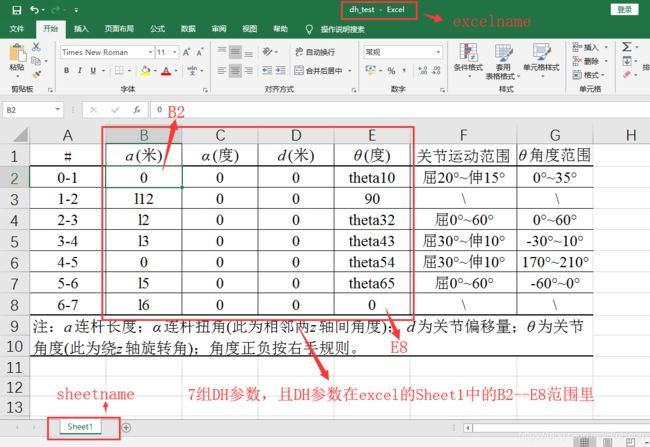
2)、直接调用函数,输入excel名、sheet名、表格范围
%%%% 从excel文件中导入数据,并求得DH矩阵
>>[Dof,A] = m_SigalMesu('dh_test.xlsx','sheet1','B2:E8') % 输入参数为:excel文件名、文件中对应的sheet名、表范围
Dof =
7 % DH矩阵个数
A(:,:,1) =
[ cos(theta10), -sin(theta10), 0, 0]
[ sin(theta10), cos(theta10), 0, 0]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1] % 第1个DH矩阵函数
A(:,:,2) =
[ cos(90), -sin(90), 0, l12*cos(90)]
[ sin(90), cos(90), 0, l12*sin(90)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1] % 第2个DH矩阵函数
A(:,:,3) =
[ cos(theta32), -sin(theta32), 0, l2*cos(theta32)]
[ sin(theta32), cos(theta32), 0, l2*sin(theta32)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1] % 第3个DH矩阵函数
A(:,:,4) =
[ cos(theta43), -sin(theta43), 0, l3*cos(theta43)]
[ sin(theta43), cos(theta43), 0, l3*sin(theta43)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,5) =
[ cos(theta54), -sin(theta54), 0, 0]
[ sin(theta54), cos(theta54), 0, 0]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,6) =
[ cos(theta65), -sin(theta65), 0, l5*cos(theta65)]
[ sin(theta65), cos(theta65), 0, l5*sin(theta65)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,7) =
[ 1, 0, 0, l6]
[ 0, 1, 0, 0]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
>>
Dof——为DH参数组的数目,也是DH矩阵的个数;
A——便是返回的DH参数的集合;它是一个三维数据,因而A(:,:,i)就是第i个DH矩阵。
这样一个求DH矩阵的函数,只要输入了 DH参数 就能简简单单的获得对应的 DH矩阵。
3)、如果还需要求转换关系,如求0到7之间的转换关系矩阵(即求0到7的7个DH矩阵的乘积),直接将得到的DH矩阵相乘:
A(:,:,1)*A(:,:,2)*A(:,:,3)*A(:,:,4)*A(:,:,5)*A(:,:,6)*A(:,:,7)
%%%% 直接相乘:T = A(:,:,1)*A(:,:,2)*A(:,:,3)*A(:,:,4)*A(:,:,5)*A(:,:,6)*A(:,:,7)
%%%% 考虑到函数的复杂性,最好利用simplif()函数化简下:
>>T = simplify(A(:,:,1)*A(:,:,2)*A(:,:,3)*A(:,:,4)*A(:,:,5)*A(:,:,6)*A(:,:,7))
T =
[ cos(theta10 + theta32 + theta43 + theta54 + theta65 + 90), -sin(theta10 + theta32 + theta43 + theta54 + theta65 + 90), 0, l12*cos(theta10 + 90) + l2*cos(theta10 + theta32 + 90) + l5*cos(theta10 + theta32 + theta43 + theta54 + theta65 + 90) + l6*cos(theta10 + theta32 + theta43 + theta54 + theta65 + 90) + l3*cos(theta10 + theta32 + theta43 + 90)]
[ sin(theta10 + theta32 + theta43 + theta54 + theta65 + 90), cos(theta10 + theta32 + theta43 + theta54 + theta65 + 90), 0, l12*sin(theta10 + 90) + l2*sin(theta10 + theta32 + 90) + l5*sin(theta10 + theta32 + theta43 + theta54 + theta65 + 90) + l6*sin(theta10 + theta32 + theta43 + theta54 + theta65 + 90) + l3*sin(theta10 + theta32 + theta43 + 90)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
simplify()函数是用于符号函数的化简,具体有关符号函数化简,以及matlab的符号函数、符号矩阵的知识可查看下链接:
https://wenku.baidu.com/view/e488e5decc7931b764ce15c4.html
或
https://wenku.baidu.com/view/4a21893800f69e3143323968011ca300a6c3f621.html
2. 函数使用方法二:将DH参数数据通过手动建立一个符号矩阵输入
1)、通过手动方式输入DH参数,且输入格式必须按照函数注释的格式输入。
同样以下的excel中的DH参数为例:

那么函数的使用如下:
%%%% 1、首先建立一个DH参数符号矩阵DH_TABLE
syms l12 l2 l3 l5 l6 theta10 theta32 theta43 theta54 theta65 % 定义符号参数
DH_TABLE = [0 , 0, 0, theta10;
l12 , 0, 0, 90;
l2 , 0, 0, theta32;
l3 , 0, 0, theta43;
0 , 0, 0, theta54;
l5 , 0, 0, theta65;
l6 , 0, 0, 0 ] % 定义DH参数表
DH_TABLE =
[ 0, 0, 0, theta10]
[ l12, 0, 0, 90]
[ l2, 0, 0, theta32]
[ l3, 0, 0, theta43]
[ 0, 0, 0, theta54]
[ l5, 0, 0, theta65]
[ l6, 0, 0, 0]
%%%% 或者直接:DH_TABLE = str2sym('[0,0,0,theta10;l12,0,0,90;l2,0,0,theta32;l3,0,0,theta43;0,0,0,theta54;l5,0,0,theta65;l6,0,0,0]')
%%%% str2sym()函数直接能够生产符号矩阵,但是如果需要带具体数值到所得矩阵公式中计算的话,该定义符号矩阵的方式则不行
%%%% 2、直接调用求DH参数函数求得DH矩阵
>>[Dof,A] = m_SigalMesu(DH_TABLE)
Dof =
7
A(:,:,1) =
[ cos(theta10), -sin(theta10), 0, 0]
[ sin(theta10), cos(theta10), 0, 0]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,2) =
[ cos(90), -sin(90), 0, l12*cos(90)]
[ sin(90), cos(90), 0, l12*sin(90)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,3) =
[ cos(theta32), -sin(theta32), 0, l2*cos(theta32)]
[ sin(theta32), cos(theta32), 0, l2*sin(theta32)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,4) =
[ cos(theta43), -sin(theta43), 0, l3*cos(theta43)]
[ sin(theta43), cos(theta43), 0, l3*sin(theta43)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,5) =
[ cos(theta54), -sin(theta54), 0, 0]
[ sin(theta54), cos(theta54), 0, 0]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,6) =
[ cos(theta65), -sin(theta65), 0, l5*cos(theta65)]
[ sin(theta65), cos(theta65), 0, l5*sin(theta65)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,7) =
[ 1, 0, 0, l6]
[ 0, 1, 0, 0]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
这样便通过DH参数,首先建立一个符号矩阵,再传入求DH矩阵函数,便获得了对应的DH矩阵公式
2)、若需求转换矩阵,同样可直接选择对应的DH矩阵进行相乘等操作获得。如上面方法一中的3)部分代码。
3)、虽然从表面上看来,直接通过excel导入,更加方便。但是对于此求DH矩阵函数而言,由于对excel导入的数据并没进行过多的处理,因而从excel导入的DH参数不可出现特殊字符,也不可能出现 “+”、“-”、“*”、“/”(加、减、乘、除)符号。
!!!! 但是,如果通过建立符号矩阵的方式输入DH参数,参数中可以出现 “+”、“-”、“*”、“/”(加、减、乘、除)运算符号。如下:
%%%% 输入的DH参数具有“*”、“+”运算符号,“l11*l13”、“l12+l2”
>> syms l11 l13 l12 l2 l3 l5 l6 theta10 theta32 theta43 theta54 theta65
>> DH_TABLE = [l11*l13, 0, 0, theta10;
l12+l2 , 0, 0, 90;
l2 , 0, 0, theta32;
l3 , 0, 0, theta43;
0 , 0, 0, theta54;
l5 , 0, 0, theta65;
l6 , 0, 0, 0 ] % 具有加减乘除运算符号的DH参数矩阵
DH_TABLE =
[ l11*l13, 0, 0, theta10]
[ l2 + l12, 0, 0, 90]
[ l2, 0, 0, theta32]
[ l3, 0, 0, theta43]
[ 0, 0, 0, theta54]
[ l5, 0, 0, theta65]
[ l6, 0, 0, 0]
>> [Dof,A] = m_SigalMesu(DH_TABLE) % 通过参数矩阵获得DH矩阵
Dof =
7
A(:,:,1) =
[ cos(theta10), -sin(theta10), 0, l11*l13*cos(theta10)]
[ sin(theta10), cos(theta10), 0, l11*l13*sin(theta10)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,2) =
[ cos(90), -sin(90), 0, cos(90)*(l2 + l12)]
[ sin(90), cos(90), 0, sin(90)*(l2 + l12)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,3) =
[ cos(theta32), -sin(theta32), 0, l2*cos(theta32)]
[ sin(theta32), cos(theta32), 0, l2*sin(theta32)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,4) =
[ cos(theta43), -sin(theta43), 0, l3*cos(theta43)]
[ sin(theta43), cos(theta43), 0, l3*sin(theta43)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,5) =
[ cos(theta54), -sin(theta54), 0, 0]
[ sin(theta54), cos(theta54), 0, 0]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,6) =
[ cos(theta65), -sin(theta65), 0, l5*cos(theta65)]
[ sin(theta65), cos(theta65), 0, l5*sin(theta65)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
A(:,:,7) =
[ 1, 0, 0, l6]
[ 0, 1, 0, 0]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
>> T = simplify(A(:,:,1)*A(:,:,2)) % 计算0-1-2的转换关系
T =
[ cos(theta10 + 90), -sin(theta10 + 90), 0, cos(theta10 + 90)*(l2 + l12) + l11*l13*cos(theta10)]
[ sin(theta10 + 90), cos(theta10 + 90), 0, sin(theta10 + 90)*(l2 + l12) + l11*l13*sin(theta10)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
这便是通过建立符号矩阵的方式输入DH参数的优点所在!!!
4)、另外,我们在通过matlab获得DH矩阵,甚至进而得到转换矩阵之后;如果需要带入具体数值求值,则需要利用到subs()函数。
subs函数使用格式如下:
subs(表达式,表达式参数,表达式参数对应的新值)
如:求得0-1-2的转换矩阵,并将具体数值带入其矩阵中:
%%%% 获得0-1-2的转换矩阵
>> T = simplify(A(:,:,1)*A(:,:,2))
T =
[ cos(theta10 + 90), -sin(theta10 + 90), 0, cos(theta10 + 90)*(l2 + l12) + l11*l13*cos(theta10)]
[ sin(theta10 + 90), cos(theta10 + 90), 0, sin(theta10 + 90)*(l2 + l12) + l11*l13*sin(theta10)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
%%%% 将l12 = 2 带入T矩阵
>> t = subs(T,l2,2)
t =
[ cos(theta10 + 90), -sin(theta10 + 90), 0, cos(theta10 + 90)*(l12 + 2) + l11*l13*cos(theta10)]
[ sin(theta10 + 90), cos(theta10 + 90), 0, sin(theta10 + 90)*(l12 + 2) + l11*l13*sin(theta10)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
%%%% 将theta10 = 90°,l11 = 1,l12 = 2 ,l2 = 3,l3 = 0.5 带入T矩阵
>> t = subs(T,[theta10 l11 l12 l2 l3],[90 1 2 3 0.5])
t =
[ cos(180), -sin(180), 0, 5*cos(180) + l13*cos(90)]
[ sin(180), cos(180), 0, 5*sin(180) + l13*sin(90)]
[ 0, 0, 1, 0]
[ 0, 0, 0, 1]
注:本次利用到了matlab符号函数计算工具,具体的相关知识参考:
https://wenku.baidu.com/view/e488e5decc7931b764ce15c4.html
