深入理解word2vec的skip-gram模型（二）

上一篇文章我们了解skip-gram的输入层、隐层、输出层。在第二部分，会继续深入讲如何在skip-gram模型上进行高效的训练。

在第一部分讲解完成后，我们会发现Word2Vec模型是一个超级大的神经网络（权重矩阵规模非常大）。

举个栗子，我们拥有10000个单词的词汇表，我们如果想嵌入300维的词向量，那么我们的输入-隐层权重矩阵和隐层-输出层的权重矩阵都会有 10000 x 300 = 300万个权重，在如此庞大的神经网络中进行梯度下降是相当慢的。更糟糕的是，你需要大量的训练数据来调整这些权重并且避免过拟合。百万数量级的权重矩阵和亿万数量级的训练样本意味着训练这个模型将会是个灾难（太凶残了）。

Word2Vec的作者在它的第二篇论文中强调了这些问题，下面是作者在第二篇论文中的三个创新：
将常见的单词组合（word pairs）或者词组作为单个“words”来处理。
对高频次单词进行抽样来减少训练样本的个数。
对优化目标采用“negative sampling”方法，这样每个训练样本的训练只会更新一小部分的模型权重，从而降低计算负担。
事实证明，对常用词抽样并且对优化目标采用“negative sampling”不仅降低了训练过程中的计算负担，还提高了训练的词向量的质量。

Word pairs and “phases”

论文的作者指出，一些单词组合（或者词组）的含义和拆开以后具有完全不同的意义。比如“Boston Globe”是一种报刊的名字，而单独的“Boston”和“Globe”这样单个的单词却表达不出这样的含义。因此，在文章中只要出现“Boston Globe”，我们就应该把它作为一个单独的词来生成其词向量，而不是将其拆开。同样的例子还有“New York”，“United Stated”等。

在Google发布的模型中，它本身的训练样本中有来自Google News数据集中的1000亿的单词，但是除了单个单词以外，单词组合（或词组）又有3百万之多。

如果你对模型的词汇表感兴趣，可以点击这里，你还可以直接浏览这个词汇表。

如果想了解这个模型如何进行文档中的词组抽取，可以看论文中“Learning Phrases”这一章，对应的代码word2phrase.c被发布在这里。

对高频词抽样

在上一篇文章的讲解中，我们展示了训练样本是如何从原始文档中生成出来的，这里我再重复一次。我们的原始文本为“The quick brown fox jumps over the laze dog”，如果我使用大小为2的窗口，那么我们可以得到图中展示的那些训练样本。

但是对于“the”这种常用高频单词，这样的处理方式会存在下面两个问题：

• 当我们得到成对的单词训练样本时，(“fox”, “the”) 这样的训练样本并不会给我们提供关于“fox”更多的语义信息，因为“the”在每个单词的上下文中几乎都会出现。
• 由于在文本中“the”这样的常用词出现概率很大，因此我们将会有大量的（”the“，…）这样的训练样本，而这些样本数量远远超过了我们学习“the”这个词向量所需的训练样本数。
  Word2Vec通过“抽样”模式来解决这种高频词问题。它的基本思想如下：对于我们在训练原始文本中遇到的每一个单词，它们都有一定概率被我们从文本中删掉，而这个被删除的概率与单词的频率有关。
  如果我们设置窗口大小span=10（即skip_windows=5），并且从我们的文本中删除所有的“the”，那么会有下面的结果：
• 由于我们删除了文本中所有的“the”，那么在我们的训练样本中，“the”这个词永远也不会出现在我们的上下文窗口中。
• 当“the”作为input word时，我们的训练样本数至少会减少10个。
  这句话应该这么理解，假如我们的文本中仅出现了一个“the”，那么当这个“the”作为input word时，我们设置span=10，此时会得到10个训练样本 ("the", ...) ，如果删掉这个“the”，我们就会减少10个训练样本。实际中我们的文本中不止一个“the”，因此当“the”作为input word的时候，至少会减少10个训练样本。

上面提到的这两个影响结果实际上就帮助我们解决了高频词带来的问题。

抽样率

word2vec的C语言代码实现了一个计算在词汇表中保留某个词概率的公式。
${\omega }_i$是一个单词，$Z({\omega }_i)$是${\omega }_i$这个单词在所有语料中出现的频次。举个栗子，如果单词“peanut”在10亿规模大小的语料中出现了1000次，那么
$$Z{(}^{\prime }peanu{t}^{\prime })=1000/1000000000=1e-6$$
在代码中还有一个参数叫“sample”，这个参数代表一个阈值，默认值为0.001（在gensim包中的Word2Vec类说明中，这个参数默认为0.001，文档中对这个参数的解释为“ threshold for configuring which higher-frequency words are randomly downsampled”）。这个值越小意味着这个单词被保留下来的概率越小（即有越大的概率被我们删除）。
$P({\omega }_i)$代表着保留某个单词的概率：
$$P({\omega }_i)=(\sqrt{\frac{Z({\omega }_i)}{0.001}}+1)\times \frac{0.001}{Z({\omega }_i)}$$

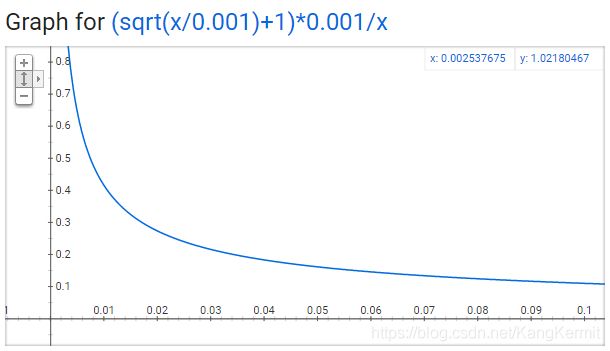
图中x轴代表着$Z({\omega }_i)$，即单词${\omega }_i$在语料中出现频率，y轴代表某个单词被保留的概率。对于一个庞大的语料来说，单个单词的出现频率不会很大，即使是常用词，也不可能特别大。

从这个图中，我们可以看到，随着单词出现频率的增高，它被采样保留的概率越来越小，我们还可以看到一些有趣的结论：

• 当$Z({\omega }_i)=0.0026$时，$P({\omega }_i)=1.0$。当单词在语料中出现的频率小于0.0026时，它是100%被保留的，这意味着只有那些在语料中出现频率超过0.26%的单词才会被采样。
• 当$Z({\omega }_i)=0.00746$时，$P({\omega }_i)=0.5$，意味着这一部分的单词有50%的概率被保留。
• 当$Z({\omega }_i)=1.0$时，$P({\omega }_i)=0.033$，意味着这部分单词以3.3%的概率被保留。
  如果你去看那篇论文的话，你会发现作者在论文中对函数公式的定义和在C语言代码的实现上有一些差别，但我认为C语言代码的公式实现是更权威的一个版本。

负采样（negative sampling）

训练一个神经网络意味着要输入训练样本并且不断调整神经元的权重，从而不断提高对目标的准确预测。每当神经网络经过一个训练样本的训练，它的权重就会进行一次调整。

正如我们上面所讨论的，vocabulary的大小决定了我们的Skip-Gram神经网络将会拥有大规模的权重矩阵，所有的这些权重需要通过我们数以亿计的训练样本来进行调整，这是非常消耗计算资源的，并且实际中训练起来会非常慢。

负采样（negative sampling）解决了这个问题，它是用来提高训练速度并且改善所得到词向量的质量的一种方法。不同于原本每个训练样本更新所有的权重，负采样每次让一个训练样本仅仅更新一小部分的权重，这样就会降低梯度下降过程中的计算量。

当我们用训练样本 ( input word: “fox”，output word: “quick”) 来训练我们的神经网络时，“ fox”和“quick”都是经过one-hot编码的。如果我们的vocabulary大小为10000时，在输出层，我们期望对应“quick”单词的那个神经元结点输出1，其余9999个都应该输出0。在这里，这9999个我们期望输出为0的神经元结点所对应的单词我们称为“negative” word。

当使用负采样时，我们将随机选择一小部分的negative words（比如选5个negative words）来更新对应的权重。我们也会对我们的“positive” word进行权重更新（在我们上面的例子中，这个单词指的是”quick“）。

在论文中，作者指出指出对于小规模数据集，选择5-20个negative words会比较好，对于大规模数据集可以仅选择2-5个negative words。

回忆一下我们的隐层-输出层拥有300 x 10000的权重矩阵。如果使用了负采样的方法我们仅仅去更新我们的positive word-“quick”的和我们选择的其他5个negative words的结点对应的权重，共计6个输出神经元，相当于每次只更新300X6=1800个权重。对于3百万的权重来说，相当于只计算了0.06%的权重，这样计算效率就大幅度提高。

如何选择negative words

我们使用“一元模型分布（unigram distribution）”来选择“negative words”。

要注意的一点是，一个单词被选作negative sample的概率跟它出现的频次有关，出现频次越高的单词越容易被选作negative words。

在word2vec的C语言实现中，你可以看到对于这个概率的实现公式。每个单词被选为“negative words”的概率计算公式与其出现的频次有关。
代码中的公式实现如下：
$$P({\omega }_i)=\frac{f({\omega }_i{)}^{\frac{3}{4}}}{{\sum }_{j=0}^n(f({\omega }_i{)}^{\frac{3}{4}})}$$
每个单词被赋予一个权重，即$f({\omega }_i)$， 它代表着单词出现的频次。
公式中开3/4的根号完全是基于经验的，论文中提到这个公式的效果要比其它公式更加出色。你可以在google的搜索栏中输入“plot y = x^(3/4) and y = x”，然后看到这两幅图（如下图），仔细观察x在[0,1]区间内时y的取值，$x^{frac34}$有一小段弧形，取值在$y=x$函数之上。

负采样的C语言实现非常的有趣。unigram table有一个包含了一亿个元素的数组，这个数组是由词汇表中每个单词的索引号填充的，并且这个数组中有重复，也就是说有些单词会出现多次。那么每个单词的索引在这个数组中出现的次数该如何决定呢，有公式$P({\omega }_i)\ast table\_size$，也就是说计算出的负采样概率*1亿=单词在表中出现的次数。

有了这张表以后，每次去我们进行负采样时，只需要在0-1亿范围内生成一个随机数，然后选择表中索引号为这个随机数的那个单词作为我们的negative word即可。一个单词的负采样概率越大，那么它在这个表中出现的次数就越多，它被选中的概率就越大。

到目前为止，Word2Vec中的Skip-Gram模型就讲完了，对于里面具体的数学公式推导细节这里并没有深入。这篇文章只是对于实现细节上的一些思想进行了阐述。

转载自：https://zhuanlan.zhihu.com/p/27234078

感谢阅读。