LightGBM 相关知识理解

lightGBM 简介

GBDT是个经典的模型，主要是利用弱分类器（决策树）迭代训练以得到最优模型，该模型具有训练效果好、不易过拟合等优点，常被用于多分类、点击率预测、搜索排序等任务。

在LightGBM提出之前，还有个GBDT的高效实现：XGBoost。XGBoost是属于boosting家族，也是GBDT算法的一个工程实现。 在模型的训练过程中是聚焦残差，在目标函数中使用了二阶泰勒展开并加入了正则，在决策树的生成过程中采用近似分割的方式（可以理解为分桶的思路），选出一些候选的分裂点，然后再遍历这些较少的分裂点，计算按照这些候选分裂点位分裂后的全部样本的目标函数增益，找到最大的那个增益对应的特征和候选分裂点位，从而进行分裂。这样一层一层的完成建树过程， XGBoost训练的时候，是通过加法的方式进行训练，也就是每一次通过聚焦残差训练一棵树出来， 最后的预测结果是所有树的加和表示。

对于上面的过程，不难发现时间复杂度和空间复杂度比较高：

1. 首先就是空间消耗很大，因为预排序的话既需要保存数据的特征值， 还得保存特征排序后的索引，毕竟这样后续计算分割点的时候快一些，但是这样就需要消耗训练数据两倍的内存。
2. 其次， 时间上也有很大的开销，在遍历每一个分割点的时候，都需要进行分裂增益的计算，消耗的代价大。

总的来说，XGBoost寻找最优分裂点的复杂度由下面三个因素构成：
$$特征数量\times 分裂点的数量\times 样本的数量$$
LightGBM（Light Gradient Boosting Machine）也是一个实现GBDT算法的框架，支持高效率的并行训练，并且具有更快的训练速度、更低的内存消耗、更好的准确率、支持分布式可以快速处理海量数据等优点。它主要对上面的三个因素分别优化，下面提到的1，直方图算法就是为了减少分裂点的数量， 2，单边梯度抽样算法就是为了减少样本的数量，3， 互斥特征捆绑算法就是为了减少特征的数量。 并且后面两个是Lightgbm的亮点所在。

直方图算法(Histogram algorithm)

基本思想

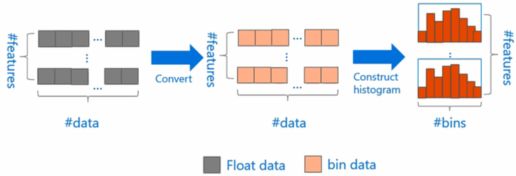
直方图算法的基本思想是：先把连续的浮点特征值离散化成 k 个整数，同时构造一个宽度为 k 的直方图。在遍历数据的时候，根据离散化后的值作为索引在直方图中累积计数，当遍历一次数据后，直方图累积了需要的统计量，然后根据直方图的离散值，遍历寻找最优的分割点。如下图所示：

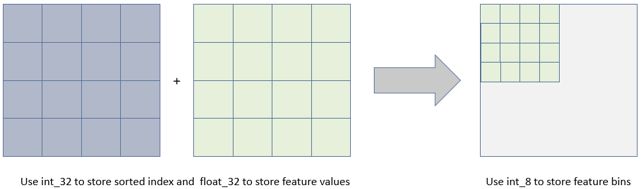
XGBoost 在进行预排序时只考虑非零值进行加速，而 LightGBM 也采用类似策略：只用非零特征构建直方图。这种离散化分桶思路其实有很多优点的， 首先最明显就是内存消耗的降低，XGBoost 需要用32位的浮点数去存储特征值， 并用32位的整型去存储索引：

而Lightgbm的直方图算法不仅不需要额外存储预排序的结果，而且可以只保存特征离散化后的值，而这个值一般用8位整型存储就足够了，即内存消耗从32+32变为了8，降低为原来的1/8。

同时，计数复杂度也大幅度降低，XGBoost的预排序算法每遍历一个特征值就需要计算一次分裂的增益，而Lightgbm直方图算法只需要计算k次（k可以认为是常数）：

时间复杂度从：
$$O((特征取值个数-1)\times 特征个数)$$
变为：
$$O((分桶数-1)\times 特征个数)$$
其中，特征取值个远大于分桶树。

直方图做差

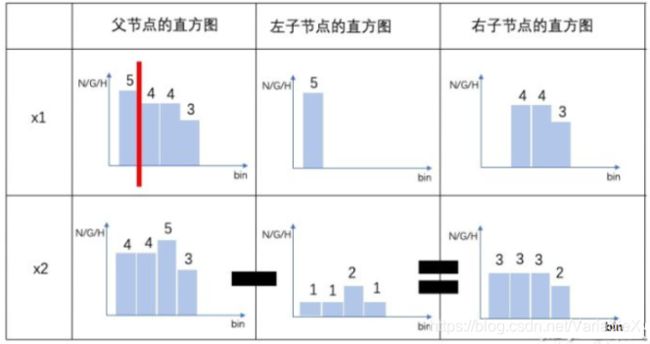
实际上，直方图算法还可以进一步加速。一般情况下，构造直方图需要遍历该叶子上的所有数据才行。但是对于二叉树而言，一个叶子节点的直方图可以直接由父节点的直方图和兄弟节点的直方图做差得到：

通过该方法，只需要遍历直方图的k个捅，速度提升了一倍。

举个例子，假设有15个训练样本，2个特征$x_1,x_2$, 然后我先对这两个特征进行分桶:

把$x_1$根据取值分成4个桶，每个桶里面的样本个数分别是5, 4, 4, 3。

把$x_2$根据取值也分成4个桶，每个桶里面的样本个数分别是4, 4, 5, 3。

然后我遍历特征，每个特征我遍历候选分割点(分桶后)，发现在$x_1$的第一个候选点那收益比较大，则第一个候选点进行分裂成两个节点。如下图所示 :

可以看到，直方图算法可以起到的作用就是可以减小分割点的数量， 加快计算。直方图算法并不是完美的。由于特征被离散化后，找到的并不是很精确的分割点，所以会对结果产生影响。但在实际的数据集上表明，离散化的分裂点对最终的精度影响并不大，甚至会好一些。原因在于决策树本身就是一个弱学习器，分割点是不是精确并不是太重要，采用直方图算法会起到正则化的效果，有效地防止模型的过拟合（分桶的数量决定了正则化的程度，分桶数越少惩罚越严重，欠拟合风险越高）。

XGBoost 使用的近似分割算法其实也有类似直方图算法的思想，但是他的分桶策略基于Weight Quantile Sketch算法，也就是基于二阶导的值 hi 来选择划分点。可以理解为所有样本都共享二阶导 hi 构成的直方图，一旦数据被分割，数据的分布就变了，导致 hi 的计算结果也发生变化，因此每次分裂都得重新构建直方图。

而对 lightgbm 而言，每个特征都有一个直方图，分裂后还能通过直方图做差来进行加速，因此速度要快于 XGBoost。

带深度限制的 Leaf-wise 算法

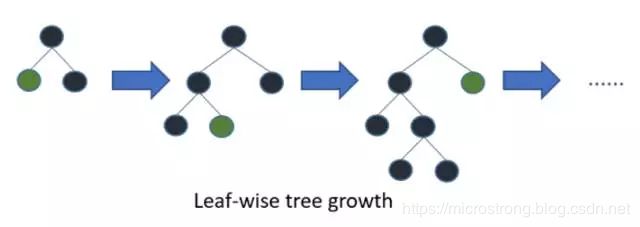
直方图算法，不仅有趣也很有效率。这还没有结束，在直方图算法之上，LightGBM进行进一步的优化。首先它抛弃了大多数GBDT工具使用的按层生长 (level-wise) 的决策树生长策略，而使用了带有深度限制的按叶子生长 (leaf-wise) 算法。

XGBoost 采用 Level-wise 的增长策略，该策略遍历一次数据可以同时分裂同一层的所有叶节点，容易进行多线程优化，也好控制模型复杂度，不容易过拟合。过程如下图所示：

但实际上Level-wise是一种低效的算法，因为它不加区分的对待同一层的叶子，实际上很多叶子的分裂增益较低，没必要进行搜索和分裂，因此带来了很多没必要的计算开销。

LightGBM采用Leaf-wise的增长策略，该策略每次从当前所有叶子中，找到分裂增益最大的一个叶子，然后分裂，如此循环。

因此同Level-wise相比，Leaf-wise的优点是：在分裂次数相同的情况下，Leaf-wise可以降低更多的误差，得到更好的精度；Leaf-wise的缺点是：可能会长出比较深的决策树，产生过拟合。因此LightGBM会在Leaf-wise之上增加了一个最大深度的限制，在保证高效率的同时防止过拟合。

单边梯度采样算法(GOSS)

我们观察到GBDT中每个数据都有不同的梯度值，即梯度小的样本，训练误差也比较小，说明数据已经被模型学习得很好了，直接想法就是丢掉这部分梯度小的数据。然而这样做会改变数据的分布，将会影响训练模型的精确度，为了避免此问题，提出了单边梯度抽样算法。

单边梯度抽样算法(Gradient-based One-Side Sampling)是从减少样本的角度出发， 排除大部分权重小的样本，仅用梯度大的样本和少数梯度小的样本计算信息增益，它是一种在减少数据和保证精度上平衡的算法。

具体来说，GOSS在进行数据采样的时候只保留了梯度较大的样本，对于梯度较小的样本，如果全部丢弃会影响数据的总体分布，因此需要对梯度小的样本进行采样。GOSS首先将要进行分裂的特征的所有取值按照绝对值大小降序排序，仅仅保存绝对值最大的 $a\ast 100\%$ 个数据。然后在剩下的较小梯度数据中随机选择 $b\ast 100\%$个数据。既然小梯度的样本数量比较少，那么可以给与样本更大的权重$\frac{1-a}{b}$，这样算法一方面会更关注训练不足的样本，另一方面不至于过多的改变原始数据集的分布。

算法流程如下：

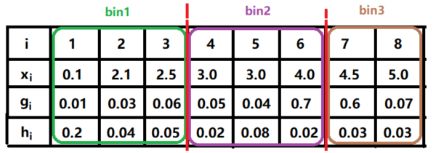
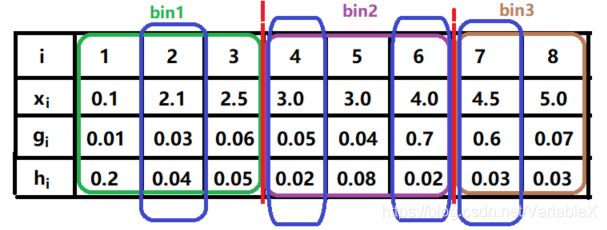
举个例子，假设 $a=\frac{1}{4}，b=\frac{1}{4}$，对于下面的数据：

对一阶导降序排序，得到：

然后选择 8*1/4=2 个梯度大的样本，再从剩下的 8 - 2=6 个小梯度样本中随机采样出 8*1/4=2 个，例如选出了2号和4号样本：

可以发现上面选择到的数据分布在不同的桶内：

对于采样得到的2号和4号样本，还需要乘上一个权重系数$\frac{1-a}{b}=3$，减少分布的变化，对于6号和7号样本则无需此操作。具体而言，这个系数是乘在样本个数、一阶导数和二阶导上的：

梯度小的样本乘上相应的权重之后，可以发现样本个数 $N_i$ 的总个数依然是8个， 虽然6个梯度小的样本中去掉了4个，留下了两个。 但是这2个样本在梯度上和个数上都进行了3倍的放大，所以可以防止采样对原数数据分布造成太大的影响， 这也就是论文里面说的将更多的注意力放在训练不足的样本上的原因。

通过这样的方式，在不过分降低精度的同时，减少了用于训练的样本数量，使得训练速度得到了加快。

互斥特征捆绑算法(EFB)

高维度的数据往往是稀疏的，这种稀疏性启发我们设计一种无损的方法来减少特征的维度。通常被捆绑的特征都是互斥的（即特征不会同时为非零值，像one-hot），这样两个特征捆绑起来才不会丢失信息。如果两个特征并不是完全互斥（部分情况下两个特征都是非零值），可以用一个指标对特征不互斥程度进行衡量，称之为冲突比率，当这个值较小时，我们可以选择把不完全互斥的两个特征捆绑，而不影响最后的精度。

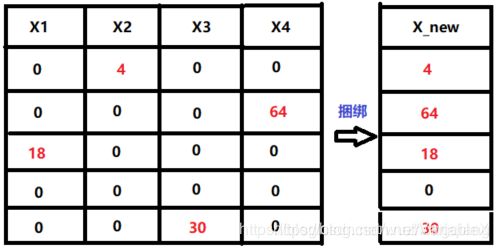
举个例子说明特征捆绑在做什么：

上图中原始数据的形式很类似于one-hot编码，可以将上面的4个特征捆绑到一起，达到减少特征维度的作用。上面的例子比较特殊，被捆绑的特征都是互斥的（即特征不会同时为非零值，像one-hot），这样两个特征捆绑起来才不会丢失信息。实际情况下，很多特征之间存在冲突(存在某个样本的两个特征同时不为零)，可以用一个指标对特征不互斥程度进行衡量，称之为冲突比率，当这个值较小时，我们可以选择把不完全互斥的两个特征捆绑，而不影响最后的精度。这样，构建直方图时的时间复杂度就从：
$$O(数据数量\times 特征数量)$$
变为：
$$O(数据数量\times 捆绑特征数量)$$
显然捆绑特征数量远少于特征数量，可以达到加速的效果。

说到这里，会遇到两个问题：

1. 怎么判定哪些特征应该绑在一起（build bundled）？
2. 怎么把特征绑为一个（merge feature）？

1，解决哪些特征应该绑在一起

LightGBM的EFB算法将这个问题转化为图着色的问题来求解，将所有的特征视为图的各个顶点，将不是相互独立的特征用一条边连接起来，边的权重就是两个相连接的特征的总冲突值，这样需要绑定的特征就是在图着色问题中要涂上同一种颜色的那些点（特征）。举个例子：

此外，我们注意到通常有很多特征，尽管不是100％相互排斥，但也很少同时取非零值。上面这个过程的时间复杂度其实是$O(特征{数}^2)$的，因为要遍历特征，每个特征还要遍历所有的簇， 在特征不多的情况下还行，但是如果特征维度很大，就不好使了。 所以为了改善效率，可以不建立图，而是将特征按照非零值个数进行排序，因为更多的非零值的特征会导致更多的冲突，所以跳过了上面的第一步，直接排序然后第三步分簇。

EFB 算法流程如下：

算法允许两两特征并不完全互斥来增加特征捆绑的数量，通过设置最大冲突比率 $\gamma$ 来平衡算法的精度和效率。

这样哪些特征捆绑的问题就解决了。

2，解决怎么把特征绑为一捆

特征合并算法，其关键在于原始特征能从合并的特征中分离出来。绑定几个特征在同一个bundle里需要保证绑定前的原始特征的值可以在bundle中识别，考虑到直方图算法将连续的值保存为离散的bins，我们可以使得不同特征的值分到bundle中的不同桶中，这可以通过在特征值中加一个偏置常量来解决。比如，我们在bundle中绑定了两个特征A和B，A特征的原始取值为区间 [0,10)，B特征的原始取值为区间[0,20)，我们可以在B特征的取值上加一个偏置常量101010，将其取值范围变为[10,30)，绑定后的特征取值范围为 [0,30)，这样就可以放心的融合特征A和B了。

例如对于特征A和B在1和2的部分有重叠，则可以通过“右移”特征B来避免重叠：

通过EFB，许多有少量冲突的特征就被捆绑成了更少的密集特征，这个大大减少的特征的数量，对训练速度又带来很大的提高。利用这种思路，可以通过对某些特征的取值重新编码，将多个这样互斥的特征捆绑成为一个新的特征。有趣的是，对于类别特征，如果转换成onehot编码，则这些onehot编码后的多个特征相互之间是互斥的，从而可以被捆绑成为一个特征。因此，对于指定为类别型的特征，LightGBM可以直接将每个类别取值和一个bin关联，从而自动地处理它们，而无需预处理成onehot编码。

具体的特征合并算法如下所示：

LightGBM的工程优化

1，原生支持类别特征

LightGBM 是原生支持类别变量的模型，其他的大多数模型例如LR，SVM等都需要先将类别特征利用独热编码转化为多维0/1特征再输入到模型。对于基于决策树的算法而言，不推荐使用独热编码，会存在下面的问题：

1. 产生切分不平衡问题。独热编码后，一种情况是0/1特征中1的占比特别少，即大部分都是0，无论这个特征多重要，乘以相应的占比后增益也是特别的小；另一种情况是0/1特征中1的占比特别多，即大部分都是1，这样的话这个特征的又没有明显的区分度。
2. 影响决策树学习。由于独热编码后，特征空间维度大幅度增加，样本将会被划分到零散的小空间内部。在这样的小空间内，会因为样本数量不足，统计信息不够准确，导致学习效果变差。

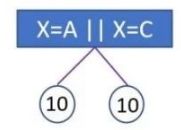
LightGBM 原生支持类别特征，采用 many-vs-many(每次将若干个类作为正类，若干个其他类作为负类) 的切分方式将类别特征分为两个子集，实现类别特征的最优切分。

例如当$X=A||X=C$时，放到左孩子，不符合条件的放到右孩子。数据会被切分到两个比较大的空间，进一步的学习也会更好。

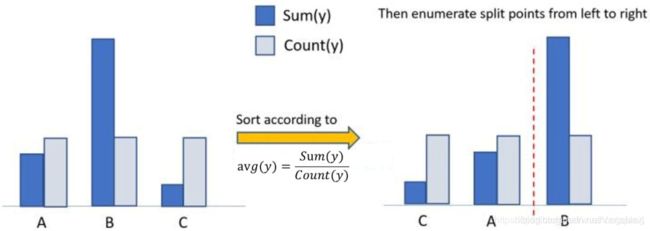
具体而言，在枚举类别变量的分割点之前，先把直方图按照每个类别对应的所有样本的label计算均值($\frac{sum(y)}{count(y)}$)，然后进行排序：

最后按照排序的结果依次枚举最优分割点。这个方法很容易过拟合，所以LightGBM里面还增加了很多对于这个方法的约束和正则化。 实验结果证明，这个方法可以使训练速度加速8倍。

2，高效并行

LightGBM支持三个角度的并行：特征并行，数据并行和投票并行。 下面我们一一来看看：

特征并行

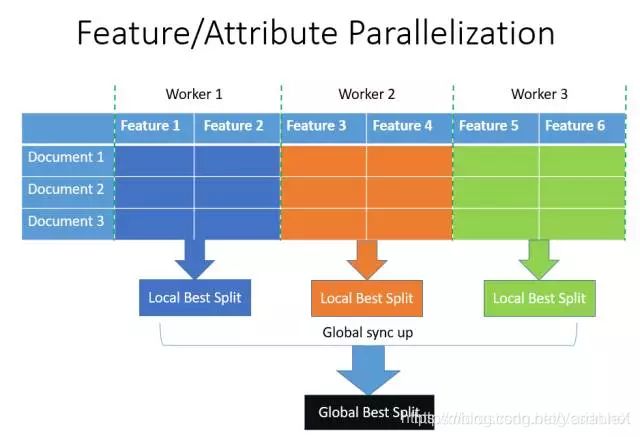
特征并行的主要思想是：不同机器在不同的特征子集上分别寻找最优的分割点，然后在机器间同步最优的分割点。XGBoost使用的就是这种特征并行方法。这种特征并行方法有个很大的缺点：就是对数据进行垂直划分，每台机器所含数据不同，然后使用不同机器找到不同特征的最优分裂点，划分结果需要通过通信告知每台机器，增加了额外的通信和同步上的复杂度。

LightGBM 则不进行数据垂直划分，而是在每台机器上保存全部训练数据，在得到最佳划分方案后可在本地执行划分而减少了不必要的通信。具体过程如下图所示。

数据并行

传统的数据并行策略主要为水平划分数据，让不同的机器先在本地构造直方图，然后进行全局的合并，最后在合并的直方图上面寻找最优分割点。这种数据划分有一个很大的缺点：通讯开销过大。如果使用点对点通信，一台机器的通讯开销大约为：
$$O(机器数量\ast 特征数量\ast 分桶数量)$$
如果使用集成的通信，则通讯开销为：
$$O(2\ast 特征数量\ast 分桶数量)$$
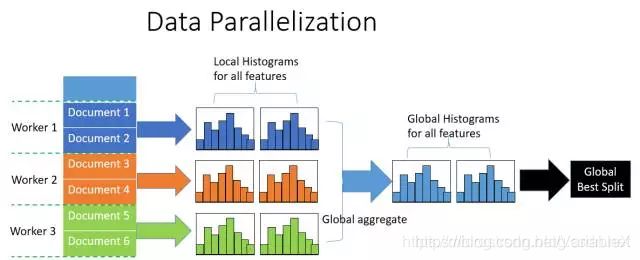
LightGBM在数据并行中使用分散规约 (Reduce scatter) 把直方图合并的任务分摊到不同的机器，降低通信和计算，并利用直方图做差，进一步减少了一半的通信量。具体过程如下图所示：

投票并行

基于投票的数据并行进一步优化数据并行中的通信代价，使得通信代价为常数级别。具体而言，该方法只合并部分特征的直方图从而达到降低通信量的目的，可以得到非常好的加速效果。具体过程如下图所示。大致步骤为两步：

1. 本地找出 Top K 特征，并基于投票筛选出可能是最优分割点的特征；

2. 合并时只合并每个机器选出来的特征。

3，Cache命中率优化

XGBoost对cache优化不友好，如下图所示。在预排序后，特征对梯度的访问是一种随机访问，并且不同的特征访问的顺序不一样，无法对cache进行优化。同时，在每一层长树的时候，需要随机访问一个行索引到叶子索引的数组，并且不同特征访问的顺序也不一样，也会造成较大的cache miss。

LightGBM 所使用直方图算法对 Cache 天生友好：

1. 首先，所有的特征都采用相同的方式获得梯度（区别于XGBoost的不同特征通过不同的索引获得梯度），只需要对梯度进行排序并可实现连续访问，大大提高了缓存命中率；

2. 其次，因为不需要存储行索引到叶子索引的数组，降低了存储消耗，而且也不存在 Cache Miss的问题。

LightGBM的优缺点

优点

这部分主要总结下 LightGBM 相对于 XGBoost 的优点，从内存和速度两方面进行介绍。

(1) 速度更快：

• LightGBM 采用了直方图算法将遍历样本转变为遍历直方图，极大的降低了时间复杂度；
• LightGBM 在训练过程中采用单边梯度算法过滤掉梯度小的样本，减少了大量的计算；
• LightGBM 采用了基于 Leaf-wise 算法的增长策略构建树，减少了很多不必要的计算量；
• LightGBM 采用优化后的特征并行、数据并行方法加速计算，当数据量非常大的时候还可以采用投票并行的策略；
• LightGBM 对缓存也进行了优化，增加了缓存命中率；

(2) 内存更小：

• LightGBM 采用了直方图算法将存储特征值转变为存储 bin 值，且不需要特征值到样本的索引，降低了内存消耗；
• LightGBM 在训练过程中采用互斥特征捆绑算法减少了特征数量，降低了内存消耗。

缺点

• 可能会长出比较深的决策树，产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度限制，在保证高效率的同时防止过拟合；
• Boosting族是迭代算法，每一次迭代都根据上一次迭代的预测结果对样本进行权重调整，所以随着迭代不断进行，误差会越来越小，模型的偏差（bias）会不断降低，所以会对噪点较为敏感；
• 在寻找最优解时，依据的是最优切分变量，没有将最优解是全部特征的综合这一理念考虑进去；

参考文章

1. 深入理解LightGBM

2. 白话机器学习算法理论+实战番外篇之LightGBM