自然语言处理——隐马尔可夫模型(HMM)及中文分词器
隐马尔可夫模型
- 概念基础
- 从马尔可夫假设到隐马尔可夫模型
- 隐马尔可夫模型的三要素
- 隐马尔可夫模型的训练
- 隐马尔科夫模型的预测
- 基于HHM的简单中文分词器
概念基础
从马尔可夫假设到隐马尔可夫模型
马尔可夫假设是指:每一个时间的发生概率只取决于前一个时间。当将满足该假设的多个事件串联在一起时,构成马尔可夫链。
而在自然语言的情景下,满足假设的连续的多个事件可以具象为单词,即马尔可夫模型具象为二元语法模型。
由此可得隐马尔可夫模型的两个假设:
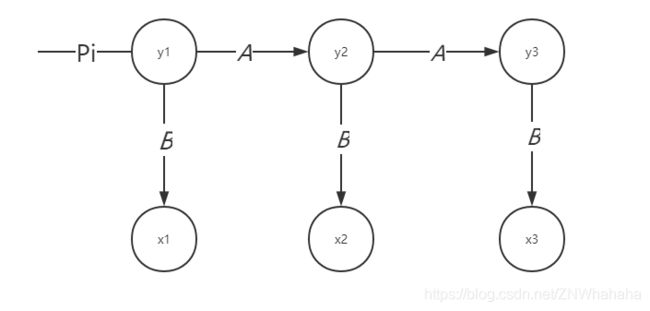
设 yi 为i时刻的一个状态节点。xi 为i时刻状态 yi 所对应的观测节点。
假设1:当前状态y t 仅仅依赖于前一个状态 yt-1 ,连续多个状态构成隐马尔可夫链y
假设2:任意时刻的观测xt只依赖于当前状态yt,与其他时刻的状态或者观测无关。

隐马尔可夫模型可以总结为先有状态,后有观测。
隐马尔可夫模型的三要素
隐马尔可夫模型的三要素有:初始状态概率向量 π \pi π、状态转移概率矩阵A、发射概率矩阵B。
初始状态概率向量:系统启动时进入的第一个状态y1称为初始状态,假设y有N种取值,那么y1就是一个独立的离散型随机变量,由p(y1| π \pi π) 描述。其中: π = ( p i 1 , . . . π N ) T , 0 ⩽ π i ⩽ 1 , ∑ i = 1 N π = 1 \pi= (pi_{1},... \pi_{N})^T, 0\leqslant \pi_{i}\leqslant 1,\sum_{i=1}^N \pi = 1 π=(pi1,...πN)T,0⩽πi⩽1,i=1∑Nπ=1
是概率分布的参数向量,称为初始状态概率向量。
状态转移概率矩阵:t+1时的状态仅仅取决于t时的状态,且一共有N种状态,则从状态si到sj的概率就构成了一个N×N的矩阵,称为状态转移概率矩阵。其实际意义是在中文分词当中,标签B后面不可能是S,通过赋值 p ( y t + 1 = S ∣ y t = B ) = 0 p(y_{t+1} = S| y_{t} = B) = 0 p(yt+1=S∣yt=B)=0就可以模拟这种禁止转移的需求。且这些参数不需要程序员手动服务,通过语料库学习可获得。
发射频率矩阵:假设观测x一共有M种可能的取值,则x的概率发布参数向量维数为M。由于y一共有N种,则这些参数向量构成 N × M N×M N×M的矩阵,则 B = [ p ( x t = o i ∣ y t = s j ) ] N × M B = [p(x_{t} = o_{i} | y_{t} = s_{j})]_{N×M} B=[p(xt=oi∣yt=sj)]N×M称为发射概率矩阵。概率发射矩阵的实际意义是通过赋予位置构成比较固定的字符相应的概率,防止一些词汇被错误切分。
隐马尔可夫模型的训练
隐马尔可夫模型的训练需要利用极大似然法估计其模型参数,即:转移概率矩阵的估计、初始状态概率向量的估计、发射概率矩阵的估计。
估计转移概率矩阵:记样本序列在时刻 t t t 处于状态 s i s_{i} si ,时刻 t + 1 t+1 t+1 转移到状态 s j s_{j} sj 。统计频次计入矩阵元素 A i , j A_{i,j} Ai,j ,根据极大似然估计,从 s i s_{i} si 到 s j s_{j} sj 的转移概率 a i , j a_{i,j} ai,j 可估计为矩阵第 i i i 行的归一化: a ^ i , j = A i , j ∑ j = 1 N , i , j = 1 , 2 , . . . , N \widehat{a}_{i,j} = \frac{A_{i,j}}{\sum_{j=1}^N} ,\quad\quad i,j = 1,2, ...,N a i,j=∑j=1NAi,j,i,j=1,2,...,N
估计初始状态概率向量:初始状态是状态转移的一种特例,且转移频次只有一行。统计 y 1 y_{1} y1 的所有取值的频次记为向量 c c c ,然后归一化: π ^ i = c i ∑ i = 1 N c i i = 1 , 2 , . . . , N \widehat{\pi}_{i} =\frac{c_{i}}{\sum_{i=1}^Nc_{i}}\quad\quad i=1,2 ,...,N π i=∑i=1Ncicii=1,2,...,N
估计发射概率矩阵:统计样本中状态为 s i s_i si 且观测为 o j o_j oj 的频次,计入矩阵元素 B i , j B_{i,j} Bi,j 中,则状态 s i s_i si 发射观测 o j o_j oj 的概率估计为: b ^ i , j = B i , j ∑ j = 1 M B i , j i = 1 , 2 , . . . , M \widehat{b}_{i,j}=\frac{B_{i,j}}{\sum_{j=1}^MB_{i,j}}\quad\quad i=1,2,...,M b i,j=∑j=1MBi,jBi,ji=1,2,...,M
结合以上三个公式,即可实现隐马尔科夫模型的样本生成和模型训练算法。
注意:在编写程序的过程中尽量取对数运算。即使用加法代替乘法,防止浮点数下溢出。
隐马尔科夫模型的预测
隐马尔科夫模型的预测分为两个步骤与算法:概率计算的向前算法与搜索状态序列的维特比算法。
概率计算的向前算法:主要解决给定观测序列 x x x 和一个状态序列 y y y ,估计两者的联合概率 p ( x , y ) p(x,y) p(x,y) 的问题。
如图二所示, t = 1 t=1 t=1 时初始状态没有前驱状态,发生概率由 π \pi π 决定,即: p ( y 1 = s i ) = π i p(y_1 = s_i)=\pi_i p(y1=si)=πi
对于 t ⩾ 2 t\geqslant 2 t⩾2 ,状态 y t y_t yt 由前驱状态 y t − 1 y_{t-1} yt−1 转移而来,其转移概率由矩阵 A A A决定,即: p ( y t = s j ∣ y t − 1 = s i ) = A i , j p(y_t = s_j|y_{t-1}=s_i) = A_{i,j} p(yt=sj∣yt−1=si)=Ai,j
则状态序列的概率为上两式的乘积,即: p ( y ) = p ( y 1 , . . . , y T ) = p ( y 1 ) ∏ t = 2 T p ( y t ∣ y t − 1 ) ( 公式一) p(y)=p(y_1, ... ,y_T)=p(y_1)\prod_{t=2}^Tp(y_t|y_{t-1})\tag { 公式一} p(y)=p(y1,...,yT)=p(y1)t=2∏Tp(yt∣yt−1)( 公式一)
对于1每一个 y t = s i y_t = s_i yt=si ,都会发射一个 x t = o j x_t=o_j xt=oj ,发射概率由矩阵 B B B 决定,即: p ( x t = o j ∣ y t = s i ) = B i , j p(x_t = o_j|y_t =s_i) =B_{i,j} p(xt=oj∣yt=si)=Bi,j
则给定长 T T T 的状态序列 y y y ,对应 x x x 的概率为上式的累积式,即: p ( x ∣ y ) = ∏ t = 1 T p ( x t ∣ y t ) ( 公式二) p(x|y) =\prod_{t=1}^Tp(x_t|y_t)\tag { 公式二} p(x∣y)=t=1∏Tp(xt∣yt)( 公式二)
公式一与公式二相乘得显隐状态序列的联合概率,即: p ( x ∣ y ) = p ( y ) p ( x ∣ y ) = p ( y 1 ) ∏ t = 2 T p ( y t ∣ y t − 1 ∏ t = 1 T p ( x t ∣ y t ) ) p(x|y) =p(y)p(x|y) \\=p(y_1)\prod_{t=2}^Tp(y_t|y_{t-1}\prod_{t=1}^Tp(x_t|y_t)) p(x∣y)=p(y)p(x∣y)=p(y1)t=2∏Tp(yt∣yt−1t=1∏Tp(xt∣yt))
综合以上数学公式,将其中的每个 x t , y t x_t,y_t xt,yt 对应的实际发生序列 s i , o j s_i,o_j si,oj ,就可带入 ( π , A , B ) (\pi,A,B) (π,A,B) 中的相应元素,从而计算出任意概率。
搜索状态序列的维特比算法:将每个状态作为有向图中的一个节点,节点间的距离由转移概率决定,节点本身花费由发射概率决定,则所有备选状态构成一幅有向无环图,待求的概率最大的状态徐磊就是有向无环图中的最长路径。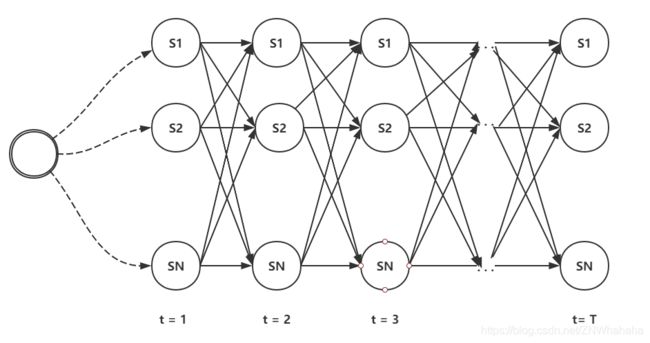
(1)初始化, t = 1 t=1 t=1 时初始最优路径的备选由 N N N 个状态组成,他们的前驱1为空。 δ 1 , i = π i B i , 0 1 , i = 1 , . . . , N \delta _{1,i} = \pi_iB_{i,0_1},\quad\quad i=1, ... ,N δ1,i=πiBi,01,i=1,...,N ψ 1 , i = 0 , i = 1 , . . . , N \psi_{1,i} = 0,\quad\quad i = 1, ... ,N ψ1,i=0,i=1,...,N
(2)递推, t ⩾ 2 t\geqslant2 t⩾2 时,每条备选路径吃入一个新状态,长度增加一个单位,根据转移概率和发射概率计算花费。找出新的局部最优路径,更新两个数组。 δ t , i = max 1 ⩽ j ⩽ N ( δ t − 1 , j A j , i ) B i , o t \delta_{t,i}=\max_{1\leqslant j \leqslant N}(\delta_{t-1,j}A_{j,i})B_{i,o_t} δt,i=1⩽j⩽Nmax(δt−1,jAj,i)Bi,ot ψ t , i = arg max 1 ⩽ j ⩽ N ( δ t − 1 , j A j , i ) \psi_{t,i}=\arg \max_{1\leqslant j \leqslant N}(\delta_{t-1,j}A_{j,i}) ψt,i=arg1⩽j⩽Nmax(δt−1,jAj,i)
(3)终止,找出最终时刻 δ t , i \delta_{t,i} δt,i 数组中的最大概率 p ∗ p^* p∗ ,以及相应的结尾状态下标 i T ∗ i_T^* iT∗ 。 p ∗ = max 1 ⩽ i ⩽ N δ T , i p^*=\max_{1\leqslant i \leqslant N}\delta_{T,i} p∗=1⩽i⩽NmaxδT,i i T ∗ = arg max 1 ⩽ i ⩽ N δ T , i i_T^*=\arg\max_{1\leqslant i \leqslant N}\delta_{T,i} iT∗=arg1⩽i⩽NmaxδT,i
(4)回溯,根据前驱数组 ψ \psi ψ 回溯前驱状态,取得最优路径状态下标 i ∗ = i 1 ∗ , . . . , i T ∗ i^* =i_1^*, ... ,i_T^* i∗=i1∗,...,iT∗ 。 i t ∗ = ψ t + 1 , i t + 1 ∗ , t = T − 1 , T − 2 , . . . , 1 i_t^* =\psi_{t+1,i_{t+1}^*},\quad\quad t = T-1,T-2, ... ,1 it∗=ψt+1,it+1∗,t=T−1,T−2,...,1
基于HHM的简单中文分词器
简单中文分词器