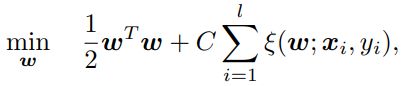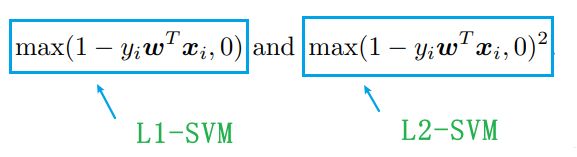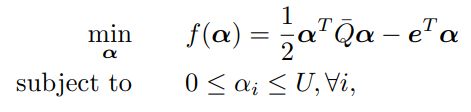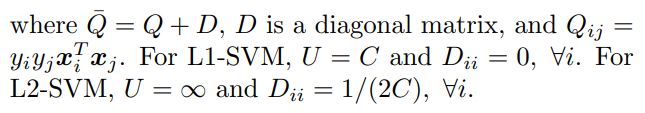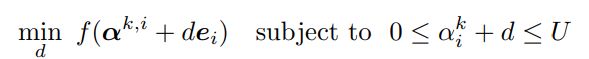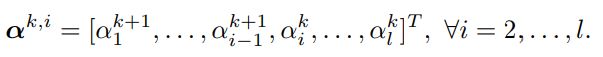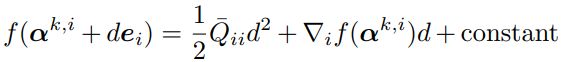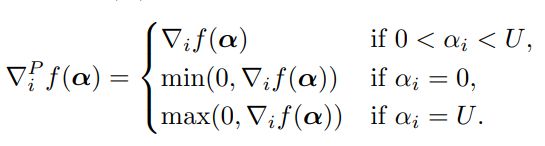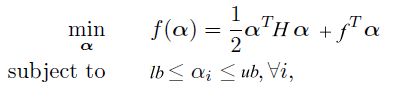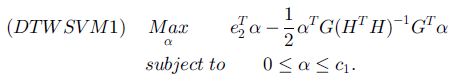DCDM ( Dual Coordinate Descent Method )：对偶坐标下降法的Matlab实现

目录

1. C-SVM 

算法流程

2. 求解二次规划 

3. TSVM

---

用对偶坐标下降法求解 SVM 的部分模型 

1. C-SVM 

实现《 A Dual Coordinate Descent Method for Large-scale Linear SVM 》论文[1]中的L1-SVM

原问题

其中，是损失函数，有两个比较相似的损失函数，这里定义两种SVM，当使用不同的损失函数时：

对偶问题

算法流程

DCDM共有两层循环，每一个外层循环都要产生一个alpha向量；内层循环从 1 到 n （alpha的维度），一次只更新alpha的一个元素，固定其他元素。一次内层循环求解一个单变量的子问题：

k 表示第 k 次外层循环，i 表示第 i 次内层循环。前 i-1 个 alpha 的元素已经更新了。

转化为：

下面求解这个二次函数：

令是投影梯度，且

如果则不用更新；

如果，则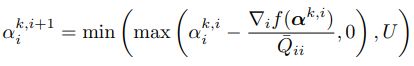，二次函数的极值点是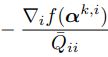，然后进行更新元素，并且保证在约束范围内。

---

这里给出 C-SVM 即 论文中的 L1-SVM 的实现

P.s.：内层循环更新元素时，可以顺序选取也可以随机选取。

% 对偶坐标下降法 dual coordinate descent method
% 以求解C-SVM为例
clear;clc
data = load('Pima.mat');
X = data.X1;Y = data.Y1;
X = [X ones(size(Y))];
X = X';
[~,n] = size(X); % n个样本
c = 2; % 模型中的平衡参数
iter = 10000; % 最大迭代次数
eps = 1e-14;
% rng(2);
alpha = rand(size(Y));
w = X*diag(Y)*alpha;
Q = diag(X'*X); % 取对角线的元素
% DCDM
k = 0;
count = 0;
tic;
% 停止准则：在一次外循环中所有的alpha都没有更新 或 达到最大迭代次数
while count eps
            alpha(i) = min(max(alpha(i)-G/Q(i),0),c);
            w = w+(alpha(i)-alpha_(i))*Y(i)*X(:,i);
        else
            count = count+1; % 记录一次外循环没有更新的变量的个数
        end    
    end
    k = k+1; 
end
t = toc;
% quadprog求解
H = diag(Y)*X'*X*diag(Y);
f = -ones(size(Y));
lb = zeros(size(Y));
ub = c*ones(size(Y));
alphaQ = quadprog(H,f,[],[],[],[],lb,ub);
wQ = X*diag(Y)*alphaQ;
% quadprog 与 DCDM 得到的结果对比
stem(wQ-w);
figure
stem(alphaQ-alpha);

---

 2020.8.22 补充 TSVM [2] 的 DCDM 求解

2. 求解二次规划 

function alpha = DCDM(H,f,lb,ub,n,eps,iter)
% 本函数求解 1/2*alpha'*H*alpha-e'*alpha
% e 是全 1 的向量
% lb,ub 变量的范围
% n 是 alpha 元素的个数
% eps 是一个极小的数
% iter 是最大迭代次数
rng(2);
alpha = rand(n,1);
% DCDM
k = 0;
count = 0;
tic;
% 停止准则：在一次外循环中所有的alpha都没有更新 或 达到最大迭代次数
while count eps
            alpha(i) = min(max(alpha(i)-G/H(i,i),lb),ub);
        else
            count = count+1; % 记录一次外循环没有更新的变量的个数
        end    
    end
    k = k+1 
end
t = toc;

3. TSVM

原问题

对偶问题

调用 2 中的 DCDM 函数求解 

%% TSVM
clear;clc
data = load('Pima.mat');
X = data.X5;Y = data.Y5;
A = X(Y==1,:);[n1,m] = size(A);
B = X(Y==-1,:);[n2,~] = size(B);
e1 = ones(n1,1);
e2 = ones(n2,1);
c = 4;
iter = 20000; % 最大迭代次数
eps = 1e-8;

%%% 正类超平面
Gt = [B e2];Ht = [A e1];
H1 = Gt/(Ht'*Ht)*Gt';
lb = 0;ub = c;
% DCDM 
alpha = DCDM(H1,-e2,lb,ub,n2,eps,iter);
u = -(Ht'*Ht)\Gt'*alpha;
% quadprog
alphaQ = quadprog(H1,-e2,[],[],[],[],zeros(n2,1),c*ones(n2,1));
uQ = -(Ht'*Ht)\Gt'*alphaQ;
% 作图比较
subplot(221)
stem(alphaQ-alpha);
subplot(222)
stem(u-uQ)

%%% 负类超平面
Pt = [A e1];Qt = [B e2];
H2 = Pt/(Qt'*Qt)*Pt';
lb = 0;ub = c;
% DCDM
beta = DCDM(H2,-e1,lb,ub,n1,eps,iter);
v = (Qt'*Qt)\Pt'*beta;
% quadprog
betaQ = quadprog(H2,-e1,[],[],[],[],zeros(n1,1),c*ones(n1,1));
vQ = (Qt'*Qt)\Pt'*betaQ;
% 作图比较
subplot(223)
stem(beta-betaQ)
subplot(224)
stem(v-vQ);

%%% 测试
tstX = data.tstX5;tstY = data.tstY5;
[m0,~] = size(tstX);

% DCDM
d1 = abs([tstX ones(m0,1)]*u); % calss 1
d2 = abs([tstX ones(m0,1)]*v); % class -1
y = zeros(m0,1);
y(d1d2) = -1;
real = sum(tstY==y);
accuracy = real/m0;

% quadprog
d11 = abs([tstX ones(m0,1)]*uQ); 
d22 = abs([tstX ones(m0,1)]*vQ); 

y1 = zeros(m0,1);
y1(d11d22) = -1;
real1 = sum(tstY==y1);
accuracy1 = real1/m0;

 

 

参考资料：

[1] Hsieh C J , Chang K W , Lin C J , et al. A Dual Coordinate Descent Method for Large-scale Linear SVM[C]// In ICML 2008. 2008.

[2] Jayadeva, Khemchandani R , Chandra S . Twin Support Vector Machines for Pattern Classification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29:905-910.