【转】图解张量_Tensor(数学不行还学AI-第4话)
看了很多tensor的介绍文章,感觉这篇是最通俗易懂的。
转载:https://zhuanlan.zhihu.com/p/25268020
原文: Learning AI if You Suck at Math — P4 — Tensors Illustrated (with Cats!)
在线运行代码版:数学不行还学AI-第4话-图解张量(内有恶猫) - 集智专栏
作者:Daniel Jeffries
翻译/注释:Kaiser(王司图)
前言
昨天翻译了一篇用Keras识别AV女优的文章,虽然反响很热烈,但是很多朋友反映看不懂。其实那篇文章自身就不是特别完备,只是提供个大概思路,并不能逐步复现。所以今天来一篇相对简单、通俗的。
读者朋友们可能奇怪,为什么一上来就是“第4话”。 这是一个连载中的系列文章,题为Learning AI if You Suck at Math,一听就很丧。北邮陈老师(爱可可-爱生活)翻译为“数学菜鸟的AI学习攻略”,这太正能量了不够丧。所以我翻译为“数学不行还学AI”。
此处的“还”字语气应模仿周星驰在《功夫》里的“还踢球!”。
原作者Daniel Jeffries是一位科幻作家,他的新书见下图微博中我的评论,为防“政治敏感”罪名,我就不翻译了(当然,在我自己的网站上,我翻译了)。看他写作的风格(可以说是魔幻了)就可以理解,为什么文章标题一定要翻译的丧。
本系列的前三篇没有翻译的原因是这样的:
第一篇:Learning AI if You Suck at Math 抒情居多,后面推荐了几本数学方面的书籍。感兴趣的朋友可以点击原文查看,因为推荐的都是英文书,所以翻译过来也没有太大价值。
第二篇:Learning AI if You Suck at Math — Part Two — Practical Projects ,作家就是作家,仍然是抒情成分居多,然后介绍了一下Kaggle竞赛以及Keras+TensorFlow框架。
第三篇:Learning AI if You Suck at Math — P3 — Building an AI Dream Machine or Budget Friendly Special,终于不抒情了,这是一篇攒机和开发环境配置的攻略。硬件方面,作者的推荐与我国国情有一定偏差。开发环境配置方面,我已经在集智的后台做好了,读者可以直接在网页上运行Python代码,免除了最麻烦的部分。
不管是知乎还是StackOverflow,几乎所有编程版块的问题,都有一大半是关于安装、配置的。而云计算已经很普及,实在想在本地搭建也可以用docker解决,我觉得没有必要在繁琐的配置上浪费太多时间。
以上三篇可以说是撩拨的前戏,本篇《图解张量(内有恶猫!)》终于直奔主题顶到了花心。
正文
可能你已经下载TensorFlow并且准备好开始深度学习了。
但你可能会问:什么他妈的叫他妈的Tensor? (What the hell is a tensor?)
或许你已经看过了维基百科页面 ,然后你更加迷茫了。又可能你看过了了这个NASA tutorial但还是不知道这说了些什么? 你像陈绮贞老师,收集书本里每一句你最爱的真理。
问题的关键在于,大多数教程在谈及Tensor的时候,都预设你已经懂得了所有描述性的数学语言。
不要怕!
我想很多孩子一样讨厌数学,所以要是连我都能能懂,那你也可以!我们只需要用最简单的方式来解释一切。
所以到底什么他妈的叫他妈的Tensor,它又怎么就Flow了?
Tensors = Containers(张量是个筐)
张量(tensor)是现代机器学习的最基础元素。
本质上来讲,张量就是个数据容器。多数情况下盛的是数字,有时也会盛字符但比较少。
所以不妨把它想象成一筐数字 。(So think of it as a bucket of numbers. bucket原意是“桶”,但中文还是“筐”用的比较多。比如“国情是个筐”,而没有说“国情是个桶”的。)
张量就像避孕套,有不同的型号(这个比喻是Kaiser自创的)。来一起认识一下你在深度学习中将会遇到的基本款——0维到5维。
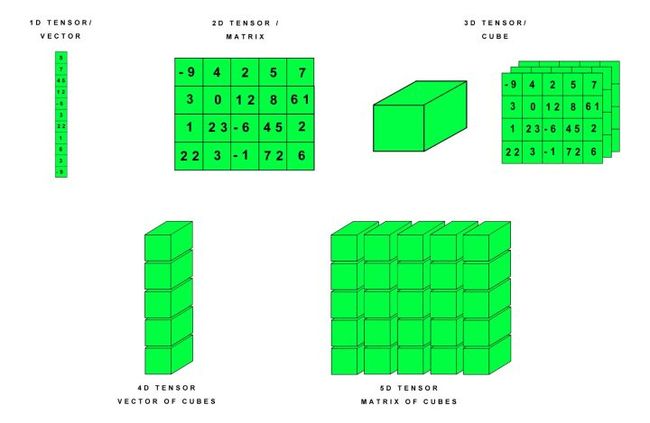
我们可以把这些张量做如下可视化(猫?在后面!)
0维张量/标量
张量这个筐里的一个数字就叫标量(scalar)。
一个标量就是一个数字。
你可能会问,为什么不直接叫数字?
我也不知道,可能数学家们觉得这样挺起来比较屌?(并没有)
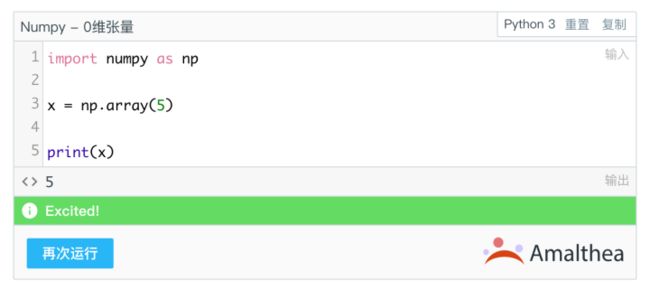
实际上你可以拥有只含一个数字的张量,这就是0维张量,好比一个筐里只有一滴水(已经好过“竹篮子打水一场空”了)。
在本教程中我们将使用Python, Keras和TensorFlow以及NumPy,这些环境已经在集智中搭建好了。
在Python中,张量一般表示为Numpy数组。 NumPy 是一个科学计算库, 你球基本上所有AI框架都用到了NumPy。
在数据科学竞赛网站Kaggle上,你经常可以看到Jupyter Notebooks(本站的在线开发环境也是基于Jupyter Notebooks)提到把数据转换为Numpy数组。Jupyter Notebook集成了文档与代码功能,融讲解和编程于一体。
为什么要把数据转换为Numpy数组?
很简单,因为我们需要应对各种各样的输入数据——字符、图像、股价或者视频——整合到一个标准下。
这种情况下,我们把数据塞进“数字筐”(张量)里,才能通过TensorFlow操纵它们。
其实就是把数据组织成一种可用的格式。在网络编程中,你可能用XML来呈现(微信就是),所以你可以快捷地定义和操纵数据。同样的,深度学习中我们使用张量这个筐来作为乐高里最小的零件。
1维张量/矢量
如果你是程序员,那你应该已经知道一种跟1维张量很接近的东西:数组。
每个编程语言都有数组,其实就是一行或一列数据。在深度学习中称作1维张量,张量可以根据轴的数量来定义,1维张量就只有一个数轴。
1维张量是矢量(vector)。
我们可以把矢量可视化为一行或一列数字。
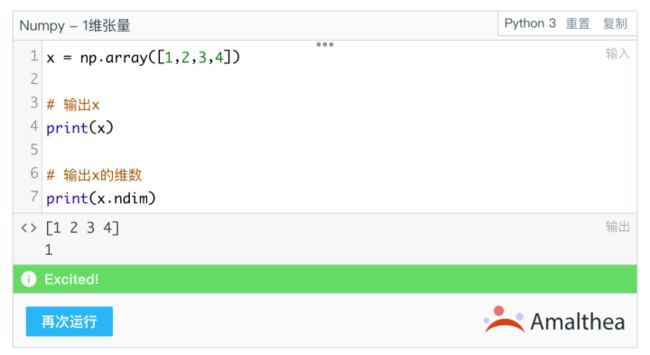
如果想在Numpy中查看,可执行如下操作:
也可以用Numpy的ndim输出张量的维数。
2维张量
你大概已经想到了另一种张量:矩阵
2维向量是矩阵(matrix)。
不,不是基努里维斯那个电影,是类似Excel表格的这样一个数据结构。
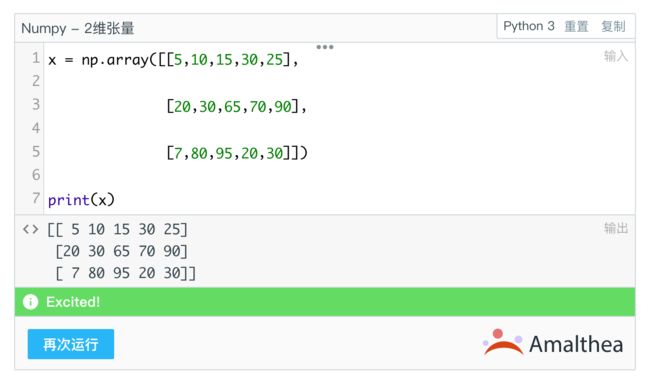
我们可以将其可视化为有行/列的数字网格。
行和列代表了两个轴,矩阵是2维张量。在NumPy中我们可以如此表示:
我们可以把人物属性存储为2维张量。比如一个典型的邮件列表就很适用。
假设我们有10000个人,并且每个人又具有这些属性:
- 姓
- 名
- 街道
- 市
- 省
- 国家
- 邮编
张量是有“形状”的,“形状”适合数据维度且定义了张量最大尺寸,我们可以把人物属性放入一
个形状为(10000, 7)的2维张量当中。
你可能想说这个张量有10000列和7行。
やめて。
张量的行与列之间是可以相互转换的(所以不存在具体的“行”与“列”的定义)。
3维张量
其实到了3维,才是“张量”这个概念真正凸显的时候。我们经常需要把2维张量再装进另一个筐里,这就是3维张量。
在Numpy中,可以这样表示:
以上面的邮件列表为例。假设现在有10个邮件列表,我们可以把2维张量存至另一个筐,构成3维张量。形状如下:
(number_of_mailing_lists, number_of_people, number_of_characteristics_per_person)
(10,10000,7)
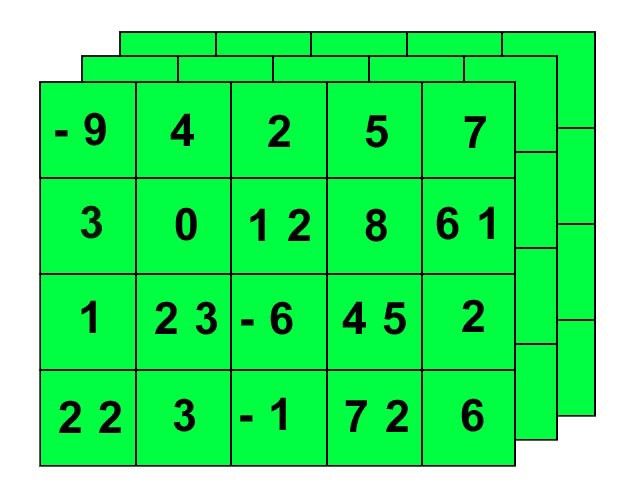
你可能已经猜到了, 3维张量是数字立方。
我们可以继续堆砌立方体来构建越来越大的张量,以表现4维,5维乃至N维的张量。
实际上3维张量可以更好地用层级网格来表示:
常见张量型数据
有几类常见的数据类型是以张量形式存储的:
- 3D = 时间序列
- 4D = 图像
- 5D = 视频
一条贯穿所有这些张量的线索就是“样本数量”。样本数量就是数据集里的数据个数,可以是图片的张数,视频的段数,文件的份数或是微博的条数。
一般实际的数据维数都会比样本数量小。
rest_of_dimensions - sample_size = actual_dimensions_of_data
考虑到不同维数下的形状(以不同的维度代表),我们要寻找能够描述数据的最少维度。
所以4维张量通常存储图像,因为样本数量就是张量的第4个维度。
比如一张图片可以用3个维度来表征:
(width, height, color_depth) = 3D
但在机器学习中,我们一般不是只跟单张图片或单份文件打交道,而是一个数据集。我们可能有10000张郁金香的照片,这就是一个4维张量:
(sample_size, width, height, color_depth) = 4D
下面来看几个不同维度张量的例子。
时序数据
3维张量对于时序数据很有效。
医学影像
我们可以把脑电波EEG信号编码为3维张量,因为它可以用3个参数指代:
(time, frequency, channel)
转换过程大致如下:
现在如果我们有很多病人扫描了脑电波,那就变成个4维张量了。
(sample_size, time, frequency, channel)
股价
股价每分钟都有高有低,有最终价。纽交所从上午9:30开到下午4:00,共计6个半小时,390分钟。 股价的变化一般用K线图表示:
我们可以把每分钟的高价,低价,最终价存为2维张量。如果抓取一星期(5个交易日),就是3维张量,形状如下:
(week_of_data, minutes, high_low_price)
(5,390,3)
如果有10支股票,则变成4维张量:
(10,5,390,3)
假设现在有个互惠基金,由若干支股票组成,以4维张量形式表征。我们可以持有25支互惠基金作为投资组合,于是就有一系列4维张量,等价于5维张量:
(25,10,5,390,3)
文本数据
文本数据也可以存为3维张量,以Twitter为例。
Tweets由140字组成,基于UTF-8标准,可以呈现上百万字,但实际上我们只对前128个感兴趣,与ASCII编码是一样的。单条tweet可以装载进一个(140,128)的2维矢量。
假如我们下载了100万条Trump的tweets(我觉得他一个礼拜就发够了。注:此条吐槽为原文),可以存为3维张量。
(number_of_tweets_captured, tweet, character)
(1000000,140,128)
图像
4维张量很适合存储一系列图像(如Jpeg格式)。如前所述,一张图片可以存为三个参数:
- 宽
- 高
- 色彩深度
单张图片是3维的,一系列图片就是4维的了,第4维就是sample_size。
著名的MNIST数据集就是一系列手写数字,曾经是困扰众多数据科学家的难题,今天已经基本上是玩儿透了,机器已经能够达到99%甚至更高的精度(单层CNN就差不多了)。 但是这个数据集仍然发挥着余热,就是用作新机器学习应用的样板,或者练手的素材。
Keras甚至集成了MNIST数据集,只需要简单的命令就可以导入。
from keras.datasets import mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
数据集被分为两份:
- 训练集
- 测试集
每个图片都有一个标签,即该图的真实数字,比如3,7或是9,这些标签时人工手动添加的。
训练集用来教会神经网络,测试集则是神经网络学习后试图分类的目标。
MNIST都是灰度图像,也就是说可以编码为2维张量,但是所有图片还是依照惯例编码为3维张量,第三个轴代表色彩深度。
MNIST数据集中有60000张图片,每张长宽皆为28像素,色彩深度为1,即灰度图片。
TensorFlow是这样存储图片的(与Theano格式有所不同):
(sample_size, height, width, color_depth).
彩图
彩色照片有着不同的色彩深度,这取决于分辨率和编码格式。典型的JPG图像用RGB编码,所以色彩深度为3,分别代表红、绿、蓝。
这是我家猫Dove的照片,分辨率为750x750,这意味着我们会有个3维张量:
(750,750,3)
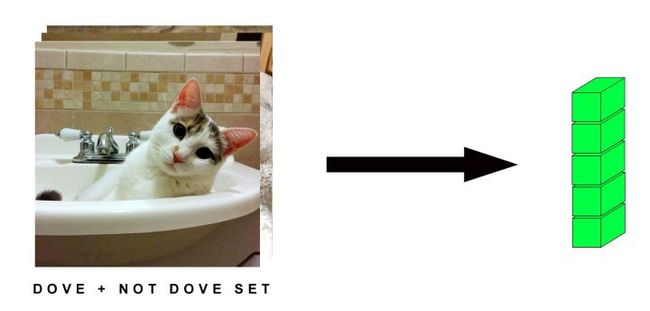
接下来我家Dove会被变成一系列冷冰冰的张量和公式,就像是在神经网络中“变形”,或是“流动”(Flow)。
假设我们有一堆各种猫的图片(尽管他们都没有Dove漂亮。注:原作者看来是个猫奴)。比如10000张别家猫的750x750照片。在Keras中,就这样定义为4维张量:
(10000,750,750,3)
5维张量
5维张量可以存视频数据。在TensorFlow中视频数据的编码形式如下:
sample_size, frames, width, height, color_depth)
一个5分钟的视频(300秒),1080p高清(1920x1080像素),每秒15个关键帧,色彩深度3,这是一个4维张量:
(4500,1920,1080,3)
张量的第五个维度是视频集中的视频个数。所以如果有10个视频,就有5维张量:
(10,4500,1920,1080,3)
这个例子其实很疯狂。
张量的体积可以大的不可思议, 超过1TB。在现实世界中,我们想要尽可能地下采样视频,否则模型可能永远都训练不完。
5维张量的值的个数为:
10 x 4500 x 1920 x 1080 x 3 = 279,936,000,000
Keras允许使用32位或64位的浮点数(dtype):
float32
float64
每个值都是一个32位的数字,这就意味着我们要把值的个数再乘32,转换为比特数,再转换为TB:
279,936,000,000 x 32 = 8,957,952,000,000
我不觉得这适用于32位系统(我会再找人算算),所以还是需要下采样。
实际上我用这个疯狂的例子,是为了引出预处理和数据缩减。
你不能直接就把原始数据扔进AI模型中,你需要整理、压缩数据使其更易于处理。
降低分辨率、删减冗余数据、限制帧数等,这也是数据科学家的任务之一。
如果你不能把数据玩儿坏,那么你也不能把它玩儿好。
结语
现在你应该对张量及相关的数据类型有了更好的理解。
再下一篇中,我们将学习如何用数学方法对张量进行变形。
换言之,我们要让Tensor "flow" 起来。