Delta机器人:运动学正反解分析
Delta机器人:运动学正反解分析
一、Delta机构简介
Delta机构是并联机构中的一种典型机构,起原始结构如图1所示。Delta机构由R.Clavel 博士在 1985年发明,是现在并联机器人中使用最多的一种,具备了并联机构所特有的优点,负载能力强、效率高、末端执行器精度高、运动惯性小,可以高速稳定运动等。因此在机器人领域获得了越来越广泛的应用。以实现高速、精准、高效的运动。
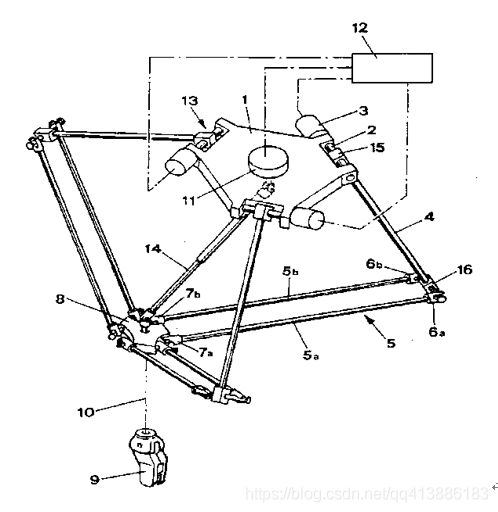
图 1 R . C l a v e l 博 士 发 明 的 D e l t a 机 构 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 图1\ R.Clavel 博士发明的Delta机构 图1 R.Clavel博士发明的Delta机构
二、数学模型建立
建立Delta机构简化数学模型如图2所示,其中圆 O Ο O所在平面为定平台,圆 p p p所在平面为动平台, ∆ C 1 C 2 C 3 ∆C_1C_2C_3 ∆C1C2C3和 ∆ A 1 A 2 A 3 ∆A_1A_2A_3 ∆A1A2A3为等边三角形,点 C 1 、 C 2 、 C 3 、 A 1 、 A 2 、 A 3 C_1、C_2、C_3、A_1、A_2、A_3 C1、C2、C3、A1、A2、A3分别为三个主动臂和三个从动臂与上下两个平台的连接点。
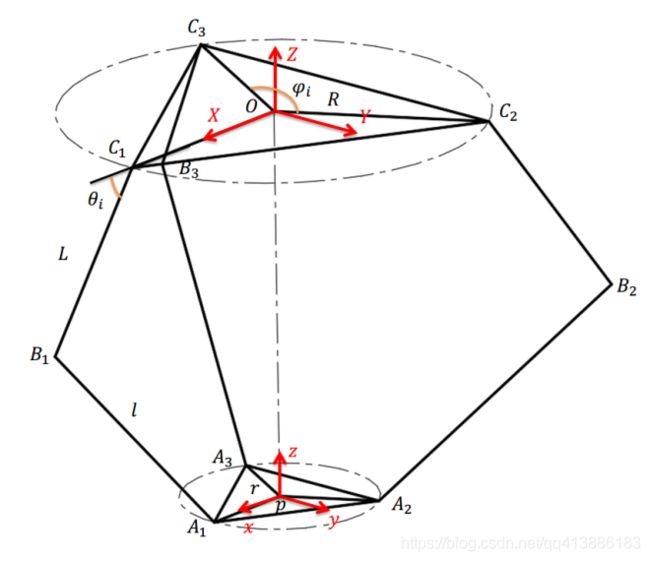
图 2 D e l t a 机 构 简 化 数 学 模 型 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 图2\ Delta机构简化数学模型 图2 Delta机构简化数学模型
如图2所示,以定平台中心 O Ο O建立坐标系 O − X Y Z Ο-XYZ O−XYZ,以动平台中心 p p p建立坐标系 p − x y z p-xyz p−xyz。由Delta机构的设计原理可知,三条支链完全对称,因此不妨设第 i ( i = 1 , 2 , 3 ) i(i=1,2,3) i(i=1,2,3)条支链的主动臂 ∣ B i C i ∣ \left|B_iC_i\right| ∣BiCi∣长度为 L L L,从动臂 ∣ A i B i ∣ \left|A_iB_i\right| ∣AiBi∣长度为 l l l,主动臂与定平台夹角为 θ i \theta_i θi,三条支链与X轴的夹角为 φ i = ( 2 ( i − 1 ) π / 3 ) , i = 1 , 2 , 3 , \varphi_i=\left(2\left(i-1\right)\pi/3\right),i=1,2,3, φi=(2(i−1)π/3),i=1,2,3,定平台半径为R,动平台半径为 r r r。
三、运动学正解
Delta机构的正解,是在已知三个主动臂转角的情况下求出动平台中心点 p p p在定平台所在坐标系中的坐标。Delta机构运动学正解的求法有很多种,此处采取几何解法,将 A i B i A_iB_i AiBi分别沿 A i p A_ip Aip平移使其交于点 p p p得到 D i p D_ip Dip,连接 D 1 D 2 D_1D_2 D1D2、 D 2 D 3 D_2D_3 D2D3、 D 3 D 1 D_3D_1 D3D1得到四棱锥 p − D 1 D 2 D 3 p{-D}_1D_2D_3 p−D1D2D3,如图3所示。
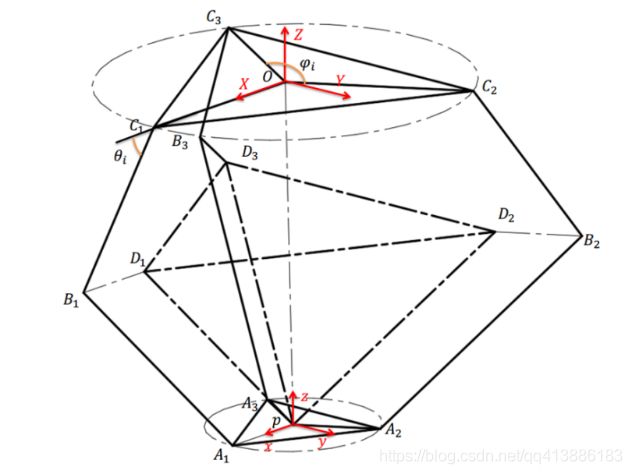
图 3 D e l t a 机 构 几 何 法 正 解 简 化 模 型 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 图3\ Delta机构几何法正解简化模型 图3 Delta机构几何法正解简化模型
根据上图不难得到,定平台三个铰接点 C 1 、 C 2 、 C 3 C_1、C_2、C_3 C1、C2、C3的坐标为
[ x i y i z i ] = [ R cos φ i R sin φ i 0 ] , i = 1 , 2 , 3 ( 1 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left[\begin{matrix}x_i\\y_i\\z_i\\\end{matrix}\right]=\left[\begin{matrix}R\cos{\varphi_i}\\R\sin{\varphi_i}\\0\\\end{matrix}\right],i=1,2,3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) ⎣⎡xiyizi⎦⎤=⎣⎡RcosφiRsinφi0⎦⎤,i=1,2,3 (1)
向量 O B i ⃗ \vec{OB_i} OBi可表示为
O B i ⃗ = O C i ⃗ + C i B i ⃗ , i = 1 , 2 , 3 ( 2 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vec{\ OB_i}=\vec{OC_i}+\vec{C_iB_i},i=1,2,3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) OBi=OCi+CiBi,i=1,2,3 (2)
其中 C i B i ⃗ \vec{C_iB_i} CiBi又可表示为
[ x i y i z i ] = [ − L sin θ i cos φ i − L sin θ i sin φ i − L cos θ i ] , i = 1 , 2 , 3 ( 3 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left[\begin{matrix}x_i\\y_i\\z_i\\\end{matrix}\right]=\left[\begin{matrix}-L\sin{\theta_i}\cos{\varphi_i}-L\sin{\theta_i}\sin{\varphi_i}\\-L\cos{\theta_i}\\\end{matrix}\right],i=1,2,3\ \ \ \ \ \ (3) ⎣⎡xiyizi⎦⎤=[−Lsinθicosφi−Lsinθisinφi−Lcosθi],i=1,2,3 (3)
又 A i p ⃗ \vec{A_ip} Aip可表示为
[ x i y i z i ] = [ − r cos φ i − r sin φ i 0 ] , i = 1 , 2 , 3 ( 4 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left[\begin{matrix}x_i\\y_i\\z_i\\\end{matrix}\right]=\left[\begin{matrix}-r\cos{\varphi_i}\\-r\sin{\varphi_i}\\0\\\end{matrix}\right],i=1,2,3\ \ \ \ \ \ \ \ \ \ \ (4) ⎣⎡xiyizi⎦⎤=⎣⎡−rcosφi−rsinφi0⎦⎤,i=1,2,3 (4)
则 O D i ⃗ \vec{OD_i} ODi可以表示为
O D i ⃗ = O B i ⃗ + B i D i ⃗ ( 5 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vec{OD_i}=\vec{\ OB_i}+\vec{\ B_iD_i}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) ODi= OBi+ BiDi (5)
其中由Delta机构的几何性质可知
B i D i ⃗ = A i p ⃗ ( 6 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vec{\ B_iD_i}=\vec{A_ip}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) BiDi=Aip (6)
所以
O D i ⃗ = O C i ⃗ + C i B i ⃗ + A i p ⃗ ( 7 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vec{OD_i}=\vec{OC_i}+\vec{C_iB_i}+\vec{A_ip}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (7) ODi=OCi+CiBi+Aip (7)
综合式(1)—(7)可得,在坐标系Ο-XYZ中D_i的坐标为
[ x i y i z i ] = [ ( R − r − L sin θ i ) cos φ i ( R − r − L sin θ i ) sin φ i − L cos θ i ] , i = 1 , 2 , 3 ( 8 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left[\begin{matrix}x_i\\y_i\\z_i\\\end{matrix}\right]=\left[\begin{matrix}\left(R-r-L\sin{\theta_i}\right)\cos{\varphi_i}\\\left(R-r-L\sin{\theta_i}\right)\sin{\varphi_i}\\-L\cos{\theta_i}\\\end{matrix}\right],i=1,2,3\ \ \ \ \ \ \ \ \ (8) ⎣⎡xiyizi⎦⎤=⎣⎡(R−r−Lsinθi)cosφi(R−r−Lsinθi)sinφi−Lcosθi⎦⎤,i=1,2,3 (8)
此时不难发现,Delta机构的正运动学解算已经转化为已知三个顶点坐标和各棱的长度求解另外一个顶点坐标的问题。将图2.4中的四棱锥 p − D 1 D 2 D 3 p{-D}_1D_2D_3 p−D1D2D3取出单独分析,作垂线 p E pE pE垂直于平面 D 1 D 2 D 3 D_1D_2D_3 D1D2D3于点 E E E,取 D 2 D 3 D_2D_3 D2D3中点 F F F,连接 E F EF EF、 E D 2 ED_2 ED2,如图3所示。

图 4 等 效 四 棱 锥 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 图4\ 等效四棱锥 图4 等效四棱锥
不难证明,点E为三角形D_1D_2D_3的外接圆圆心。
则向量 O p ⃗ \vec{Op} Op可表示为
O p ⃗ = O E ⃗ + E p ⃗ ( 9 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vec{Op}=\vec{OE}+\vec{Ep}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) Op=OE+Ep (9)
O E ⃗ \vec{OE} OE可以表示为
O E ⃗ = O F ⃗ + F E ⃗ ( 10 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vec{OE}=\vec{OF}+\vec{FE}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (10) OE=OF+FE (10)
其中, O F ⃗ = ( O D 2 ⃗ + O D 3 ⃗ ) / 2 \vec{OF}=\left(\vec{OD_2}+\vec{OD_3}\right)/2 OF=(OD2+OD3)/2, F E ⃗ = ∣ F E ⃗ ∣ n F E ⃗ \vec{FE}=\left|\vec{FE}\right|\vec{n_{FE}} FE=∣∣∣FE∣∣∣nFE。
对于向量 F E ⃗ \vec{FE} FE其长度为
∣ F E ⃗ ∣ = ∣ D 2 E ∣ 2 − ∣ D 2 F ∣ 2 ( 11 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left|\vec{FE}\right|=\sqrt{\left|D_2E\right|^2-\left|D_2F\right|^2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (11) ∣∣∣FE∣∣∣=∣D2E∣2−∣D2F∣2 (11)
其中, ∣ D 2 E ∣ \left|D_2E\right| ∣D2E∣为三角形 D 1 D 2 D 3 D_1D_2D_3 D1D2D3的外接圆半径,可用公式(12)计算
∣ D 2 E ∣ = a b c 4 S ( 12 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left|D_2E\right|=\frac{abc}{4S}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(12\right) ∣D2E∣=4Sabc (12)
其中
S = p ( p − a ) ( p − b ) ( p − c ) ( 13 ) p = ( a + b + c ) 2 ( 14 ) S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\ \ \ \ \ \ \ \ \left(13\right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ p=\frac{\left(a+b+c\right)}{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (14) S=p(p−a)(p−b)(p−c) (13) p=2(a+b+c) (14)
a 、 b 、 c a、b、c a、b、c是三角形 D 1 D 2 D 3 D_1D_2D_3 D1D2D3的边长。
联立(11)—(14)可得
∣ F E ⃗ ∣ = ( a 2 + b 2 − c 2 ) c 8 S ( 15 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left|\vec{FE}\right|=\frac{\left(a^2+b^2-c^2\right)c}{8S}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (15) ∣∣∣FE∣∣∣=8S(a2+b2−c2)c (15)
向量 F E ⃗ \vec{FE} FE的单位方向向量为
n F E ⃗ = D 2 D 1 ⃗ × D 2 D 3 ⃗ × D 3 D 2 ⃗ ∣ D 2 D 1 ⃗ × D 2 D 3 ⃗ × D 3 D 2 ⃗ ∣ ( 16 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vec{n_{FE}}=\frac{\vec{D_2D_1}\times\vec{D_2D_3}\times\vec{D_3D_2}}{\left|\vec{D_2D_1}\times\vec{D_2D_3}\times\vec{D_3D_2}\right|}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (16) nFE=∣D2D1×D2D3×D3D2∣D2D1×D2D3×D3D2 (16)
又向量 E p ⃗ \vec{Ep} Ep的方向向量
n E p ⃗ = D 2 D 1 ⃗ × D 2 D 3 ⃗ ∣ D 2 D 1 ⃗ × D 2 D 3 ⃗ ∣ ( 17 ) \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vec{n_{Ep}}=\frac{\vec{D_2D_1}\times\vec{D_2D_3}}{\left|\vec{D_2D_1}\times\vec{D_2D_3}\right|}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (17) nEp=∣D2D1×D2D3∣D2D1×D2D3 (17)
长度为
E p ⃗ = ∣ D 1 p ⃗ ∣ 2 − ∣ D 1 E ⃗ ∣ 2 ( 18 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vec{Ep}=\sqrt{\left|\vec{D_1p}\right|^2-\left|\vec{D_1E}\right|^2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ (18) Ep=∣∣∣D1p∣∣∣2−∣∣∣D1E∣∣∣2 (18)
其中 ∣ D 1 p ⃗ ∣ = ∣ B 1 A 1 ⃗ ∣ = l , D 1 E ⃗ \left|\vec{D_1p}\right|=\left|\vec{B_1A_1}\right|=l,\vec{D_1E} ∣∣∣D1p∣∣∣=∣∣∣B1A1∣∣∣=l,D1E为外接圆半径。
将(10)—(18)式联立求解带入(9)式即可求得Delta机构正解。
四、运动学反解
运动学反解是在已知机器人 p p p点的位置 ( x , y , z ) (x,y,z) (x,y,z)的情况下求解三个主动臂需要转过的角度 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2、 θ 3 \theta_3 θ3,与串联机器人不同,并联机器人的反解较易求得,此处只需要根据杆长进行约束即可很容易解出,求解过程在文献[3]中有详细的说明,此处不再推导,仅根据图5所示的单支链求解示意图给出最终的求解结果。

图 5 单 支 链 求 解 示 意 图 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 图5\ 单支链求解示意图 图5 单支链求解示意图
θ i = 2 a r c t a n ( − B i − B i 2 − 4 A i C i 2 A i ) , i = 1 , 2 , 3 ( 19 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \theta_i=2arctan\left(\frac{-B_i-\sqrt{B_i^2-4A_iC_i}}{2A_i}\right),i=1,2,3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (19) θi=2arctan(2Ai−Bi−Bi2−4AiCi),i=1,2,3 (19)
其中
A 1 = x 2 + y 2 + z 2 + R − r 2 + L 2 − l 2 − 2 x ( R − r ) 2 L − ( R − r − x ) A1=x2+y2+z2+R-r2+L2-l2-2x(R-r)2L-(R-r-x) A1=x2+y2+z2+R−r2+L2−l2−2x(R−r)2L−(R−r−x)
B 1 = 2 z B1=2z B1=2z
C 1 = x 2 + y 2 + z 2 + R − r 2 + L 2 − l 2 − 2 x ( R − r ) 2 L + ( R − r − x ) C1=x2+y2+z2+R-r2+L2-l2-2x(R-r)2L+(R-r-x) C1=x2+y2+z2+R−r2+L2−l2−2x(R−r)2L+(R−r−x)
A 2 = x 2 + y 2 + z 2 + R − r 2 + L 2 − l 2 + ( x − 3 y ) ( R − r ) L − 2 R − r − ( x − 3 y ) A2=x2+y2+z2+R-r2+L2-l2+(x-3y)(R-r)L-2R-r-(x-3y) A2=x2+y2+z2+R−r2+L2−l2+(x−3y)(R−r)L−2R−r−(x−3y)
B 2 = 4 z B2=4z B2=4z
C 2 = x 2 + y 2 + z 2 + R − r 2 + L 2 − l 2 + ( x − 3 y ) ( R − r ) L + 2 R − r + ( x − 3 y ) C2=x2+y2+z2+R-r2+L2-l2+(x-3y)(R-r)L+2R-r+(x-3y) C2=x2+y2+z2+R−r2+L2−l2+(x−3y)(R−r)L+2R−r+(x−3y)
A 3 = x 2 + y 2 + z 2 + R − r 2 + L 2 − l 2 + ( x + 3 y ) ( R − r ) L − 2 R − r − ( x + 3 y ) A3=x2+y2+z2+R-r2+L2-l2+(x+3y)(R-r)L-2R-r-(x+3y) A3=x2+y2+z2+R−r2+L2−l2+(x+3y)(R−r)L−2R−r−(x+3y)
B 3 = 4 z B3=4z B3=4z
C 3 = x 2 + y 2 + z 2 + R − r 2 + L 2 − l 2 + ( x + 3 y ) ( R − r ) L + 2 R − r + ( x + 3 y ) C3=x2+y2+z2+R-r2+L2-l2+(x+3y)(R-r)L+2R-r+(x+3y) C3=x2+y2+z2+R−r2+L2−l2+(x+3y)(R−r)L+2R−r+(x+3y)
至此,Delta机构的运动学正反解均以求解完毕。
五、参考文献
[1] Clavel R. Dispositif pour le deplacement et le positionnement d’un element dans l’espace[P].Switzerland: CH1985005348856,1985.
[2] 赵杰,朱延河,蔡鹤皋.Delta型并联机器人运动学正解几何解法[J].哈尔滨工业大学学报,2003(01):25-27.
[3] 伍经纹,徐世许,王鹏,宋婷婷.基于Adams的三自由度Delta机械手的运动学仿真分析[J].软件,2017,38(06):108-112.