高数 高斯公式、泰勒公式、麦克劳伦公式、欧拉公式、傅里叶公式

 一、高斯公式
一、高斯公式
参考文章:图像处理 高斯滤波(带权值的均值滤波)
1、一维高斯滤波。
a表示得到曲线的高度,u是指曲线在x轴的中心, σ指width(与半峰全宽有关,即平方差)。
2、二维高斯滤波。
二、泰勒公式
1、泰勒公式介绍。
设n是一个正整数。如果定义在一个包含aa的区间上的函数f在a点处n+1次可导,那么对于这个区间上的任意x都可以用泰勒公式来表示。如果函数足够平滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还给出了这个多项式和实际的函数值之间的偏差。
2、拉格朗日中值定理。
曲线在A,B间至少存在1点,使得该曲线在P点的切线与割线AB平行。对于曲线运动在任意一个运动过程中至少存在一个位置或一个时刻的瞬时速率等于这个过程中的平均速率。如果函数f(x)满足,在[a,b]上连续,在(a,b)上可导,那么至少有一点θ(a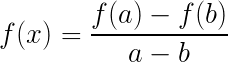 成立。
成立。
三、麦克劳伦公式
1、麦克劳伦公式介绍。
泰勒公式中当a=0的时候,就是麦克劳伦公式。
2、例子。
1)、![]() :
:
因为![]() 的导数还是
的导数还是 ![]() ,而且
,而且![]() 。
。
2)、sinx:
因为sin0 = 0。
sin'x = cosx,sin'0 = cos0 = 1。
sin''x = cos'x = -sinx,sin''0 = -sin0 = 0。
sin'''x = cos''x = -sin'x=-cosx,sin'''0 = -cos0 = -1。
sin''''x = cos'''x = -sin''x = -cos'x = sinx,sin'''0 = sin0 = 0。
3)、cosx:
因为cos0=1
cos'x=-sinx,cos'0=sin0=0。
cos''x=-sin'x=-cosx,cos''0=-cos0=-1。
cos'''x=-sin''x=-cos'x=sinx,cos'''0=sin0=0。
cos''''x=-sin'''x=-cos''x=sin'x=cosx,cos''''0=cos0=1。
四、欧拉公式
因为:
所以:
,
五、傅里叶公式
参考文章:一维离散傅里叶变换、二维离散傅里叶变换、一维快速傅里叶变换、二维离散傅里叶变换(代码和性能的优化)
1、傅里叶变换。
傅立叶变换,也可以看作是泰勒公式的一种。表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。时域和频域有关联:连续对非周期,离散对周期。
| 原始信号 | 傅里叶方法 | 时域 | 频域 |
| 非周期性连续信号 | (连续)傅立叶变换(FT) | 连续、非周期 | 连续、非周期 |
| 周期性连续信号 | 傅立叶级数(FS) | 连续、周期 | 离散、非周期 |
| 非周期性离散信号 | 离散时域傅立叶变换(DTFT) | 离散、非周期 | 连续、周期 |
| 周期性离散信号 | 离散傅立叶变换(DFT) | 离散、周期 | 离散、周期 |
2、一维离散傅里叶变换DFT。
一维DFT公式中的 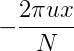 就是欧拉公式中的x,而且cos(-x)=cosx,sin(-x)=-sinx。
就是欧拉公式中的x,而且cos(-x)=cosx,sin(-x)=-sinx。
3、一维离散傅里叶逆变换IDFT。
4、二维离散傅里叶变换DFT。
5、二维离散傅里叶逆变换IDFT。
6、一维傅里叶快速变换FFT。
1)FFT(Fast Fourier Transformation)是离散傅氏变换(DFT)的快速算法,即利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少,特别是被变换的抽样点数N越多,FFT算法计算量的节省就越显著。即为快速傅氏变换。它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。
2)因为根据欧拉公式![]() 和一维离散傅里叶公式,可以将欧拉公式中的
和一维离散傅里叶公式,可以将欧拉公式中的![]() 看作是
看作是![]() ,而且可以是要将其代入到cos和sin函数中,所以其实可以看作是一个半径为1的圆。而
,而且可以是要将其代入到cos和sin函数中,所以其实可以看作是一个半径为1的圆。而![]() 可以看作将圆分成N份,即上面那个矩阵中的
可以看作将圆分成N份,即上面那个矩阵中的![]() ,而第k份的那个点就是那个值。
,而第k份的那个点就是那个值。
3)可以推导出关系。
周期性:![]() ,
, ![]()
原点对称:![]()
4)要让DFT的长度等于2的n次幂,其中n是正整数。
令 ![]() ,
,![]() ,
,
则![]() 。
。
但是这里的k是小于![]() 的,但是可以推导出
的,但是可以推导出![]() , 其中
, 其中![]() 。
。
5)最后将G(x),P(x)按照这个方式,用分治法不停的拆分出来,剩下最后俩个 ,然后返回计算的结果。
7、一维逆傅里叶快速变换IFFT。
比较DFT和IDFT公式,会发现逆变换和正变换的区别在于:
1、![]() 中的
中的![]() 正负的区别。
正负的区别。
2、逆变换在结束之后,每个值都要除以原数组的大小。
所以我们只要套用FFT的算法就可以了,将F(k)作为输入数组,输出f(x)作为输出数组,将因子![]() 改为
改为![]() ,最后将f(x)全部除以N就可以了。
,最后将f(x)全部除以N就可以了。

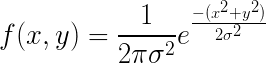



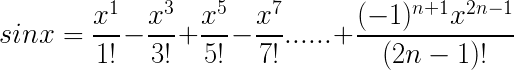

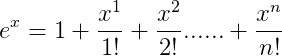

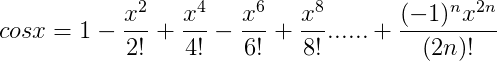
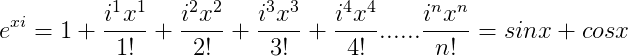
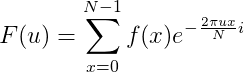
![F(u)=\sum_{x=0}^{N-1}f(x)[cos \frac{2\pi ux}{N}-sin \frac{2\pi ux}{N}i]](http://img.e-com-net.com/image/info8/fcb36dbab4144a53aca57323b19f6ca8.gif)
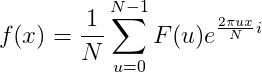
![f(x)=\frac{1}{N}\sum_{u=0}^{N-1}F(u)[cos \frac{2\pi ux}{N}+sin \frac{2\pi ux}{N}i]](http://img.e-com-net.com/image/info8/cf492d8fbf8341db9585cea8355d6caa.gif)

![F(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)[cos(2\pi (\frac{ux}{M}+\frac{vy}{N})) -sin(2\pi (\frac{ux}{M}+\frac{vy}{N}))i ]](http://img.e-com-net.com/image/info8/85949d9bf0d841ddaec0e326c90ad7a5.gif)
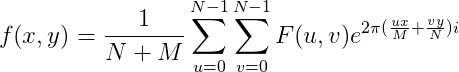
![F(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)[cos(2\pi (\frac{ux}{M}+\frac{vy}{N}))+sin(2\pi (\frac{ux}{M}+\frac{vy}{N}))i ]](http://img.e-com-net.com/image/info8/88d90688f5424577ba02cfd4487b9b34.gif)
