LightGBM详解--原理+技巧+参数

  尽管XGBoost和pGBRT等对GBDT有所改善，但是LightGBM认为在数据量大、特征多的时候，XGBoost和pGBRT等的有效性和可拓展性仍然不被满足。一个最主要的原因是对于每一个特征，都需要遍历所有的数据样例，来估计所有可能分裂点的信息增益（这里叫增益比较恰当），正因如此，非常耗时。
  
  故LightGBM提出了两个改进思路，GOSS（Gradient-based One-Side Sampling，基于梯度的单边采样）和EFB（Exclusive Feature Bundling，互斥特征捆绑）。
     GOSS： 每个样本在计算信息增益过程中，有不同的梯度，由信息增益的定义可知，梯度大的样本会贡献较大的梯度。因此排除很大比例的梯度小的数据样例，用剩下的数据样本估计信息增益，证明梯度大的样本更重要。
     EFB：捆绑互斥的特征来减少特征数，尽管这是个NP问题，但一个贪心算法仍然能获得一个好的近似分数。因此，可以在不损失准确率的前提下，降低特征的个数。
  LightGBM可以认为是GBDT加入了GOSS和EFB的改善。在大量公开数据集的实验表明，LightGBM比GBDT快20多倍，并且准确率相当。
  
  GBDT+pre-sorted：通过忽略特征中的零值（稀疏性导致），来降低训练成本；
  GBDT+Histogram-based：无有效的稀疏优化方法，因为无论特征是否为0，都需要找到条件的箱值。
  

LightGBM原理

GOSS

  AdaBoost中每个样本有权重，但是GBDT中每个样本没有权重，因此AdaBoost中的抽样方法不能直接在GBDT中应用。但是GBDT的每个样本含有的梯度对数据抽样具有有用的信息。样本的梯度小，那么它的训练误差就小，总是训练的很好。一个直接的方法就是丢弃这些梯度小的样本，但是会导致数据分布变化，会损坏学习器的精度。为了避免这个问题，提出GOSS。
  正如上所述，GOSS为了避免数据分布改变的问题，其目的是选择梯度大的样本，对于梯度小的样本，采用下采样的方式，但在下采样过程中，仅仅随机地排除梯度小的样本，而仅仅随机排除，达到的效果比随机均匀下采样更好（疑问，梯度大小的判断标准是什么？）。
  GOSS先根据所有样本的梯度绝对值进行排序，选取前$a\ast 100\%$个样本（称为集合$A$），在剩下的$(1-a)\ast 100\%$个样本（称为集合$A^c$）中，随机抽取$b\ast 100\%$个样本（称为集合$B$，$B$的大小为$b\ast |A^c|$）（则一共随机选取的梯度小的样本占比$b\ast (1-a)\ast 100\%$）生成一个小梯度样本集。在小梯度样本计算信息增益时，乘以一个常数系数$\frac{1-a}{b}$。这样，只需要更多的关注训练不足的样本，而没有较多的改变原始数据分布。
  
  GBDT的分裂准则：令$O$为决策树的一个分裂节点上的训练数据，在这个分裂节点上，特征$j$在点$d$上分裂的方差增益为：
$$V_{j|O}(d)=\frac{1}{n_O}\left(\frac{{\left({\sum }_{\left\{x_i\in O:x_{ij}\le d\right\}}{g}_i\right)}^2}{n_{l|O}^j(d)}+\frac{{\left({\sum }_{\left\{x_i\in O:x_{ij}>d\right\}}{g}_i\right)}^2}{n_{r|O}^j(d)}\right)$$$$\text{ where }{n}_O=\sum I\left[x_i\in O\right],n_{l|O}^j(d)=\sum I\left[x_i\in O:x_{ij}\le d\right]\text{ and }{n}_{r|O}^j(d)=\sum I\left[x_i\in O:x_{ij}>d\right]$$
  对于特征$j$，决策树算法选择最优的分裂点$d_j^{\ast }=argma{x}_d{V}_j(d)$，然后计算最大的增益$V_j(d_j^{\ast })$，然后根据特征$j^{\ast }$在点$d_{j^{\ast }}$处将数据分裂为左右子节点。
  对于GOSS，在$A\cup B$集合上，通过估计方差增益${\tilde{V}}_j(d)$来划分数据，$${\tilde{V}}_j(d)=\frac{1}{n}\left(\frac{{\left({\sum }_{x_i\in A_i}{g}_i+\frac{1-\alpha }{b}{\sum }_{x_i\in B_l}{g}_i\right)}^2}{n_i^j(d)}+\frac{{\left({\sum }_{x_i\in A_r}{g}_i+\frac{1-a}{b}{\sum }_{x_i\in B_r}{g}_i\right)}^2}{n_r^j(d)}\right)$$$$\text{ where }{A}_l=\{x_i\in A：x_{ij}\le d\},A_r=\{x_i\in A:x_{ij}>d\},B_l=\{x_i\in B：x_{ij}\le d\},B_r=\{x_i\in B：x_{ij}>d\}$$
  同时$\frac{1-a}{b}$被用来归一化数据集$B$的梯度之和。
  因此，通过GOSS，我们只需要在较小数据集上计算${\tilde{V}}_j(d)$来决定分裂点即可，而不需要在完整数据集计算。这样做的优点是（1）大幅降低计算成本；（2）不会损失多少训练准确性；（3）比随机抽样本表现更好。

  令$\epsilon (d)=|{\tilde{V}}_j(d)-V_j(d)|$作为GOSS的近似误差，${\bar{g}}_l^j(d)=\frac{{\sum }_{x_i\in {\left(A\cup A^c\right)}_l}|g_i|}{n_l^j(d)}$，${\bar{g}}_r^j(d)=\frac{{\sum }_{x_i\in {\left(A\cup A^c\right)}_r}|g_i|}{n_r^j(d)}$，则$$\mathcal{E}(d)\le C_{a,b}^2\ln 1/\delta \cdot \max \left\{\frac{1}{n_l^j(d)},\frac{1}{n_r^j(d)}\right\}+2D{C}_{a,b}\sqrt{\frac{\ln 1/\delta }{n}},(1)$$$$\text{ where }{C}_{a,b}=\frac{1-a}{\sqrt{b}}\underset{x_i\in A^c}{\max }\left|g_i\right|,\text{ and }D=\max \left({\bar{g}}_l^j(d),{\bar{g}}_r^j(d)\right)$$
  基于此，有如下结论：（1）GOSS的渐近近似几率为$O(\frac{1}{n_l^j(d)}+\frac{1}{n_r^j(d)}+\frac{1}{\surd n})$，如果分裂不平衡（例如$n_l^j(d)\ge O(\surd n)$或者$n_r^j(d)\ge O(\surd n)$），则近似几率取决于式（1）的第二项（当n->∞，第二项趋向于0），这意味着当样本数量很大时，近似几率相当准确。（2）当$a=0$时，GOSS退化为随机采样算法，当$a=1$时，GOSS算法变为采取整个样本的算法。

  GOSS的泛化性能。令泛化误差为${\epsilon }_{gen}^{GOSS}(d)=|{\tilde{V}}_j(d)-V_{\ast }(d)|$（为抽样的训练样本方差增益与真实的方差增益之差）$\le |{\tilde{V}}_j(d)-V_j(d)|+|V_j(d)-V_{\ast }(d)|\triangleq {\epsilon }_{GOSS}(d)+{\epsilon }_{gen}(d)$，则采样可提高基学习器的多样性（潜在改善泛化表现）。

  以上说的是GOSS的样本采样的方式（不同于平常的随机抽样）。下面阐述EFB的特征采样方式（不同于一般的特征抽样方法）。

EFB

  实际应用过程中，尽管有大量的特征，但是很多特征都是相当稀疏的，这提供了一个几乎无损的方法来减少有效特征的数量的可能性。将互斥的特征捆绑为一个特征，设计一个有效的算法，将优化捆绑问题作为图着色问题，使用贪心算法，近似求解。对特征捆绑，可将复杂度从$O(data\ast feature)$降到$O(data\ast bundle)$，其中$bundle$远远小于$feature$，这就是加速的原因。
  这涉及两个问题，（1）如何确定哪些特征应该被捆绑？（2）如何去构造这些捆绑？
  对于第一个问题，是一个$NP-hard$，即在多项式时间内，无法找到一个精确方式。因此找到一个近似算法。$a$、将最优的捆绑问题转化为图着色问题（特征为点，如果任何两个特征之间不互斥，则添加边）；$b$、用贪心的算法可产生合理的捆绑（一个常数逼近比率）；$c$、因为有少部分特征，不是$100\%$互斥，若允许小的冲突，可以得到更小度量的特征绑定和提高计算效率（选择合适小的冲突比率，能平衡准确率和效率）。
  贪心算法：（1）构建带权重的边，该权重依赖于所以特征之间的总冲突；（2）根据特征度降序排序特征；（3）检查每个特征（排序列表中的），然后指派特征到一个存在的捆绑（包含小的冲突）或创建一个新的捆绑。其时间复杂度为$O(featur{e}^2)$。特征数多时，时间复杂度较高，仍然不可接受，故可提出一个更高效的无图有序策略以进一步提升效率，依靠非零值的数量排序（和度排序非常相似），非零值呢个导致更高概率的冲突。
  对于第二个问题，为了降低训练复杂度，需要在同一个捆绑中，将特征进行整合。关键是确保原始特征能从特征捆绑中区分出来。由于基于直方图的算法将特征值以离散箱的形式存储而不是连续值存储，因此可以利用不同箱中的排他特征来构建特征捆绑。通过增加偏移估计，可以实现的这样的特征捆绑，达到减少特征的目的。
  EFB可以捆绑很多互斥特征至更稀疏的特征，对于零值特征可以避免不必要的计算。通过用表标记非零值来直接忽视零值特征以优化基础的直方图算法，可使直方图构建成本从$O(data)$降至$O(non\_zero\_data)$，但值得注意的是，在整个树的生长过程中，用表标记的方法需要额外的内存和计算成本。

直方图算法

  LIghtGBM选择了基于Histogram的决策树算法，相比于XGBoost采用预排序处理分裂节点，LightGBM的Histogram算法在内存消耗和计算代价上都有很多优势。
  直方图算法的原理：对于连续特征，先将连续的浮点特征值离散化为k整数，同时构造成一个宽度为k的直方图（bins）；对于分类特征，每一种取值放入一个bin，且当取值的个数大于max bin数时，忽略那些很少出现的category值。在遍历数据的时候，根据离散化后的值作为索引，在直方图中累积统计量，然后根据直方图的离散值，遍历寻找最优的分割点（在XGBoost中需要遍历所有离散化的值，而LightGBM通过建立直方图只需要遍历k个直方图的值）。
  因此，在节点分裂的时候，不需要按照预排序算法那样对每个特征计算#data遍，仅需要计算#bins遍，大大加快了训练速度。
  直方图优化算法需要在训练前预先将特征值转化为bin value，也就是对每个特征的取值做个分段函数，将所有样本在该特征上划分到某一段（bin）中，最终把特征值从连续值转化成了离散值。值得注意的是，特征值对应的bin value在整个训练过程中是不会改变的。
  直方图优化算法过程：
  （1）对每个特征，为其创建一个直方图，这个直方图存储两类信息，分别是每个bin中样本的梯度之和，以及每个bin中样本数量。
  （2）对于每个特征，遍历所有的样本，累积上述的两类统计值到样本所属的bin中，即直方图的每个bin中包含了一定的样本，在此计算每个bin中的样本梯度之和并对bin中的样本计数。
  （3）对于某个叶节点，遍历所有的bin，分别以当前bin作为分割点，累加其左边的bin至当前bin的梯度和以及样本数量，并与父节点上的总梯度和以及总样本数量相减，得到右边所有bin的梯度和以及样本数量，并以此计算增益，在遍历过程中，取最大的增益，以此时的特征和bin的特征值作为分裂节点的特征和分裂特征取值。
  （4）对所有的叶节点，重复上述操作，遍历所有的特征，找到增益最大的特征及其划分值，以此来分裂该叶节点。
  从以上分析可知，有如下两个问题：

问题一：如何将特征值映射到bin中？

  由于LightGBM可以处理类别特征，因此对连续特征和类别特征的处理方式是不一样的。
  （1）对于连续特征，可以得到数值型特征取值（负数，0，正数）的各个bin的切分点。
  （2）对于离散特征（LightGBM支持类别特征，采用many vs many方式，不需要做One-Hot编码），先对特征取值出现的次数排序（从大到小），忽略一些出现次数很少的特征取值，为每一个特征值建立一个bin容器，对于在bin容器内出现次数较少的特征值直接过滤掉，不建立bin容器。

问题二：如何构建直方图

  对于离散特征或者连续特征，每一个划分阈值对应着一个bin容器编号，根据不同的bin容器，构建直方图，累加一阶和二阶梯度还有count。
  

直方图作差加速

  对于Histogram算法，有一个技巧就是直方图作差加速：一个叶节点的直方图（梯度之和以及样本数量）可以由它的父节点的直方图与它兄弟的直方图作差得到。利用这个方法，LightGBM可以在构造一个叶节点（含有较少数据）的直方图后，可使用非常微小的代价就可以得到它兄弟叶节点（含有较多数据）的直方图。
  因为构建兄弟叶节点的直方图是作差得到的，时间复杂度仅为$O(bins)$，几乎可以忽略，比起不作差得到的兄弟节点的直方图，速可以提升一倍。

leaf-wise分裂策略

  level-wise（XGBoost的）是指对每一层所有的节点做无差别分裂，尽管部分节点的增益比较小，依然会进行分裂，带来了不必要的开销（值得注意的是它容易多线程优化，方便控制模型复杂度，不容易过拟合）。

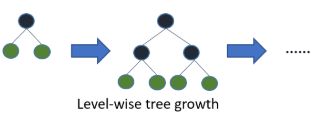
  leaf-wise（LightGBM的）是指在当前所有叶节点中选择分类增益最大的节点进行分裂，并进行最大深度限制，避免过拟合。

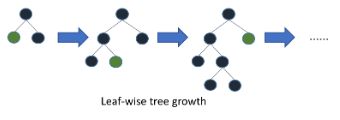
  在分裂次数相同的情况下，leaf-wise可以降低更多的误差，得到更好的精度。但leaf-wise的缺点是可能会长出比较深的决策树，容易过拟合，因此在leaf-wise之上增加了一个最大深度的限制，在保证高效的同时防止过拟合。

LightGBM加速的原因

  LightGBM的加速主要来自于GOSS+EFB，以及并行处理，并且不会损失准确率。
  GOSS加速的原因：根据梯度抽样，用抽样后的数据训练树。但速度并未如抽样比例那样，因为抽样之前要对全样本进行梯度计算，并对全样本进行预测。值得注意的是，GOSS抽样方式优于随机抽样。
  EFB加速的原因：合并许多稀疏特征（包括One-Hot和隐式排他特征）为更少的特征（在捆绑过程中），基于直方图算法，其也改善了内存（许多先验的孤立特征被捆绑在一起）。
  高效并行加速：（1）特征并行，在不同的机器上的不同特征集上分别寻找最优的分割点，在机器间同步最优的分割点，其通过本地保存全部数据避免对数据切分结果的通信；（2）数据并行：不同的机器先在本地构造直方图，然后进行全局合并，最后在合并的直方图上寻找最优分割点，其使用分散规约（Reduce scatter）把直方图合并的任务分摊到不同的机器上，并利用直方图作差，降低了通信量，减少了通信时间。
  LightGBM的GOSS和EFB改进能处理大量数据和大量特征，能显著提高算力和降低内存消耗。

LightGBM的优劣点

优点

  1、由于使用基于直方图算法，效率高、内存使用低（内存消耗仅是预排序算法的1/8）；
  2、用直方图算法的数据并行时，数据间通信代价低（值得注意的是，XGBoost也使用直方图来降低通信代价）；
  3、计算上的优势是大幅减少了计算分割点增益的次数。对每个特征，预排序需要对每一个不同的特征值都计算一次分割增益，而直方图算法只需要计算#bins次；
  4、cache-miss。预排序中，对梯度的访问以及对于索引表的访问，造成严重的cache-miss问题。但直方图算法，在计算增益的时候，只需要对bin进行访问，造成的cache-miss问题小的多。

劣处

  直方图算法不能找到很精确的分割点，因为它访问的是bins，但从实验结果来看，直方图算法的测试误差效果甚至更好。因为决策树对分割点的精确程度不太敏感，并且较“粗”的分割点也自带正则化的效果，再加上boosting算法本身就是弱分类器的集成。

  后续工作：对于GOSS，需要优化$a$和$b$的选择；对于EFB，需要优化处理更多的特征无论是否稀疏。

LightGBM的参数

  控制参数
  max_depth：树的最大深度。当模型过拟合时，可以考虑首先降低max_depth。
  min_data_in_leaf：叶子可能具有的最小记录数。默认是20，过拟合时使用。
  feature_fraction：例如为0.8时，意味着在每次迭代中随机选择80%的参数来构建树。boosting为random forest时使用。
  bagging_fraction：每次迭代时用的数据比例。用于加快训练速度和缓解过拟合。
  early_stopping_round：如果一次验证数据的一个度量在最近的early_stopping_round回合中没有提高，模型将停止训练。加速分析，减少过多迭代。
  lambda_l1：L1正则化，也称reg_alpha，0~1。
  lambda_l2：L2正则化，也称reg_lambda，0~1。
  main_gain_to_split：描述分裂的最小gain。控制树有用的分裂。
  max_cat_group：在group边界上找到分割点。当类别数量很多的时候，找分割点容易过拟合。
  cat_smooth：default=10，用于分类特征，降低噪声在分类特征中的影响，尤其是对数据很少的类别。
  
  核心参数
  boosting：default=gbdt，还有rf，dart，doss。可选参数比XGBoost中多。
  num_thread：指定线程的个数，数字设置成CPU内核数比线程数训练更快，并行学习不应该设置成全部线程，这反而使得训练速度不佳。
  application：学习目标和损失函数，default=regression。
    regression:
      regression_l2：L2 loss, alias=regression, mean_squared_error, mse
      regression_l1：L1 loss, alias=mean_absolute_error, mae
      huber：Huber loss
      fair：Fair loss
      possion：Possion regression
      quartile：Quartile regression
      quartile_l2：类似于quartile，但使用了L2 loss
    binary: binary log loss classification application
    multi-class: classification
      multiclass：softmax目标函数，应该设置好num_class
      multiclassova：One-vs-All，二分类目标函数，应该设置好mun_class
    cross-entropy: application，取值为[0,1]
      xentropy：目标函数为cross-entropy（同时有可选择的线性权重）,alias=cross_entropy
      xentlambda：替代参数化的cross-entropy，alias=cross_entropy_lambda
    lambdarank: lambdarank application
      在lambdarank任务中标签应该为int type，数值越大代表相关性越高（例如 0：bad，1：fair，2：good，3：perfect）
      label_gain：可以用来设置int标签的增益（权重）
  vaild：验证集选用，支持多验证集，以,分割
  learning_rate：梯度下降的步长，default=0.1，一般在0.05~0.2之间。
  num_leaves:default=31，这代表的是一棵树上的叶子树。
  device：default=cpu，options=cpu、gpu
    - 为树学习选择合适的设备，可以使用GPU来获得更快的学习速度。GPU默认使用32位浮点数来求和，也可以设置gpu_use_dp=tree来启用64位浮点数，但其训练速度更低；
    - 建议使用较小的max_bin（例如63）来获得更快的速度；
    参考相关指南构建GPU版本。
  
  度量参数
  metric：default={l2 for regression}，{binary_logloss for binary classification}，{ndcg for lambdarank}
    l1: absolute loss, alias=mean_absolute_error, mae
    l2: square loss, alias=mean_squared_error, mse
    l2_root: root square loss, alias=root_mean_squared_error, rmse
    quantile: Quantile regression
    huber: Huber loss
    fair: Fair loss
    possion Poisson regression
    ndcg: NDCG
    map: MAP
    auc: AUC
    binary_logloss: log loss
    binary_error: 样本: 0 的正确分类, 1 错误分类
    multi_logloss: mulit-class 损失日志分类
    multi_error: error rate for mulit-class 出错率分类
    xentropy: cross-entropy (与可选的线性权重), alias=cross_entropy
    xentlambda: “intensity-weighted” 交叉熵, alias=cross_entropy_lambda
    kldiv: Kullback-Leibler divergence, alias=kullback_leibler
    支持多指标，使用,分隔