量子计算入门学习笔记 （五 ——张量，量子比特）

大家好，欢迎来到量子计算的第四部分，如果您是第一次观看我的博客，如果您也是和我一样刚入门量子力学或是量子计算相关的学习，纠结于量子的抽象与晦涩难懂，那么本专栏（量子计算）一定是您的不二之选，学海本就苦，愿你有甜心，如果觉得博主写的有错误的直接在评论区留言，博主也是大一的一名程序狗，希望大家多多支持，点点赞，另外，本专题是每周一更或二更，有需要的小伙伴可以点点专注！

一 . 张量积相关性质

在上一篇博客中，我们已经为大家介绍了张量积的定义，运算法则以及一些注意点，这里我们为大家详细的给出一些主要性质，大家可以随便写几个复数矩阵来验证是否正确：

1. 对任何矢量 $|{\phi }_1⟩,|{\phi }_2⟩\in {\mathbf{H}}_1,|\psi ⟩\in {\mathbf{H}}_2$,有
   $$\left(|{\phi }_1⟩+|{\phi }_2⟩\right)\otimes |\psi ⟩=|{\phi }_1⟩\otimes |\psi ⟩+|{\phi }_2⟩\otimes |\psi ⟩$$
2. 对任何矢量 $|\phi ⟩\in {\mathbf{H}}_1,|{\psi }_1⟩,|{\psi }_2⟩\in {\mathbf{H}}_2$,有：
   $$|\phi ⟩\otimes \left(|{\psi }_1⟩+|{\psi }_2⟩\right)=|\phi ⟩\otimes |{\psi }_1⟩+|\phi ⟩\otimes |{\psi }_2⟩$$
3. 对任何矢量 $|{\phi }_1⟩,|{\phi }_2⟩\in {\mathbf{H}}_1,|{\psi }_1⟩,|{\psi }_2⟩\in {\mathbf{H}}_2$,有:
   $$\left(|{\phi }_1{\psi }_1⟩,|{\phi }_2{\psi }_2⟩\right)=\left(|{\phi }_1⟩,|{\phi }_2⟩\right)\left(|{\psi }_1⟩,|{\psi }_2⟩\right)=⟨{\phi }_1|{\psi }_1⟩⟨{\phi }_2|{\psi }_2⟩$$
4. 对任何矢量 $|{\phi }_1⟩,|{\phi }_2⟩\in {\mathbf{H}}_1,|{\psi }_1⟩,|{\psi }_2⟩\in {\mathbf{H}}_2$,有:
   $$\left(|{\phi }_1⟩\otimes |{\psi }_1⟩\right)\left(|{\phi }_2⟩\otimes |{\psi }_2⟩\right)=\left(|{\phi }_1⟩|{\phi }_2⟩\right)\otimes \left(|{\psi }_1⟩|{\psi }_2⟩\right)$$
5. 对任何矢量 $|\phi ⟩\in {\mathbf{H}}_1,|\psi ⟩\in {\mathbf{H}}_2$,以及$c\in C$ 有 :
   $$c(|\phi ⟩\otimes |\psi ⟩)=(c|\phi ⟩)\otimes |\psi ⟩=|\phi ⟩\otimes (c|\psi ⟩)$$

举两个实例帮助大家理解:
5. 如果$A=\left(\begin{array}{l}{a}_{11}{a}_{12}\\ a_{21}{a}_{22}\end{array}\right);I=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$那么$A\otimes I=\left[\begin{array}{cccccc}{a}_{11}& 0& 0& a_{12}& 0& 0\\ 0& a_{11}& 0& 0& a_{12}& 0\\ 0& 0& a_{11}& 0& 0& a_{12}\\ a_{21}& 0& 0& a_{22}& 0& 0\\ 0& a_{21}& 0& 0& a_{22}& 0\\ 0& 0& a_{21}& 0& 0& a_{22}\end{array}\right]$

6. 若 $|v⟩=\left[\begin{array}{c}{v}_1\\ v_2\end{array}\right],|w⟩=\left[\begin{array}{c}{w}_1\\ w_2\\ w_3\end{array}\right],$ 那么 $|v⟩\otimes |w⟩=\left[\begin{array}{c}{v}_1{w}_1\\ v_1{w}_2\\ v_1{w}_3\\ v_2{w}_1\\ v_2{w}_2\\ v_2{w}_3\end{array}\right]$
7. 结合上面两个例子我们看下面这个综合一点的：
   $$(A\otimes I)(|v⟩\otimes |w⟩)=\left[\begin{array}{cccccc}{a}_{11}& 0& 0& a_{12}& 0& 0\\ 0& a_{11}& 0& 0& a_{12}& 0\\ 0& 0& a_{11}& 0& 0& a_{12}\\ a_{21}& 0& 0& a_{22}& 0& 0\\ 0& a_{21}& 0& 0& a_{22}& 0\\ 0& 0& a_{21}& 0& 0& a_{22}\end{array}\right]\left[\begin{array}{c}{v}_1{w}_1\\ v_1{w}_2\\ v_1{w}_3\\ v_2{w}_1\\ v_2{w}_2\\ v_2{w}_3\end{array}\right]=\left(\begin{array}{c}\left(a_{11}{v}_1+a_{12}{v}_2\right)w_1\\ \left(a_{11}{v}_1+a_{12}{v}_2\right)w_2\\ \left(a_{11}{v}_1+a_{12}{v}_2\right)w_3\\ \left(a_{21}{v}_1+a_{22}{v}_2\right)w_1\\ \left(a_{21}{v}_1+a_{22}{v}_2\right)w_2\\ \left(a_{21}{v}_1+a_{22}{v}_2\right)w_3\end{array}\right)=(A|v⟩)\otimes |w⟩$$

动手算一算其实没有看上那么复杂！

二 . 量子比特

1. 介绍(回忆)

在我们本专栏的第一篇博客中就曾浅谈过量子比特的一些东西，这里的深入讨论也许会让你在量子世界中原本就模糊的视线中带来一丝清晰！

在经典信息的处理过程中，记述其信息的二进制储存单元称为经典比特(bit)，经典比特由电压的高低 0,1表示，对于量子信息而言，记述量子信息的储存单元为量子比特(qubit) ， 其中一个 qubit 的状态是一个二维复数空间的矢量，它的两个极化状态$|0⟩$ 和$|1⟩$ 分别对应经典状态中的 0 和 1！

qubit 的两个极化状态$|0⟩$ 和$|1⟩$ 是二维复数列向量，他们是一组归一化正交基底，所以，其模必为1，二者内积必为0！

我们前面就说过大部分情况下:
$$|0⟩=\left[\begin{array}{l}1\\ 0\end{array}\right],|1⟩=\left[\begin{array}{l}0\\ 1\end{array}\right]$$

这没有特别的规定，也可以这样：
$$|0⟩=\frac{1}{\sqrt{2}}\left[\begin{array}{l}1\\ 1\end{array}\right],|1⟩=\frac{1}{\sqrt{2}}\left[\begin{array}{l}1\\ -1\end{array}\right]$$
只要满足前面的规律都行，当然，我们的选择需要根据实际情况而定，这是依赖于实际信息的载体采用哪一类微观粒子（这里说一下，我们的博客为了方便 ，在没有特别说明的情况下，都采用第一种）！

若 $\alpha$ 与 $\beta$ 是一对任意的满足归一化的复数，则某量子态$|\phi ⟩$可以写成为：

$$|\phi ⟩=\alpha |0⟩+\beta |1⟩=\alpha \left[\begin{array}{l}1\\ 0\end{array}\right]+\beta \left[\begin{array}{l}0\\ 1\end{array}\right]=\left[\begin{array}{l}\alpha \\ \beta \end{array}\right]$$
其中，$|\alpha {|}^2+|\beta {|}^2=1$ 。注意一下，二维复向量$\left[\begin{array}{l}{a}_1\\ a_2\end{array}\right]$，和$\left[\begin{array}{l}{b}_1\\ b_2\end{array}\right]$ 的内积，可以表示为：$\left[\begin{array}{ll}{a}_1& a_2^{\ast }\end{array}\right]\left[\begin{array}{l}{b}_1\\ b_2\end{array}\right]=a_1^{\ast }{b}_1+a_2^{\ast }{b}_2$，其中这个“ * ”符号表示的是共轭复数！

2.量子比特的测定

OMG，终于到主题了，前面的介绍一大串都是回忆之前我们学习过的，已经是老生常谈了，但是为了每一位问的观众阅读的连贯性，上面也算是复习了！

对于经典比特来说，我们可以用仪器直接测量在某一时刻它是取0 还是 1！但是在量子中：$|\phi ⟩=\alpha |0⟩+\beta |1⟩$,通常状况下，我们不知道 $\alpha ,\beta$ 的具体值，况且我们必须要从量子比特中获取出与经典比特相类似的信息才能完成测定！

我们通过一个被称为是 “测量” 的 过程,我们可以将一个qubit 的状态以概率幅的形式转化为 bit 信息。转化过程大概如下：

• 概率 为 ${\left|⟨0|\phi ⟩\right|}^2$ 变化为： bit 0
• 概率 为 ${\left|⟨1|\phi ⟩\right|}^2$ 变化为： bit 1

这里需要我们先求出量子比特 $|\phi ⟩=\alpha |0⟩+\beta |1⟩$ 的两个内积结果：

$$\begin{array}{l}⟨0|\phi ⟩=\alpha ⟨0|0⟩+\beta ⟨0|1⟩=\alpha \\ ⟨1|\phi ⟩=\alpha ⟨1|0⟩+\beta ⟨1|1⟩=\beta \end{array}$$

总结来说就是： $|\phi ⟩$ 以概率为 ${\left|\alpha \right|}^2$ 取值 bit 0，以概率为 ${\left|\beta \right|}^2$ 取值 bit 1，特别的，当 $\alpha =1$ 的时候， $|\phi ⟩$ 取 0 的概率为1 ；当 $\beta =1$ 的时候， $|\phi ⟩$ 取 1 的概率为1 ；这样，理论上我们就将qubit 与经典的 bit 对应起来了！

也就是说，量子比特被检测之前一直处于介于 $|0⟩$ 和 $|1⟩$ 之间的一个连续态。而测量时，仅概率性的给出 0 或 1 作为测量结果!

当然了，我们目前所描述和计算的是以第一组正交基底为前提的，基底变了，虽然远离一样，但是还是会发生一些细微的变化！

这是以我们前面所说的第二种基底表示的：
$$\begin{array}{rl}|\phi ⟩& =\frac{\alpha +\beta }{2}\left[\begin{array}{l}1\\ 1\end{array}\right]+\frac{\alpha -\beta }{2}\left[\begin{array}{c}1\\ -1\end{array}\right]\\ & =\frac{\alpha +\beta }{\sqrt{2}}|0⟩+\frac{\alpha -\beta }{\sqrt{2}}|1⟩\end{array}$$

这个时候以概率幅转化的结果有点不一样：

• 取 bit 0 概率为：$\frac{|\alpha +\beta {|}^2}{2}$
• 取 bit 1 概率为：$\frac{|\alpha -\beta {|}^2}{2}$

在这里要注意，如果即使是一个量子态基底选取不同的话，返回每个bit 值的 概率有可能是不一样的！

3 . 量子比特的另一种表现形式

除了我们上述介绍的最简单明了的量子比特表示方法，还有一种更加直观的表示方法，也称为 几何表示 ！
因为 $|\phi ⟩=\alpha |0⟩+\beta |1⟩$ ，$|\alpha {|}^2+|\beta {|}^2=1$，所以可以设：
$$\alpha =\cos \frac{\theta }{2}{e}^{i\delta },\beta =\sin \frac{\theta }{2}{e}^{i(\delta +\varphi )}$$
代入你就可以得到：
$$|\psi ⟩=\cos \frac{\theta }{2}{e}^{i\delta }|0⟩+\sin \frac{\theta }{2}{e}^{i(\delta +\varphi )}|1⟩=e^{i\delta }\left(\cos \frac{\theta }{2}|0⟩+\sin \frac{\theta }{2}{e}^{i\varphi }|1⟩\right)$$

这里的 $\theta ,\varphi ,\delta$都是实数，而 $i$ 是虚数，因为 $e^{i\delta }$ 称作共同相位（global phase），因为对$|0⟩$ 和 $|1⟩$ 都一样影响，而在实验上测量不出来，故可以将之舍弃不看!

所以，可以简写为:
$$|\psi ⟩=\cos \frac{\theta }{2}|0⟩+\sin \frac{\theta }{2}{e}^{i\varphi }|1⟩$$
这里的$\theta ,\varphi$ 定义了单位三维球面上的一个点！这个球被称为Bloch球，如图：
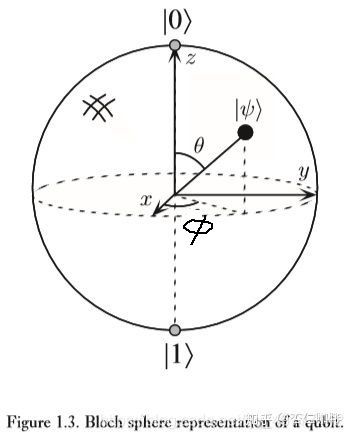和前面那个图一模一样！这里的Bloch球可谓是高深莫测！肯定会有小伙伴会问这为啥直接那样设$\alpha ,\beta$的值，很抱歉，博主也在探索之中，在后面的博客可能会问大家带来详细的数学推导！我们现在介绍的是 纯态，在bloch 球的表面，其实这个球内的每一个点还能映射到量子的混合态!除此之外还可以在这个球内完成本征谱分解 有感兴趣的小伙伴可以去学学！

好的，本次博客学习就到这里了，喜欢的话不要忘记点点关注，谢谢大家！